Сколько лет математике как науке

Сколько лет математике как науке? История математики, ее развитие и важность в наши дни. Узнайте, как математика стала одной из основных наук и какие достижения она принесла человечеству.

Математика — это одна из старейших наук, которая изучает структуру, свойства и отношения чисел, пространства и фигур. Впервые как самостоятельная дисциплина она появилась в Древней Греции около 2500 лет назад. Но ее история насчитывает гораздо больше времени.

Уже в древних цивилизациях, таких как Месопотамия и Египет, люди использовали математические знания для решения практических задач, связанных с торговлей, строительством и земледелием. Однако, именно греки сделали первый серьезный шаг к систематизации и развитию математики как науки.

Знаменитые греческие математики, такие как Пифагор, Евклид, Архимед и другие, внесли огромный вклад в развитие математического мышления и создали основу для многих современных математических понятий и методов. Благодаря их трудам математика стала признанной наукой, которая способна решать сложные проблемы и открывать новые горизонты познания.

Математика — это язык, который позволяет нам понять и описать законы природы, прогнозировать будущие события и разрабатывать новые технологии. Она играет важную роль в науке, инженерии, экономике и других областях человеческой деятельности.

С течением времени, математика продолжала развиваться и расширять свои области применения. С появлением компьютеров и развитием информационных технологий, математические методы стали неотъемлемой частью многих научных и технических исследований. Сегодня математика занимает центральное место во многих современных научных дисциплинах и является основой для многих технических и технологических инноваций.

История математики: от древности до средних веков

В Древней Греции математика начала развиваться как самостоятельная наука. Здесь были сформулированы основные математические понятия и аксиомы, а также разработаны методы решения различных математических задач. Великие ученые, такие как Пифагор, Евклид, Архимед и Аполлоний, внесли значительный вклад в развитие математики.

В период средних веков развитие математики сильно замедлилось из-за политических, религиозных и социальных причин. Однако в этот период восточные ученые, такие как арабские математики, продолжали заниматься математикой и внесли свой вклад в развитие алгебры, геометрии и тригонометрии.

Средние века также ознаменовались возрождением науки и искусства в Западной Европе, что привело к новому витку развития математики. Математические идеи и методы, разработанные в этот период, в значительной степени определили современную математику. Великие математики, такие как Леонардо Пизанский (Фибоначчи), Николай Коперник, Рене Декарт и Пьер де Ферма, внесли свой вклад в различные области математики, включая алгебру, геометрию и анализ.

Таким образом, история математики от древности до средних веков является периодом развития и становления этой науки, который существенно повлиял на ее дальнейшее развитие.

Возникновение математики как науки в Древней Греции

Математика, как наука, начала свое развитие в Древней Греции. Великие мыслители и философы этого времени играли важную роль в формировании математической науки и ее основных принципов.

Одним из первых великих математиков Древней Греции был Пифагор, который создал школу, изучавшую геометрию и арифметику. Его учение о числах, названное пифагоризмом, считалось священным и духовным. Пифагорейские математики разработали основные принципы арифметики, геометрии и музыки.

Однако наибольший вклад в развитие математики сделал Евклид, который создал свой знаменитый труд «Начала», известный также как «Евклидовы начала». В этой книге он систематизировал и упорядочил математические знания своего времени. Евклид формализовал понятия и введение аксиомы и доказательства стали основой математического рассуждения.

Другим великим математиком Древней Греции был Архимед. Он сделал значительные открытия в области геометрии и механики. Архимед известен своими работыми по определению площади и объема геометрических фигур, а также закону о силе архимедовой. Он использовал методы исчисления, которые помогли ему решать сложные задачи.

Таким образом, благодаря вкладу Пифагора, Евклида, Архимеда и других древнегреческих математиков, математика стала наукой с строгими правилами и доказательствами. Их работы исследовались и развивались вплоть до современности, и считается, что древнегреческая математика положила основы для многих современных математических теорий и методов.

Развитие математических идей в Индии и Исламском мире

Математика имеет долгую и богатую историю в Индии и Исламском мире. Оба региона внесли значительный вклад в развитие математических идей, которые оказали влияние на мировую науку.

В Индии, развитие математики началось задолго до нашей эры. Древние индийские математики создали систему чисел, которая стала основой для развития арифметики и алгебры. Они также разработали методы решения уравнений, включая квадратные и кубические уравнения.

В Исламском мире математика начала развиваться в 8 веке. Исламские математики внесли важный вклад в развитие алгебры, геометрии и тригонометрии. Они также создали систему чисел, которая стала известна как арабские цифры и стала широко использоваться по всему миру.

Исламские математики также продвинулись в области алгебры, разработав новые методы решения уравнений, включая квадратные и кубические уравнения. Они также внесли вклад в развитие теории чисел и теории вероятностей.

Оба региона сыграли важную роль в сохранении и распространении математических знаний. Индийские и исламские математики переводили и комментировали древние греческие тексты, что помогло сохранить эти знания для будущих поколений.

Развитие математических идей в Индии и Исламском мире имеет глубокое значение для современной математики. Они стали основой для многих современных математических концепций и методов и продолжают вдохновлять ученых по всему миру.

Ренессанс и научная революция: новые подходы в математике

Одним из ключевых событий Ренессанса было восстановление и распространение античных математических знаний. Великие математики и ученые такие, как Архимед, Евклид и Птолемей, стали источником вдохновения для математиков Ренессанса. Произведения этих ученых были переизданы и переведены на различные европейские языки, что позволило математикам получить доступ к древним знаниям и начать их изучение и развитие.

Одним из важнейших достижений математиков Ренессанса было изобретение алгебры. Математики, такие как Франсуа Виет, Рене Декарт и Николай Иванович Лобачевский, разработали новые символы и методы для работы с алгебраическими уравнениями. Изобретение алгебры открыло новые возможности для решения сложных математических задач и стало основой для развития других областей математики, таких как анализ и геометрия.

Вместе с развитием алгебры, математики Ренессанса также начали активно исследовать геометрию. Одним из наиболее значимых достижений в этой области стало открытие новых геометрических форм, таких как эллипс, гипербола и парабола. Эти формы были исследованы и описаны такими математиками, как Жан Батиста Виет, Иоганн Кеплер и Рене Декарт. Открытие новых геометрических форм позволило математикам пересмотреть и расширить свои знания о пространстве и формах.

Научная революция, которая произошла в 16-17 веках, также оказала значительное влияние на развитие математики. Одним из ключевых факторов научной революции было отказ от догматического подхода и принятие эмпирического метода исследования. Математики стали все более активно применять экспериментальные методы и математическое моделирование для изучения физических явлений и разработки новых математических теорий.

Ренессанс и научная революция внесли значительный вклад в развитие математики как науки. Благодаря открытию новых подходов и разработке новых методов, математики Ренессанса и ученые научной революции смогли расширить границы математического знания и сделать важные открытия, которые оказали влияние на многие области науки и техники.

Открытие бесконечности и новые математические области

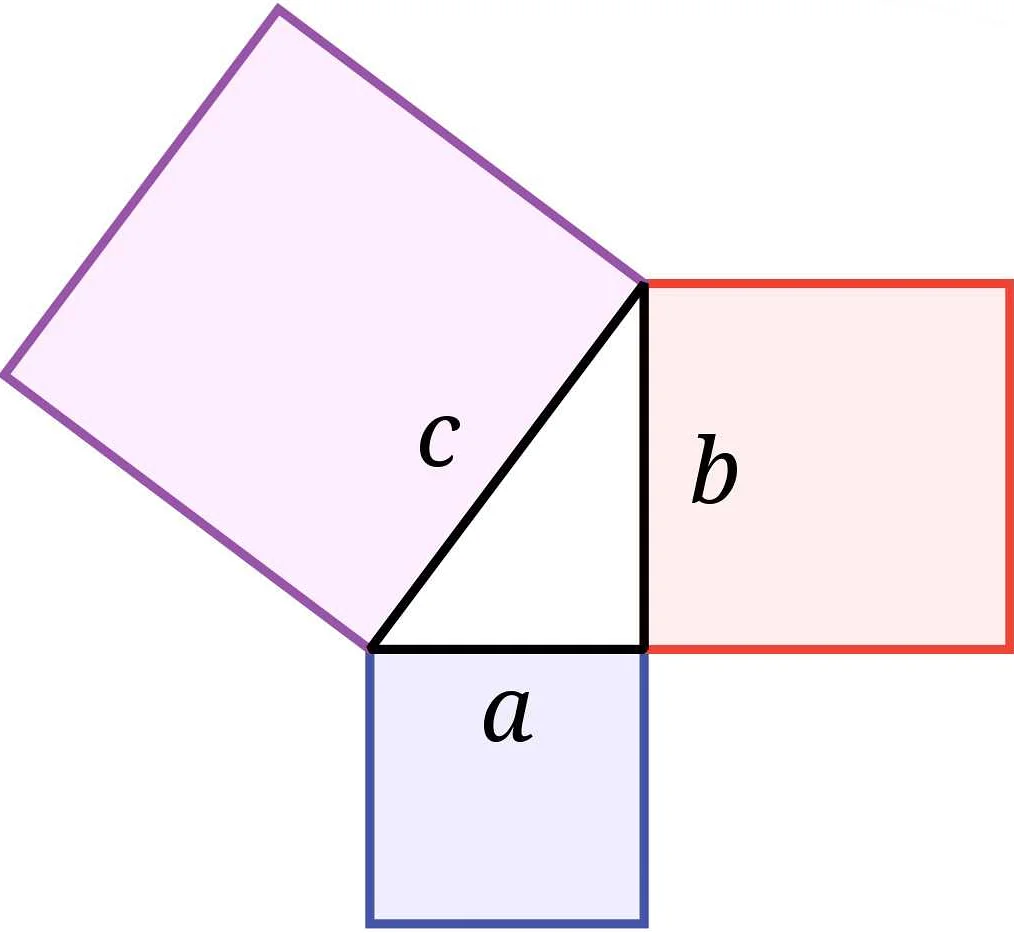
Открытие бесконечности стало одним из ключевых моментов в развитии математики. Первоначально идея о бесконечности возникла в древней Греции, где математики, такие как Зенон и Парменид, начали размышлять о парадоксах, связанных с бесконечностью.

В дальнейшем, математики разработали строгую формализацию понятия бесконечности. В 19 веке Кантор ввел понятие множества, которое стало основой для дальнейшего изучения бесконечности. Он доказал, что существуют разные типы бесконечности и различные степени бесконечности.

Открытие бесконечности имело огромное влияние на развитие математических областей. Новые исследования возникли в области математического анализа, теории множеств, теории вероятностей и других дисциплин.

Например, математический анализ стал изучать бесконечные ряды и пределы функций, что позволило решать сложные задачи в физике и инженерии. Теория множеств использовалась для формализации математических концепций и разработки логических основ математики. Теория вероятностей была развита для моделирования случайных событий и применения в статистике.

Открытие бесконечности также привело к возникновению новых математических областей, таких как теория категорий, математическая логика и комплексный анализ. Эти области исследуют различные аспекты бесконечности и имеют широкое применение в различных науках и инженерии.

Математические области, связанные с бесконечностью:Примеры применения:

Теория категорий	Функциональное программирование, теория баз данных
Математическая логика	Разработка компьютерных алгоритмов, искусственный интеллект
Комплексный анализ	Электротехника, квантовая физика

Математика в Новое время: приложения и прорывы

В Новое время математика стала невероятно полезной и практической наукой, нашла свое применение во множестве областей. Она стала неотъемлемой частью развития техники, физики, экономики и других наук.

Одной из важнейших областей применения математики стало исследование физических явлений. С помощью математических методов были разработаны теории относительности, квантовой механики, электродинамики и многих других. Математика позволяет описывать и объяснять сложные физические процессы, а также предсказывать результаты экспериментов.

В экономике математика стала неотъемлемым инструментом для анализа рынков, определения оптимальных стратегий, моделирования финансовых инструментов и прогнозирования экономической ситуации. Математические модели позволяют выявлять закономерности и тенденции в экономических данных, а также предсказывать будущие события и принимать обоснованные решения.

Математика также нашла свое применение в компьютерных науках и информационных технологиях. Она является основой для разработки алгоритмов, шифров и методов обработки данных. Математические методы позволяют решать сложные задачи в области искусственного интеллекта, машинного обучения, компьютерной графики и других смежных областях.

Математика продолжает развиваться и находить новые области применения. Современные математические прорывы открывают новые возможности в области криптографии, больших данных, оптимизации и многих других.

Математическая логика и основания математики

Основания математики — это область, связанная с формализацией и аксиоматическим представлением математических теорий. Она стремится дать строгую и непротиворечивую основу для всей математики. Ее целью является определение аксиоматических систем, которые могут быть использованы для вывода всех математических утверждений.

Одной из важных теорий, связанных с математической логикой и основаниями математики, является теория множеств. Она изучает свойства и отношения множеств, определяет операции над множествами и исследует различные аксиоматические системы для математических утверждений, основанных на множествах.

Математическая логика и основания математики играют ключевую роль в развитии математики и ее приложений. Они позволяют математикам формализовать и проверять математические доказательства, а также создавать новые математические теории и методы. Без математической логики и оснований математики развитие математики было бы гораздо сложнее и менее систематичным.

Современная математика: открытия и тенденции развития

Одним из самых значимых открытий последних лет является доказательство Перельманом гипотезы Пуанкаре. Эта гипотеза была поставлена в 1904 году и являлась одной из семи проблем тысячелетия, предложенных Международным математическим союзом. Доказательство Перельмана открыло новые возможности для изучения топологии и геометрии многообразий.

Также стоит отметить развитие теории графов и компьютерной математики. С появлением современных компьютеров и вычислительных технологий, математики получили новые инструменты для решения сложных задач. Компьютерные методы позволяют проводить эксперименты, анализировать большие объемы данных и находить новые закономерности.

Еще одной важной тенденцией развития современной математики является интеграция с другими научными областями. Математика становится неотъемлемой частью физики, биологии, экономики и других дисциплин. Взаимодействие математиков с учеными из разных областей позволяет находить новые решения и применять математические методы для решения актуальных проблем.

НазваниеОписаниеГод открытия

Теория множеств	Изучает свойства и отношения множеств	1874
Теория вероятностей	Изучает случайные события и вероятности их наступления	1654
Теория чисел	Изучает свойства и отношения натуральных чисел	Древнейшие времена

Современная математика продолжает активно развиваться и открывать новые направления и подходы. Открытия и достижения математиков имеют важное значение не только для науки, но и для практического применения в разных областях жизни.

Вопрос-ответ:

Как долго математика существует как наука?

Математика как наука существует уже более 2500 лет. Ее история начинается с древнейших цивилизаций, таких как Месопотамия, Египет и Греция.

Как математика развивалась со временем?

Со временем математика продолжала развиваться и совершенствоваться. Были созданы новые математические методы, открыты новые теоремы и принципы.

Какие важные открытия были сделаны в истории математики?

В истории математики было сделано множество важных открытий. Например, открытие бесконечности, развитие алгебры и геометрии, открытие дифференциального и интегрального исчисления, и многое другое.

Как математика влияет на современное общество?

Математика играет важную роль в современном обществе. Она применяется в науке, технологиях, экономике, финансах, медицине и многих других областях. Без математики невозможно представить себе развитие современного мира.

Какие перспективы развития математики в будущем?

Математика по-прежнему будет развиваться и прогрессировать в будущем. С развитием компьютерных технологий и искусственного интеллекта, математические методы будут все более востребованы и применяются во многих сферах жизни.

Видео по теме: