Что такое теорема в математике
Содержимое
- 1 Что такое теорема в математике
Теорема в математике — это утверждение, которое было доказано и является истинным для всех условий, указанных в теореме. Она играет важную роль в развитии математики, позволяя устанавливать новые связи и закономерности между математическими объектами и явлениями. Теоремы широко используются во всех областях математики и имеют значительное практическое применение.
Математика — это наука, которая изучает структуру, пространство, количество и изменения. В основе математики лежат аксиомы, определения и теоремы. Теорема — это утверждение, которое может быть доказано с использованием логических рассуждений и уже доказанных утверждений. Она является одним из основных инструментов в математике и играет важную роль в развитии этой науки.
Одной из самых известных теорем в истории математики является теорема Пифагора. Она гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это утверждение было доказано греческим математиком Пифагором и до сих пор используется в решении различных задач и проблем.
«Теоремы — это некий фундаментальный камень математики. Они являются основой для построения сложных математических конструкций и решения различных задач. Без теорем математика не могла бы существовать в своем современном виде.»
Теоремы могут быть сформулированы на различных областях математики, таких как алгебра, геометрия, теория вероятностей и другие. Они служат основой для построения математических моделей и решения сложных проблем. Доказательства теорем требуют строгой логики и систематического подхода, и могут быть представлены в виде формальных математических доказательств или через устные или письменные объяснения.
Определение теоремы в математике
Теоремы являются фундаментальными понятиями в математике и играют важную роль в развитии и установлении новых математических знаний. Они позволяют строить математические модели, решать сложные проблемы и выводить новые результаты на основе существующих знаний.
Доказательство теоремы — это логическое рассуждение, которое представляет собой последовательность логических шагов, следующих из уже установленных доказанных утверждений. Доказательство должно быть строгим, непротиворечивым и убедительным, чтобы убедить других математиков в справедливости утверждения.
Теоремы могут быть разделены на различные области математики, такие как алгебра, геометрия, теория чисел, математический анализ и другие. Они могут быть простыми и очевидными или сложными и требующими длительных и сложных доказательств.
Примером теоремы может служить теорема Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Эта теорема имеет множество доказательств и является одной из основных теорем в геометрии.
Основные принципы теоремы
Теорема в математике представляет собой утверждение, которое может быть доказано с использованием аксиом, определений и ранее доказанных утверждений. Основные принципы теоремы обычно включают:
- Условие: это начальное утверждение, которое должно быть выполнено для применения теоремы. Условие может быть выражено в форме уравнения, неравенства или другого математического выражения.
- Тезис: это утверждение, которое будет доказано с использованием условия. Тезис должен быть строго логическим следствием из условия и других математических фактов.
- Доказательство: это логическое объяснение, которое демонстрирует, как тезис следует из условия и других фактов. Доказательство должно быть четким, последовательным и логически верным.
Основные принципы теоремы позволяют математикам формулировать и доказывать новые утверждения, основываясь на уже известных фактах. Они играют важную роль в развитии математики и применяются во многих ее областях, таких как алгебра, геометрия, анализ и теория вероятностей.
Примеры теорем в математике
В математике существует множество важных и известных теорем, которые играют важную роль в различных областях науки. Вот несколько примеров таких теорем:
Теорема Пифагора: Эта теорема утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. То есть, если a и b — длины катетов, а c — длина гипотенузы, то справедливо равенство a^2 + b^2 = c^2.
Теорема Ферма: Эта теорема была сформулирована Пьером Ферма в 17 веке и доказана только в 20 веке. Она утверждает, что для любого натурального числа n > 2 уравнение x^n + y^n = z^n не имеет целочисленных решений x, y, z.
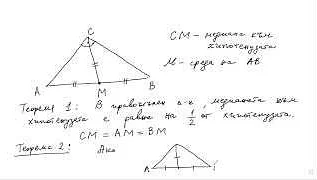
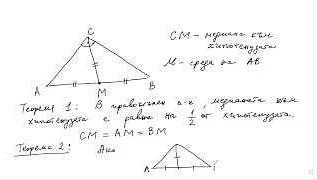
Теорема Фалеса: Эта теорема устанавливает, что в треугольнике, проведенная из вершины, параллельная одной из сторон, делит другие две стороны пропорционально. Или другими словами, если AB и CD — параллельные отрезки, то соотношение AC/AD = BC/BD.
Теорема Эйлера: Эта теорема связывает в себе понятия чисел, функций и графов. Она утверждает, что в связном графе число вершин минус число ребер плюс число граней равно 2. Или по формуле E — V + F = 2, где E — число ребер, V — число вершин, F — число граней.
Это лишь небольшой список из множества теорем, которые существуют в математике. Каждая из них имеет свои особенности и применения в различных областях науки и практики.
Классификация теорем
В математике теоремы могут быть классифицированы по различным признакам. Вот некоторые основные классификации теорем:
КлассификацияОписаниеПримеры
| По содержанию | Теоремы, связанные с определенной областью математики или конкретным математическим объектом. | Теорема Пифагора |
| По виду доказательства | Теоремы, которые могут быть доказаны различными методами, такими как аксиоматическое доказательство, индукция, от противного и др. | Теорема Ферма |
| По значимости | Теоремы, которые имеют особую важность в математике и широкое применение. | Теорема Фундаментальная теорема арифметики |
Классификация теорем помогает упорядочить знания в математике и облегчает их изучение и применение. Каждый тип теоремы имеет свои особенности и требует определенного подхода при их изучении и доказательстве. Важно понимать, что классификация теорем не является исчерпывающей и новые классификации могут появляться с развитием математики.
Доказательство теоремы

Доказательство теоремы состоит из нескольких шагов, каждый из которых строго следует из предыдущего. Обычно оно начинается с формулировки утверждения, которое будет доказываться, и предварительного описания используемых понятий и определений.
Далее следует логический вывод, в котором используются аксиомы, определения и ранее доказанные теоремы. Процесс доказательства может включать применение различных методов, таких как индукция, от противного, математическая интуиция и другие.
После вывода основной части доказательства часто приводятся заключительные рассуждения, подводящие итог и устанавливающие связь с ранее известными результатами. Это позволяет убедиться в корректности доказательства и правильности сделанных выводов.
Важно отметить, что доказательство теоремы должно быть строго и четко структурировано, чтобы быть понятным и убедительным для других математиков. Также, кроме формального доказательства, важна и интуитивная наглядность, которая помогает понять суть и идею доказательства.
Доказательство теоремы является ключевым элементом математической науки, поскольку оно позволяет устанавливать новые факты и открывать новые области знаний. Оно требует логической стройности, тщательного анализа и творческого мышления.
Значение теоремы в математике
Значение теоремы в математике заключается в том, что она является строгим математическим результатом, который можно использовать как основу для дальнейших выводов и развития теории. Теоремы позволяют устанавливать законы и отношения между математическими объектами и явлениями, что позволяет строить математические модели и прогнозировать результаты.
Теоремы также играют важную роль в образовании и обучении математике. Они позволяют студентам понять и освоить основные концепции и методы математики, а также развить логическое и аналитическое мышление.
Примеры теоремОписание
| Теорема Пифагора | Утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. |
| Теорема Ферма | Утверждает, что для любого натурального числа n>2 не существует таких целых чисел x, y и z, что x^n + y^n = z^n. |
| Теорема Фундаментальная теорема алгебры | Утверждает, что каждый многочлен с комплексными коэффициентами имеет хотя бы один комплексный корень. |
Видео по теме:
Вопрос-ответ:
Что такое теорема в математике?
Теорема в математике — это утверждение, которое было доказано и имеет строгие математические основания. Теоремы являются основой математического знания и позволяют строить новые выводы и развивать науку.
Каковы основные принципы теорем в математике?
Основные принципы теорем в математике — это строгое математическое доказательство и соблюдение логических законов. Доказательство теоремы должно быть непротиворечивым, последовательным и основываться на уже установленных математических фактах.
Какие примеры теорем можно привести?
Примеры теорем в математике многочисленны. Некоторые из них: теорема Пифагора, которая устанавливает соотношение между длинами сторон прямоугольного треугольника; теорема Ферма, которая утверждает, что для уравнения x^n + y^n = z^n, где n > 2, не существует натуральных чисел x, y и z; теорема Фалеса, которая устанавливает пропорциональность сторон в треугольнике, образованном прямыми, параллельными одной стороне треугольника.
Каким образом доказывается теорема в математике?
Доказательство теоремы в математике является основной частью математической работы. Доказательство строится на основе существующих математических понятий, определений и ранее доказанных теорем. Доказательство должно быть строгое, логичное и непротиворечивое, чтобы полностью подтвердить утверждение теоремы.
Какова роль теорем в математике?
Теоремы играют важную роль в математике. Они позволяют формализовать и систематизировать знания, а также развивать новые идеи и методы. Теоремы являются основой для построения математической теории, и без них не было бы возможности развивать науку и применять ее в различных областях.
Известные теоремы
1. Теорема Ферма
Теорема Ферма, или Великая теорема Ферма, является одной из самых известных и долго нерешенных проблем в математике. Ферма сформулировал эту теорему в 1637 году, утверждая, что уравнение x^n + y^n = z^n не имеет целочисленных решений, если n больше 2. Это утверждение стало известно как «Великая теорема Ферма». Доказательство этой теоремы было найдено только в 1994 году энглийским математиком Эндрю Уайлсом.
2. Теорема Пифагора
Теорема Пифагора, также известная как Пифагорова теорема, утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Формула теоремы Пифагора выглядит следующим образом: a^2 + b^2 = c^2, где a и b — длины катетов, а c — длина гипотенузы.
3. Теорема Фалеса
Теорема Фалеса утверждает, что если на сторонах треугольника построить отрезки, параллельные одной из сторон, то эти отрезки делят другие две стороны в пропорции. Формально, если точка D на стороне AB делит ее в отношении AD/DB, а точка E на стороне AC делит ее в отношении AE/EC, то отрезки DE и BC параллельны и делят сторону AC в одинаковом отношении.
Роль теорем в научных исследованиях
Теоремы играют важную роль в научных исследованиях, особенно в математике. Они представляют собой утверждения, которые доказаны истинными на основе логического рассуждения и ряда предположений.
Теоремы являются основополагающими элементами математического знания и используются для построения более сложных и общих теорий. Они служат основой для доказательства других математических утверждений и формулирования новых гипотез.
Теоремы также играют важную роль в научных исследованиях в других областях знания. Например, в физике, теоремы могут использоваться для формулировки фундаментальных законов и принципов, которые описывают природу и ее взаимодействие. В экономике, теоремы могут быть использованы для моделирования и анализа сложных экономических систем.
Теоремы также играют важную роль в научных исследованиях в области информатики и компьютерных наук. Они могут использоваться для доказательства правильности алгоритмов и программ, а также для разработки новых методов и подходов к решению сложных задач.
Важно отметить, что теоремы не являются просто математическими фактами или утверждениями, они имеют глубокое понимание и обоснование. Их доказательства требуют строгой логики, а также использования математических методов и инструментов.
Таким образом, теоремы играют важную роль в научных исследованиях, обеспечивая основу для развития математики и других областей науки. Они позволяют нам понять и объяснить законы и принципы, лежащие в основе природы и нашего мира.


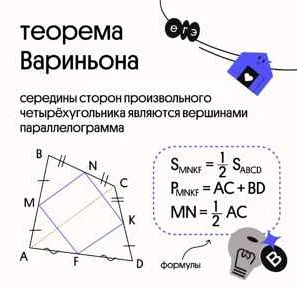

Очень интересная статья! Я всегда задавался вопросом, что такое теорема в математике. Теперь, после прочтения, я стал гораздо более осведомленным на эту тему. Определение теоремы в математике, данное в статье, помогло мне понять, что это математическое утверждение, которое доказывается на основе логики и ранее доказанных результатов. Примеры теорем, приведенные в статье, впечатляют своей сложностью и глубиной. Это подталкивает меня задуматься о мощи и значимости математики. Я осознал, что теоремы являются основными строительными блоками математического знания, и без них наука о числах была бы несостоятельной. Кроме того, статья объяснила мне основные принципы доказательства теоремы, такие как аксиомы, логические выводы и формальные системы. Я даже начал понимать, как математики приходят к своим открытиям и находят новые теоремы. В целом, статья очень понятно и интересно изложена, и она позволила мне более глубоко погрузиться в мир математики. Я остался восхищен и заинтересован в изучении этой науки. Большое спасибо за информативный материал!