Что такое состав числа в математике 1 класс

Состав числа в математике 1 класса — это разложение числа на сумму его составляющих, которые образуют это число. В данной статье рассматривается, как разложить число на единицы и десятки, и какие понятия с ними связаны.

Математика — наука, изучающая числа и их свойства. Состав числа — одно из основных понятий, которое помогает понять, из каких частей состоит число и сколько этих частей. Для первоклассников это понятие является важным, так как оно лежит в основе дальнейшего изучения математики.

Число можно представить как сумму или разность нескольких составляющих его частей. Например, число 7 можно разложить на две составляющие — число 5 и число 2. Это означает, что 7 можно получить, складывая 5 и 2. Таким образом, состав числа позволяет нам легко определить, какие числа нужно сложить или вычесть, чтобы получить данное число.

Для лучшего понимания состава числа, можно использовать практические примеры. Например, если у нас есть 8 яблок и мы отдаем 3, то остается 5. В этом примере число 8 разбивается на две составляющие — число 3 и число 5. Таким образом, состав числа помогает нам легко понять, сколько осталось яблок после того, как мы отдали некоторое количество.

Понимание состава числа является важным навыком, который помогает детям развивать математическое мышление и логику. Осознанный подход к изучению чисел позволяет лучше понимать мир вокруг и решать различные задачи.

Что такое состав числа?

Состав числа является важным понятием в математике и помогает ученикам лучше понять структуру чисел и их связь друг с другом. Знание состава числа помогает в решении математических задач и развивает навыки анализа и логического мышления.

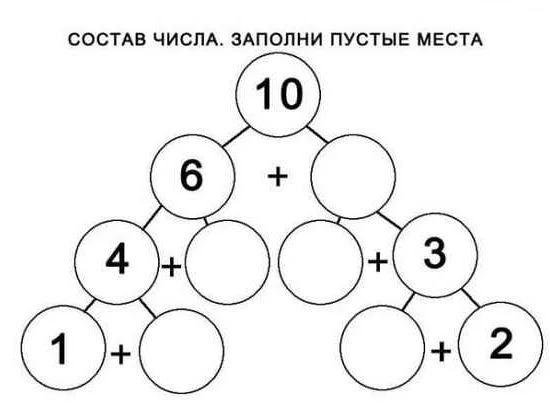
Состав числа может быть представлен различными способами. Например, число 10 можно разложить на сумму чисел 4 и 6, или на сумму чисел 7 и 3. Важно помнить, что состав числа не всегда единственный и может иметь несколько вариантов.

Например:

• Число 12 можно разложить на сумму чисел 8 и 4, или на сумму чисел 5 и 7.
• Число 15 можно разложить на сумму чисел 9 и 6, или на сумму чисел 7 и 8.

Понимание состава числа помогает ученикам узнавать числа, записанные в различных формах. Например, число 9 можно представить как сумму чисел 5 и 4, или как разность чисел 13 и 4.

Изучение состава числа является одним из основных этапов в изучении математики для первого класса. Ученикам предлагается решать задачи, находить различные способы состава чисел и оттачивать навыки анализа и логического мышления.

Определение и основные понятия

Состав числа — это способ представления числа в виде суммы или комбинации других чисел. Когда мы разбиваем число на составляющие его части, мы можем лучше понять его структуру и свойства.

Цифра — это символ, который используется для обозначения числа. В десятичной системе числения мы используем десять цифр от 0 до 9. Цифры могут быть использованы для создания различных чисел путем изменения их порядка и комбинирования.

Десятичное число — это число, записанное в десятичной системе счисления. Оно состоит из цифр от 0 до 9 и может содержать десятичную запятую, которая отделяет целую часть числа от дробной.

Разряд числа — это позиция, которую занимает цифра в числе. В десятичной системе счисления у нас есть разряды от единицы до бесконечности. Каждый разряд имеет свое значение, которое зависит от его позиции.

Единицы — это цифры, которые находятся в самом правом разряде числа. Они представлены значением от 0 до 9 и обозначают количество единичных предметов или явлений.

Десятки — это цифры, которые находятся в разряде десятков числа. Они представлены значением от 0 до 9, умноженным на 10, и обозначают количество десятичных предметов или явлений.

Сотни — это цифры, которые находятся в разряде сотен числа. Они представлены значением от 0 до 9, умноженным на 100, и обозначают количество сотен предметов или явлений.

Тысячи — это цифры, которые находятся в разряде тысяч числа. Они представлены значением от 0 до 9, умноженным на 1000, и обозначают количество тысячных предметов или явлений.

Разряды чисел — это порядковая система, которая используется для организации чисел. Каждый разряд представляет определенный порядок и имеет свое значение. Например, в десятичной системе разряды идут от правого к левому, увеличиваясь в десять раз с каждым разрядом.

Простые и составные числа

Простые числа — это числа, которые имеют только два делителя: 1 и само число. Примеры простых чисел: 2, 3, 5, 7, 11 и т.д. Простые числа не могут быть разложены на произведение других чисел, кроме как умножением на 1 и само число.

Составные числа — это числа, которые имеют больше двух делителей. То есть, они могут быть разложены на произведение простых чисел. Примеры составных чисел: 4, 6, 8, 9, 10 и т.д. Составные числа можно представить в виде произведения простых чисел. Например, число 6 можно разложить на произведение 2 * 3.

Знание простых и составных чисел помогает в понимании различных аспектов математики, включая факторизацию, нахождение наибольшего общего делителя и другие математические операции.

Важно понимать разницу между простыми и составными числами, чтобы лучше разбираться в различных математических концепциях и задачах.

Как разложить число на множители?

Для начала, проверьте, делится ли число на 2. Если да, то 2 является одним из множителей. Затем, проверьте, делится ли число на 3. Если да, то 3 является еще одним множителем. Продолжайте проверять делится ли число на другие простые числа, включая 5, 7, 11 и т. д., до тех пор, пока число не станет равным 1.

Например, для числа 24 мы начинаем с деления на 2, и получаем: 24 ÷ 2 = 12. Затем делим 12 на 2 и получаем: 12 ÷ 2 = 6. Далее делим 6 на 2 и получаем: 6 ÷ 2 = 3. Таким образом, число 24 разлагается на множители: 2 × 2 × 2 × 3 = 24.

Разложение числа на множители позволяет нам легко описывать число, а также проводить операции с ними. Например, разложение числа на множители использовать для упрощения дробей или нахождения наибольшего общего делителя.

Важно понимать, что каждое число имеет только одно разложение на множители. Дополнительные множители можно добавить, если в разложении этого числа используются одни и те же простые числа несколько раз.

Умение разлагать числа на множители позволяет нам лучше понимать и работать с числами, а также решать различные задачи в математике.

Понятие множителя

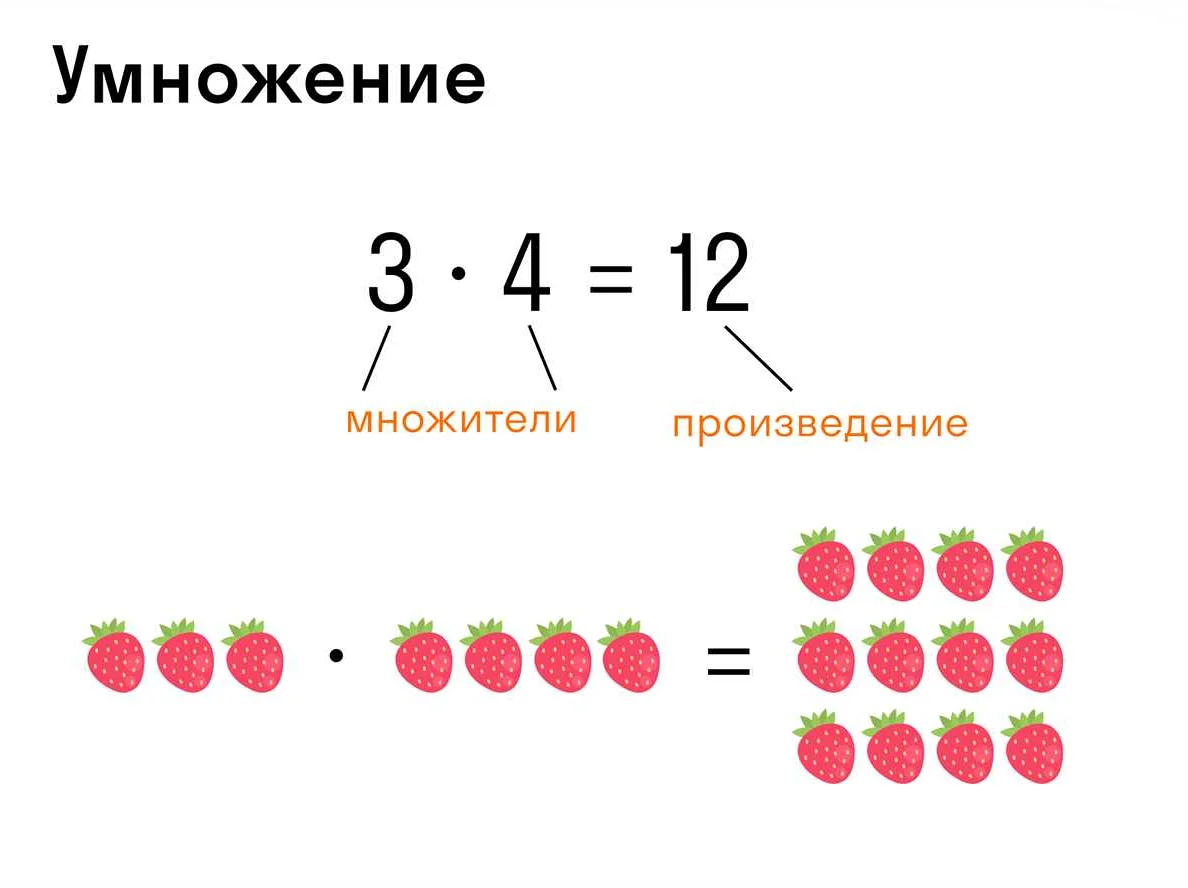
Например, в выражении 3 * 4 = 12, число 3 и число 4 являются множителями. Здесь число 3 определяет количество групп, а число 4 определяет количество элементов в каждой группе. Результатом умножения является произведение чисел, в данном случае 12.

Множитель может быть любым числом, включая нуль и отрицательные числа. Например, в выражении 2 * (-5) = -10, число 2 и число -5 являются множителями. Здесь число 2 определяет количество групп, а число -5 определяет количество элементов в каждой группе. Результатом умножения является произведение чисел, в данном случае -10.

Множители могут меняться местами без изменения результата умножения. Например, в выражении 4 * 3 = 12, число 4 и число 3 являются множителями. Здесь число 4 определяет количество групп, а число 3 определяет количество элементов в каждой группе. Результатом умножения является произведение чисел, в данном случае 12.

ПримерПервый множительВторой множительПроизведение

2 * 3	2	3	6
5 * 4	5	4	20
-2 * 3	-2	3	-6

Алгоритм разложения числа на множители

Для разложения числа на множители следует следующие шаги:

1. Выбираем наименьший простой множитель числа. Если число само является простым, то оно является своим единственным множителем.
2. Делим число на этот множитель и записываем его в таблицу.
3. Повторяем первые два шага для полученного частного, пока не получим единицу.
4. Произведение всех множителей из таблицы даст разложение исходного числа на множители.

Давайте рассмотрим пример разложения числа 24 на множители.

МножительЧастное

2	12
2	6
2	3

Для числа 24 разложение на множители будет следующим: 2 * 2 * 2 * 3 = 24.

Алгоритм разложения числа на множители помогает нам лучше понять структуру числа и использовать это знание в различных математических задачах и вычислениях.

Примеры разложения чисел на множители

Например, число 12 можно разложить на множители следующим образом:

12 = 2 × 2 × 3

Таким образом, число 12 разлагается на простые множители 2 и 3. Это означает, что 12 может быть представлено как произведение этих множителей.

Другой пример разложения числа на множители — число 20:

20 = 2 × 2 × 5

Число 20 разлагается на простые множители 2 и 5.

Разложение числа на множители является полезным навыком, который помогает нам лучше понять структуру чисел и проводить различные математические операции.

Разложение числа 12 на множители

В математике разложение числа на множители представляет собой процесс представления данного числа как произведения простых чисел. Разложение числа 12 на множители позволяет нам выразить число 12 как произведение множителей, которые не могут быть разложены на множители дальше.

Число 12 можно разложить на множители следующим образом:

• 12 = 2 × 6
• 12 = 2 × 2 × 3

Как мы видим, число 12 можно представить как произведение простых множителей 2, 2 и 3. Такое разложение называется каноническим разложением на множители.

Разложение числа на множители позволяет нам лучше понять его структуру и свойства. Это важное понятие, которое используется во многих разделах математики, включая алгебру и теорию чисел.

Вопрос-ответ:

Что такое состав числа?

Состав числа — это способ представления числа в виде суммы или разности других чисел. Например, число 8 можно представить в виде суммы 5 и 3, или разности 10 и 2.

Какие основные понятия связаны со составом числа?

Основные понятия, связанные со составом числа, — это слагаемые и разность. Слагаемые это числа, складывая которые, получаем заданное число. Разность это числа, вычитая которые, получаем заданное число.

Какие примеры можно привести для состава числа?

Примеры для состава числа: число 9 можно представить в виде суммы 4 и 5, или разности 12 и 3. Число 7 можно представить в виде суммы 2 и 5, или разности 10 и 3.

Какие навыки развиваются при изучении состава числа?

При изучении состава числа развиваются навыки анализа и синтеза чисел, умение представлять числа в виде суммы или разности других чисел, а также решать простые задачи на сложение и вычитание.

Как можно использовать знания о составе числа в повседневной жизни?

Знания о составе числа могут быть полезными в повседневной жизни, например, при покупках, когда нужно вычислить сумму покупок или сдачу. Также, эти знания помогают в решении различных математических задач и задач на логическое мышление.

Что такое состав числа?

Состав числа — это разложение числа на слагаемые, таким образом, чтобы их сумма равнялась исходному числу.

Как разложить число 8 на слагаемые?

Число 8 можно разложить на слагаемые разными способами. Например, 8 = 4 + 4 или 8 = 3 + 5.

Разложение числа 24 на множители

Чтобы разложить число 24 на множители, мы должны найти все простые числа, на которые 24 делится без остатка.

Для числа 24 простыми множителями являются числа 2 и 3. Мы можем разложить число 24 на множители следующим образом:

24 = 2 × 2 × 2 × 3 = 2³ × 3

Таким образом, число 24 можно разложить на множители 2 и 3 в степенях: 2³ × 3.

Разложение числа на множители является важным понятием в математике и может использоваться, например, для упрощения дробей или нахождения наибольшего общего делителя.

Видео по теме: