Что является статистической оценкой математического ожидания

Статистическая оценка математического ожидания — это числовая характеристика, используемая для описания среднего значения случайной величины на основе выборочных данных. Узнайте, как вычислить и интерпретировать статистическую оценку математического ожидания и ее связь с истинным значением.

Математическое ожидание является одной из основных характеристик случайной величины. Оно представляет собой среднее значение случайной величины, которое можно ожидать при повторении эксперимента большое количество раз. Точное значение математического ожидания не всегда известно, поэтому для его оценки используются статистические методы.

Статистическая оценка математического ожидания основана на выборочных данных, полученных из исследуемой случайной величины. Она позволяет аппроксимировать истинное значение математического ожидания с определенной степенью точности.

Существует несколько методов оценки математического ожидания, включая методы точечной оценки и интервальной оценки. Метод точечной оценки заключается в нахождении единственного числового значения, которое наиболее близко к истинному значению математического ожидания. Метод интервальной оценки позволяет определить диапазон значений, в котором с определенной вероятностью находится истинное значение математического ожидания. Для этого используются доверительные интервалы.

Оценка математического ожидания является важной задачей в статистике и находит применение во многих областях, таких как экономика, финансы, медицина и социология. Правильный выбор метода оценки и адекватная интерпретация результатов позволяют сделать достоверные выводы на основе статистических данных и принять обоснованные решения.

Определение и смысл математического ожидания

Математическое ожидание вычисляется как сумма произведений значений случайной величины на их вероятности. В самом простом случае, когда случайная величина принимает конечное количество значений, формула для вычисления математического ожидания имеет вид:

E(X) = x1p1 + x2p2 + … + xnpn

Где E(X) – математическое ожидание случайной величины X, x1, x2, …, xn – значения случайной величины, p1, p2, …, pn – соответствующие вероятности появления каждого значения.

Математическое ожидание имеет важное практическое применение во многих областях, таких как физика, экономика, финансы, статистика и др. Оно позволяет оценить среднее поведение системы или случайного события и принять обоснованные решения на основе этой информации.

Важность статистической оценки математического ожидания

Статистическая оценка математического ожидания имеет принципиальное значение во многих областях, таких как экономика, физика, медицина, социология и другие. Она позволяет делать выводы о среднем значении и предсказывать поведение случайных величин.

Одним из принципов статистической оценки является использование выборки, представляющей собой часть исследуемой генеральной совокупности. Путем анализа выборки и применения статистических методов можно сделать выводы о математическом ожидании генеральной совокупности.

Статистическая оценка математического ожидания позволяет также проверять гипотезы о равенстве или различии средних значений различных групп или условий. Например, оценка математического ожидания может помочь в исследовании эффективности нового лекарства или в сравнении доходов различных социальных групп.

Важно отметить, что статистическая оценка математического ожидания не является точной, но она позволяет сделать вероятностные выводы о среднем значении и основываться на них при принятии решений.

Поэтому понимание и применение методов статистической оценки математического ожидания является важным для научных исследований, принятия решений и развития различных областей знания.

Методы оценки математического ожидания

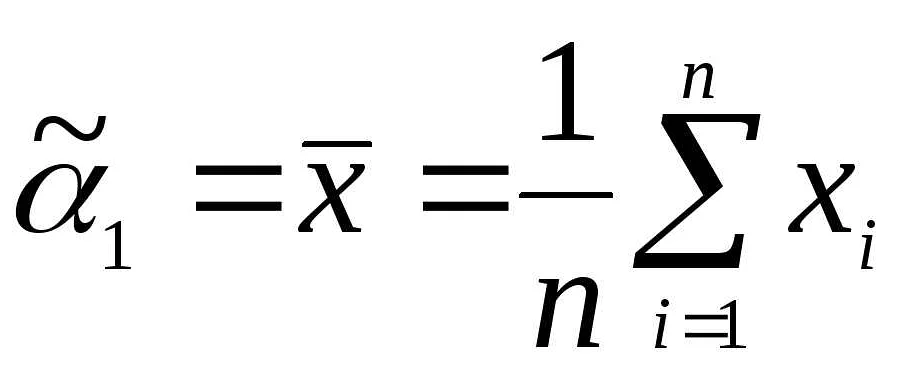
• Выборочное среднее — наиболее простой и распространенный метод оценки математического ожидания. Он основывается на вычислении среднего арифметического значений случайной выборки. Формула для вычисления выборочного среднего выглядит следующим образом:

• Метод моментов — основан на равенстве теоретического момента случайной величины и его оценки на основе выборки. Для применения метода моментов необходимо знать распределение случайной величины и его параметры. Формула для вычисления оценки математического ожидания по методу моментов выглядит следующим образом:

• Метод максимального правдоподобия — основан на выборе такого значения параметра, при котором правдоподобие выборки будет максимальным. Для применения метода максимального правдоподобия необходимо знать функцию плотности распределения случайной величины. Формула для вычисления оценки математического ожидания по методу максимального правдоподобия выглядит следующим образом:

Выбор метода оценки математического ожидания зависит от конкретной задачи и доступных данных. Каждый метод имеет свои преимущества и недостатки, и выбор наиболее подходящего метода требует анализа и сравнения результатов.

Непараметрические методы оценки математического ожидания

Одним из наиболее распространенных непараметрических методов оценки математического ожидания является метод ядерной оценки плотности (Kernel Density Estimation, KDE). Ключевая идея метода заключается в том, чтобы представить выборку данных в виде суммы ядерных функций, центрированных вокруг каждой точки выборки. Затем происходит сглаживание этих ядерных функций и получение оценки плотности вероятности. Математическое ожидание вычисляется как интеграл от оценки плотности.

Другим непараметрическим методом оценки математического ожидания является метод Нельсона-Олсена. Он основан на идеях оценки плотности вероятности и является адаптивным к различным формам данных. Метод Нельсона-Олсена предлагает использовать оконные функции и веса, чтобы получить оценку математического ожидания.

Также существуют другие непараметрические методы оценки математического ожидания, такие как методы наименьших квадратов, ранговые методы, бутстрэп, методы ядерной регрессии и многие другие. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи и доступных данных.

МетодОписание

Метод ядерной оценки плотности	Представление выборки данных в виде суммы ядерных функций и сглаживание
Метод Нельсона-Олсена	Использование оконных функций и весов для получения оценки математического ожидания
Методы наименьших квадратов	Минимизация суммы квадратов отклонений для получения оценки математического ожидания
Ранговые методы	Оценка математического ожидания на основе рангов данных
Бутстрэп	Получение оценки математического ожидания путем генерации случайных выборок
Методы ядерной регрессии	Использование ядерных функций для оценки зависимости между переменными и получения оценки математического ожидания

Параметрические методы оценки математического ожидания

Параметрические методы оценки математического ожидания основаны на предположении о виде распределения исследуемой случайной величины. Эти методы позволяют оценить параметры распределения, в том числе математическое ожидание.

Одним из основных параметрических методов является метод максимального правдоподобия. Суть этого метода заключается в том, чтобы найти такие значения параметров распределения, при которых вероятность получить имеющиеся наблюдения будет максимальной. В результате применения этого метода получается оценка математического ожидания.

Еще одним параметрическим методом оценки математического ожидания является метод моментов. В этом методе основным шагом является приравнивание теоретических моментов распределения к соответствующим выборочным моментам. Из этого равенства можно получить оценку математического ожидания.

Параметрические методы оценки математического ожидания имеют свои преимущества и недостатки. Они требуют предварительного знания о виде распределения исследуемой случайной величины, что может быть затруднительно в некоторых случаях. Однако, при выполнении предположений о распределении, эти методы могут дать более точные оценки математического ожидания, чем непараметрические методы.

Принципы выбора метода оценки математического ожидания

Первым принципом выбора метода оценки математического ожидания является соответствие метода статистической модели. То есть метод оценки должен быть адекватным модели, которая описывает данные. Например, если данные имеют нормальное распределение, то наиболее подходящим методом будет метод максимального правдоподобия.

Вторым принципом является эффективность выбранного метода оценки. Эффективность оценки означает, что оценка должна быть наиболее точной и иметь наименьшую дисперсию среди всех возможных оценок. Для оценки математического ожидания существуют различные методы, такие как метод моментов, метод максимального правдоподобия и методы базирующиеся на бутстрэпе.

Третьим принципом выбора метода оценки является простота и удобство его применения. Часто при работе с данными требуется быстро получить оценку математического ожидания, поэтому метод должен быть достаточно простым и не требовать большого количества вычислений. Например, метод моментов является простым и легко применимым методом оценки.

Четвертым принципом выбора метода является стабильность оценки. Оценка математического ожидания должна быть устойчивой к выбросам и изменениям в данных. Некоторые методы, например, метод максимального правдоподобия, могут быть чувствительны к выбросам и могут давать неправильные оценки в случае их наличия.

И, наконец, пятый принцип — интерпретируемость оценки. Оценка математического ожидания должна быть понятной и иметь смысл с точки зрения исследуемых данных и контекста задачи. Например, если оценка отрицательна, то она может не иметь физического смысла и требует дополнительного анализа и интерпретации.

ПринципОписание

Соответствие метода статистической модели	Метод оценки должен быть адекватным модели, которая описывает данные
Эффективность выбранного метода	Оценка должна быть наиболее точной и иметь наименьшую дисперсию среди всех возможных оценок
Простота и удобство применения	Метод должен быть достаточно простым и не требовать большого количества вычислений
Стабильность оценки	Оценка должна быть устойчивой к выбросам и изменениям в данных
Интерпретируемость оценки	Оценка должна быть понятной и иметь смысл с точки зрения исследуемых данных и контекста задачи

Вопрос-ответ:

Какие методы используются для статистической оценки математического ожидания?

Для статистической оценки математического ожидания используются различные методы, включая методы моментов, метод максимального правдоподобия и методы байесовской оценки.

Что такое математическое ожидание и как его оценивают?

Математическое ожидание — это среднее значение случайной величины или функции случайной величины. Для оценки математического ожидания используются статистические методы, такие как методы моментов, метод максимального правдоподобия и методы байесовской оценки.

Какие принципы лежат в основе статистической оценки математического ожидания?

Основными принципами статистической оценки математического ожидания являются принципы несмещенности, состоятельности и эффективности. Несмещенность означает, что оценка не смещена и имеет тенденцию стремиться к истинному значению параметра. Состоятельность означает, что оценка сходится к истинному значению параметра с ростом объема выборки. Эффективность означает, что оценка имеет наименьшую дисперсию среди всех несмещенных оценок.

Как выбирать метод оценки математического ожидания?

Выбор метода оценки математического ожидания зависит от различных факторов, таких как размер выборки, распределение данных и предположения о параметрах. Методы моментов и метод максимального правдоподобия являются популярными методами, но выбор конкретного метода требует анализа и оценки различных факторов.

Применение статистической оценки математического ожидания в практике

Применение статистической оценки математического ожидания широко распространено в различных областях, таких как экономика, финансы, медицина, социология и другие. Например, в экономике она используется для оценки среднего дохода населения или средней стоимости товаров. В медицине она может применяться для оценки среднего эффекта лекарственного препарата.

Существует несколько методов статистической оценки математического ожидания, включая метод моментов, метод максимального правдоподобия и байесовский подход. Каждый из этих методов имеет свои особенности и предположения, которые должны быть учтены при выборе наиболее подходящего метода для конкретной задачи.

Оценка математического ожидания позволяет получить информацию о среднем значении случайной величины и ее распределении в выборке. Это основа для принятия решений и проведения статистических тестов. Например, на основе оценки математического ожидания можно сравнивать средние значения двух групп и определять статистическую значимость различий.

Важно отметить, что статистическая оценка математического ожидания является приближенной и может содержать ошибку. Поэтому необходимо учитывать доверительный интервал оценки, который показывает диапазон значений, в котором с определенной вероятностью находится истинное значение математического ожидания.

Применение статистической оценки математического ожидания в практике позволяет проводить анализ данных, делать выводы и принимать решения на основе статистических методов. Это является важным инструментом для исследователей, аналитиков и специалистов в различных областях деятельности.

Видео по теме: