Теорема математического анализа о существовании пределов у функции как называется

Теорема математического анализа о существовании пределов у функции — что это за теорема и как она называется? Узнайте в нашей статье, как эта теорема сформулирована и как она применяется в математическом анализе.

Теорема о существовании пределов является одной из фундаментальных теорем математического анализа. Суть этой теоремы заключается в утверждении о существовании предела у функции на некотором отрезке или интервале.

Доказательство этой теоремы основывается на понятии предела функции и определении предела последовательности. Сначала рассматривается случай, когда функция имеет предел на отрезке. Затем доказывается, что если функция имеет предел на интервале, то она имеет предел и на любом отрезке внутри этого интервала.

Для доказательства теоремы о существовании пределов используется метод последовательностей. Сначала выбирается последовательность точек на отрезке (или интервале), стремящаяся к некоторой фиксированной точке. Затем анализируется поведение значений функции на этих точках и показывается, что они также стремятся к некоторому фиксированному числу. Таким образом, доказывается, что функция имеет предел на данном отрезке или интервале.

Теорема о существовании пределов имеет большое значение в математическом анализе, так как позволяет установить существование предела у функции на некотором промежутке. Это понятие является основой для дальнейшего изучения свойств функций и их поведения в различных точках.

Таким образом, теорема о существовании пределов является одной из фундаментальных теорем математического анализа, которая позволяет установить существование предела у функции на отрезке или интервале. Доказательство этой теоремы основывается на понятии предела функции и определении предела последовательности. Она имеет большое значение в математическом анализе и является основой для изучения свойств функций.

Формулировка теоремы

Теорема: Пусть функция f(x) определена на некотором интервале (a, b) и существует конечный предел для x, стремящегося к a или b. Тогда существуют конечные пределы функции f(x) в точках x = a и x = b.

Доказательство: Доказательство данной теоремы основывается на определении предела функции и его свойствах.

Согласно определению предела, для любого положительного числа ε существует положительное число δ, такое что для всех x, удовлетворяющих условию 0 < |x — a| < δ, выполняется неравенство |f(x) — L| < ε, где L — конечный предел функции f(x) при x, стремящемся к a.

Рассмотрим предел функции f(x) при x, стремящемся к a. Пусть L1 — предел функции f(x) при x, стремящемся к a справа, и L2 — предел функции f(x) при x, стремящемся к a слева.

Если L1 = L2 = L, то существует конечный предел функции f(x) в точке x = a.

Если L1 ≠ L2, то существует бесконечность пределов функции f(x) в точке x = a.

Аналогично рассматривается предел функции при x, стремящемся к b.

Таким образом, теорема о существовании пределов у функции утверждает, что если существует конечный предел функции f(x) при x, стремящемся к a или b, то существуют конечные пределы функции f(x) в точках x = a и x = b.

Определение предела функции

Пусть имеется функция f(x), определенная на некотором промежутке около точки a. Говорят, что предел функции f(x) при x стремящемся к a равен L, если для любого положительного числа ε существует положительное число δ такое, что для всех x, удовлетворяющих условию 0 < |x — a| < δ, выполняется неравенство |f(x) — L| < ε.

Это определение можно интерпретировать следующим образом: если значения функции f(x) могут быть сколь угодно близкими к числу L, когда x находится достаточно близко к a, то говорят, что предел функции f(x) при x стремящемся к a равен L.

Определение предела функции позволяет формализовать понятие «приближения» к определенным значениям и является важным инструментом для изучения свойств функций и их поведения в окрестности определенной точки.

Необходимое условие существования предела

Необходимое условие существования предела функции f(x) при x, стремящемся к x0, заключается в том, что существование предела должно быть обеспечено единственным значением для всех последовательностей, сходящихся к x0.

Если для двух последовательностей {x_n} и {y_n}, сходящихся к x0, пределы пределов функции f(x) существуют и равны, то этот предел называется необходимым условием существования предела.

Математически это можно записать следующим образом:

Если существует предел f(x) при x, стремящемся к x0, и для любых последовательностей {x_n} и {y_n}, таких что x_n и y_n сходятся к x0, пределы пределов f(x_n) и f(y_n) существуют и равны, то f(x_n) = f(y_n) при всех n.

Это условие необходимо для того, чтобы у функции существовал предел при данном значении x0. Однако, оно не является достаточным условием, так как существование предела не гарантирует его единственности.

Достаточное условие существования предела

Достаточное условие существования предела заключается в том, что функция должна быть ограничена на некотором интервале, содержащем точку, в которой ищется предел. Если функция ограничена и монотонна на данном интервале, то она обладает пределом в этой точке.

То есть, если существуют такие числа $a$ и $b$, что для всех $x$ из интервала $(a, b)$ выполняется неравенство $m \leq f(x) \leq M$, где $m$ и $M$ — некоторые числа, а функция $f(x)$ монотонно возрастает или монотонно убывает на интервале $(a, b)$, то предел функции $f(x)$ в точке $x_0$ существует и равен $L$, где $L$ — наименьшая верхняя грань множества значений функции на $(a, b)$.

Доказательство существования предела

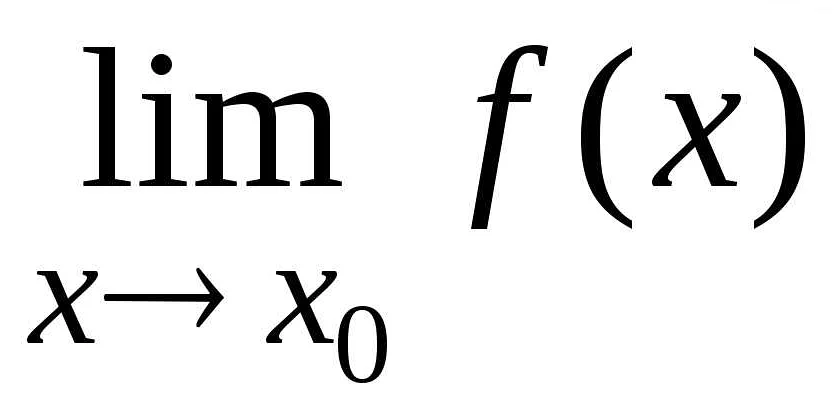
Для доказательства существования предела функции необходимо применить определение предела и последовательно выполнить несколько шагов.

Шаг 1. Пусть дана функция f(x), определенная на некотором интервале (a, b) и точка c является предельной точкой этого интервала. Необходимо доказать, что предел f(x) при x, стремящемся к c, существует.

Шаг 2. Вводим произвольное положительное число ε и ищем такое положительное число δ, что для всех x из интервала (a, b), отличных от c, будет выполняться условие |x — c| < δ. Это необходимо для того, чтобы значения f(x) были близки к значению f(c), когда x находится достаточно близко к c.

Шаг 3. Теперь необходимо найти такое значение M, что для всех x из интервала (a, b), отличных от c и удовлетворяющих условию |x — c| < δ, будет выполняться условие |f(x) — M| < ε. А именно, ищем такое значение M, что функция f(x) остается близкой к M при x, стремящемся к c.

Шаг 4. Доказываем, что найденное значение M является пределом функции f(x) при x, стремящемся к c. Для этого необходимо показать, что для любого положительного числа ε найдется такое положительное число δ, что для всех x из интервала (a, b), отличных от c и удовлетворяющих условию |x — c| < δ, будет выполняться условие |f(x) — M| < ε.

Таким образом, выполнив все эти шаги, мы можем доказать существование предела функции f(x) при x, стремящемся к c.

Видео по теме:

Вопрос-ответ:

Что такое теорема о существовании пределов у функции?

Теорема о существовании пределов у функции утверждает, что если функция ограничена на некотором интервале и имеет монотонное поведение на этом интервале, то у нее существуют конечные пределы на границах этого интервала.

Какую роль играет ограниченность функции в теореме о существовании пределов?

Ограниченность функции на интервале является одним из условий теоремы о существовании пределов. Она гарантирует, что функция не будет стремиться к бесконечности на границах интервала.

Что означает монотонное поведение функции?

Монотонное поведение функции означает, что она либо возрастает на всем интервале, либо убывает на всем интервале. То есть, значение функции увеличивается или уменьшается при увеличении аргумента.

Как доказывается теорема о существовании пределов у функции?

Доказательство теоремы о существовании пределов у функции обычно основано на понятии монотонной последовательности и принципе полноты числовой оси. Оно состоит из нескольких этапов, включающих доказательство ограниченности функции и построение монотонной последовательности, сходящейся к пределу на границе интервала.

Примеры применения теоремы

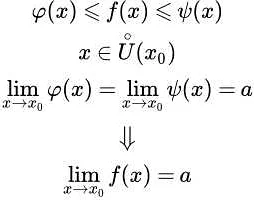
Пример 1: Рассмотрим функцию f(x) = sin(x)/x. Найдем предел этой функции при x стремящемся к нулю. Сначала заметим, что функция определена на всей числовой оси, кроме точки x = 0. Используя теорему о существовании пределов, мы можем записать:

lim(x→0) sin(x)/x = 1,

что означает, что предел функции f(x) = sin(x)/x при x стремящемся к нулю равен 1.

Пример 2: Рассмотрим функцию f(x) = x^2 + 3x + 2. Найдем предел этой функции при x стремящемся к бесконечности. Пользуясь теоремой о существовании пределов, мы можем записать:

lim(x→∞) x^2 + 3x + 2 = ∞,

что означает, что предел функции f(x) = x^2 + 3x + 2 при x стремящемся к бесконечности равен бесконечности.

Пример 3: Рассмотрим функцию f(x) = 1/x. Найдем предел этой функции при x стремящемся к 0. Пользуясь теоремой о существовании пределов, мы можем записать:

lim(x→0) 1/x = ±∞,

что означает, что предел функции f(x) = 1/x при x стремящемся к 0 не существует, но приближается к плюс или минус бесконечности в зависимости от направления приближения.

Полезные свойства пределов функций

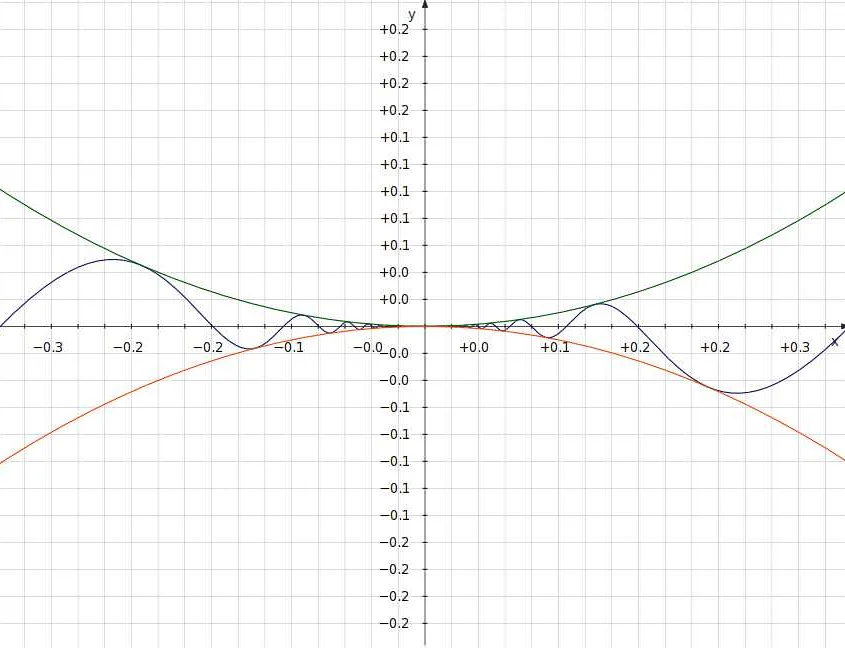
Пределы функций обладают рядом полезных свойств, которые позволяют упростить вычисление пределов и делать выводы о поведении функций.

Сумма пределов: Если функции f(x) и g(x) имеют пределы при x стремящемся к a, то предел их суммы равен сумме пределов:

lim(x→a) (f(x) + g(x)) = lim(x→a) f(x) + lim(x→a) g(x)

Произведение пределов: Если функции f(x) и g(x) имеют пределы при x стремящемся к a, то предел их произведения равен произведению пределов:

lim(x→a) (f(x) * g(x)) = lim(x→a) f(x) * lim(x→a) g(x)

Частное пределов: Если функции f(x) и g(x) имеют пределы при x стремящемся к a, и предел g(x) не равен 0, то предел их частного равен частному пределов:

lim(x→a) (f(x) / g(x)) = lim(x→a) f(x) / lim(x→a) g(x)

Предел композиции функций: Если функции f(x) и g(x) имеют пределы при x стремящемся к a, и g(x) имеет предел при x стремящемся к b, то предел их композиции равен пределу композиции:

lim(x→a) (g(f(x))) = lim(x→a) g(lim(x→a) f(x)) = g(lim(x→a) f(x)) = g(lim(x→b) f(x))

Предел инверсии: Если функция f(x) имеет предел при x стремящемся к a, и предел f(x) не равен 0, то предел ее инверсии равен инверсии предела:

lim(x→a) (1 / f(x)) = 1 / (lim(x→a) f(x))

Эти свойства позволяют упростить вычисление пределов и делать выводы о поведении функций без необходимости применять определение предела и доказывать его существование.