Тригонометрия это раздел математики в котором изучаются

Тригонометрия — это раздел математики, в котором изучаются геометрические и аналитические свойства треугольников и функции, связанные с углами. Она является важной частью математического аппарата и применяется в различных областях, включая физику, инженерию и компьютерные науки.

Тригонометрия – один из основных разделов математики, который изучает связь между углами и сторонами треугольников. Она является неотъемлемой частью геометрии и алгебры, а также находит широкое применение в различных областях науки и техники.

Основные понятия и формулы тригонометрии возникли в Древней Греции и были развиты такими математиками, как Гиппарх, Птолемей и Аристарх. Они создали таблицы значений тригонометрических функций, которые впоследствии стали основой для проведения различных вычислений и построения графиков.

Применение тригонометрии широко распространено в физике, инженерии, астрономии, геодезии, компьютерной графике и многих других областях. С ее помощью можно решать задачи, связанные с измерением расстояний и углов, определением высоты объектов, расчетом сил и напряжений, а также моделированием и анализом сложных систем.

Тригонометрия – это не только набор формул и правил, но и мощный инструмент, который позволяет понять и описать многие явления и закономерности в природе и технике. Ее применение позволяет проводить точные расчеты, строить графики, анализировать данные и прогнозировать результаты экспериментов.

Изучение тригонометрии помогает развить логическое мышление, абстрактное мышление, аналитическое мышление и навыки работы с числами. Оно также развивает способность анализировать информацию, решать проблемы и принимать обоснованные решения. Поэтому знания в области тригонометрии являются необходимыми для успеха в научных и технических профессиях.

Основные понятия тригонометрии

Основные понятия тригонометрии включают следующее:

• Углы: Тригонометрия основана на изучении углов. Углы могут быть измерены в градусах или радианах, и они играют важную роль в определении отношений между сторонами треугольника.
• Стороны: В треугольнике есть три стороны — гипотенуза, противолежащая сторона и прилежащая сторона. Тригонометрические функции помогают найти отношения между этими сторонами.
• Тригонометрические функции: Основными тригонометрическими функциями являются синус, косинус и тангенс. Они определяются как отношения между определенными сторонами треугольника и гипотенузой.
• Тригонометрические тождества: В тригонометрии существует множество тождеств, которые позволяют связать тригонометрические функции между собой и упростить их вычисление.
• Решение треугольников: Тригонометрия позволяет решать различные задачи, связанные с треугольниками, такие как нахождение углов и сторон треугольника, используя известные данные.

Основные понятия тригонометрии являются основой для более сложных концепций и приложений этой науки, таких как геодезия, физика и инженерия.

Тригонометрические функции

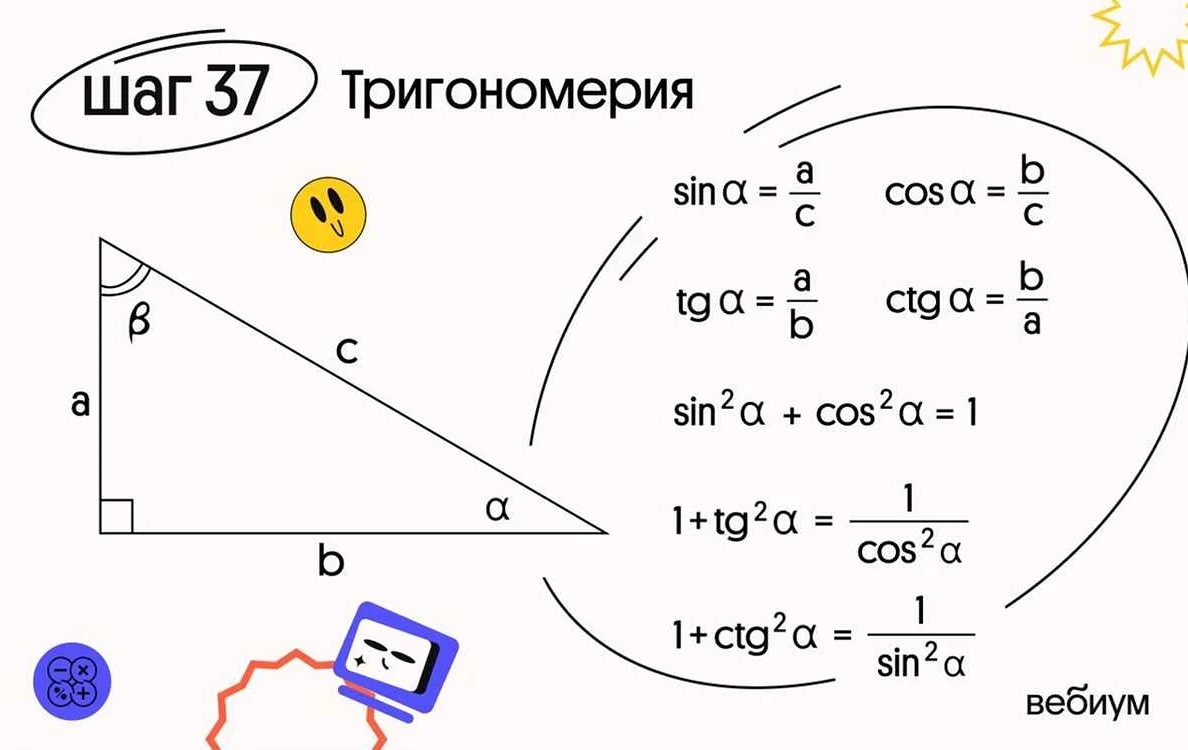
Синус угла определяется как отношение противолежащей катеты к гипотенузе треугольника. Обозначается символом sin.

Косинус угла определяется как отношение прилежащей катеты к гипотенузе треугольника. Обозначается символом cos.

Тангенс угла определяется как отношение противолежащей катеты к прилежащей катете треугольника. Обозначается символом tg или tan.

Тригонометрические функции широко применяются в различных областях науки, инженерии и технике. Они используются для решения задач, связанных с измерением углов, моделированием и анализом колебаний, решением геометрических задач и многими другими.

Тригонометрические тождества

В тригонометрии существуют различные тождества, которые описывают связь между тригонометрическими функциями и углами. Знание этих тождеств позволяет упростить выражения и решать тригонометрические уравнения.

Одно из самых известных тождеств – тождество Пифагора:

Тождество Пифагора:

sin2(x) + cos2(x) = 1

Это тождество отражает соотношение между синусом и косинусом угла, который изменяется в диапазоне от 0 до 90 градусов. Оно является основой для многих других тождеств и формул в тригонометрии.

Другое важное тождество – тождество аддитивности для синуса:

Тождество аддитивности для синуса:

sin(x + y) = sin(x) * cos(y) + cos(x) * sin(y)

Это тождество позволяет выражать синус суммы двух углов через синусы и косинусы исходных углов. Оно находит применение при решении задач на сумму или разность углов.

Также существуют тождества для других тригонометрических функций, таких как косинус, тангенс, котангенс, секанс и косеканс. Знание и использование этих тождеств позволяет упростить выражения и решать различные задачи в тригонометрии.

Тригонометрические преобразования

Основными тригонометрическими функциями являются синус, косинус и тангенс. Тригонометрические преобразования позволяют выразить эти функции через другие тригонометрические функции и обратно.

Тригонометрические преобразования можно использовать для упрощения сложных выражений, нахождения значений тригонометрических функций при различных углах, а также для решения уравнений и неравенств, содержащих тригонометрические функции.

Основными тригонометрическими преобразованиями являются:

• Формулы сложения и вычитания для синуса и косинуса;
• Формулы удвоения и половинного угла для синуса, косинуса и тангенса;
• Формулы приведения для синуса, косинуса и тангенса;
• Формулы суммы и разности для тангенса;
• Формулы секанса, косеканса и котангенса через синус, косинус и тангенс.

Знание тригонометрических преобразований позволяет более гибко и эффективно решать задачи, связанные с треугольниками и углами, и является важным инструментом в различных областях науки и техники.

Применение тригонометрии в геометрии

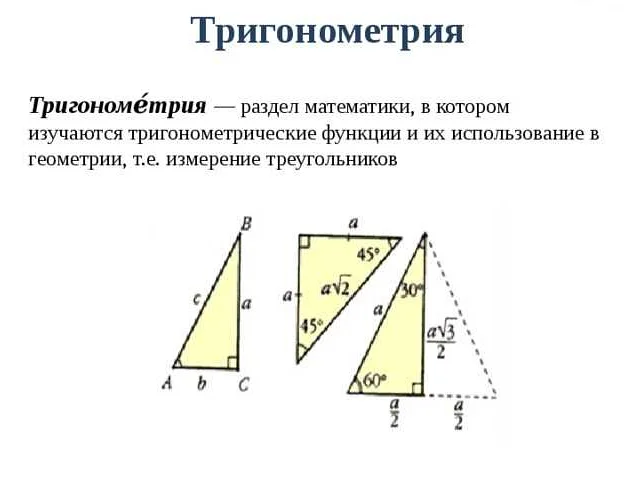
Тригонометрические соотношения позволяют находить значения углов и сторон треугольников, используя известные данные. Для этого применяются функции синуса, косинуса и тангенса. Например, если известны две стороны и один угол треугольника, можно рассчитать все остальные стороны и углы с помощью тригонометрических соотношений.

Теорема синусов является одним из основных инструментов тригонометрии в геометрии. Она позволяет находить соотношение между сторонами и углами треугольника. Теорема утверждает, что отношение длин сторон треугольника к синусам противолежащих углов равно постоянному значению. Это позволяет решать различные задачи, включая нахождение неизвестных сторон и углов треугольника.

Тригонометрия также находит применение в решении задач о высотах и площадях треугольников. Например, с помощью тригонометрии можно найти высоту треугольника, проведенную из одного из вершин, если известны стороны треугольника и углы. Также тригонометрические соотношения позволяют находить площади треугольников, используя известные стороны и углы.

В геометрии тригонометрия находит применение в различных областях, включая расчеты в треугольной геометрии, нахождение площадей многоугольников, построение графиков функций и решение геометрических задач. Понимание и применение тригонометрии в геометрии позволяет решать сложные задачи, связанные с углами и сторонами треугольников, и расширяет возможности геометрических исследований.

Вопрос-ответ:

Зачем изучать тригонометрию?

Изучение тригонометрии позволяет понять связь между углами и сторонами треугольников, а также применять ее в решении различных задач и задачей в различных областях науки и техники. Тригонометрия является основой для изучения геометрии и алгебры, а также широко применяется в физике, инженерии, астрономии и других науках.

Какие основные функции в тригонометрии?

Основные тригонометрические функции: синус, косинус и тангенс. Синус угла определяется как отношение противолежащего катета к гипотенузе треугольника, косинус — как отношение прилежащего катета к гипотенузе, а тангенс — как отношение синуса косинуса.

Как определить значения тригонометрических функций?

Значения тригонометрических функций можно определить с помощью таблиц, графиков или с помощью калькулятора, который имеет функции синуса, косинуса и тангенса. Значения функций зависят от величины угла, выраженного в радианах или градусах.

Как считается синус и косинус отрицательного угла?

Синус и косинус отрицательного угла равны соответственно синусу и косинусу положительного угла с такой же величиной. Таким образом, синус отрицательного угла равен синусу его дополнения, а косинус отрицательного угла равен косинусу его дополнения.

Какие свойства имеют тригонометрические функции?

Тригонометрические функции обладают рядом свойств, включая периодичность, симметрию и ограниченность. Синус и косинус являются периодическими функциями с периодом 2π (или 360 градусов), тангенс не имеет периода. Синус и косинус являются четными функциями, т.е. f(-x) = f(x), а тангенс является нечетной функцией, т.е. f(-x) = -f(x). Также синус и косинус ограничены значениями от -1 до 1, а тангенс не имеет ограничений.

Что такое тригонометрия?

Тригонометрия — это раздел математики, который изучает связи между углами и сторонами треугольников.

Применение тригонометрии в физике

Одно из основных применений тригонометрии в физике – измерение расстояний и высот. С помощью треугольников и тригонометрических функций можно определить расстояние до недоступных объектов, таких как звезды, или высоту недоступных сооружений, например, высоту горы.

Тригонометрия также широко используется при изучении движения тел. С помощью тригонометрических функций можно описать траекторию движения, вычислить скорость и ускорение объекта.

Еще одно важное применение тригонометрии в физике связано с изучением колебаний и волн. Тригонометрические функции позволяют описать характеристики колебательных процессов, такие как амплитуда, частота и фаза.

Также тригонометрия применяется при изучении электрических цепей и схем. Она позволяет определить фазовые углы, вычислить сопротивление и емкость элементов цепи.

Применение тригонометрии в физике – неотъемлемая часть изучения этой науки. Она позволяет упростить и точнее описать различные физические явления и является незаменимым инструментом для решения задач и проведения экспериментов.

Применение тригонометрии в физике:

Измерение расстояний и высот

Изучение движения тел

Изучение колебаний и волн

Изучение электрических цепей и схем

Видео по теме: