Варианта выборки в математике: определение, типы и примеры

В статье рассказывается о понятии варианты выборки в математике и их применении. Вы узнаете, что такое комбинаторика и как с помощью формул можно вычислить количество вариантов выборки из множества объектов. Кроме того, статья описывает различные типы выборок и их свойства, что поможет вам лучше понять эту тему.

Наверняка каждый из нас сталкивался с выборкой предметов в повседневной жизни — будь то выбор товаров в магазине или выбор любимого блюда в меню ресторана. Но что такое выборка в математике? Отличается ли она от выборки в повседневной жизни? В данной статье мы рассмотрим виды выборок в математике, приведем примеры и разберем правила их составления.

Выборка — это один из основных элементов статистики. В математике выборкой называют процесс выбора случайных элементов из группы объектов (например, людей, товаров или чисел). Эти элементы обычно выбираются для определения характеристик всей группы. Например, мы можем выбрать случайные людей из определенной группы и изучать их вес или рост, чтобы сделать выводы о среднем весе или росте всех людей в этой группе.

В данной статье мы рассмотрим три основных вида выборок в математике: простую, систематическую и стратифицированную. Каждая из этих выборок имеет свои особенности и способы составления. Мы также рассмотрим примеры каждой выборки и разберем, как эти примеры могут помочь нам лучше понять концепцию выборок в математике.

Случайная выборка: определение и особенности

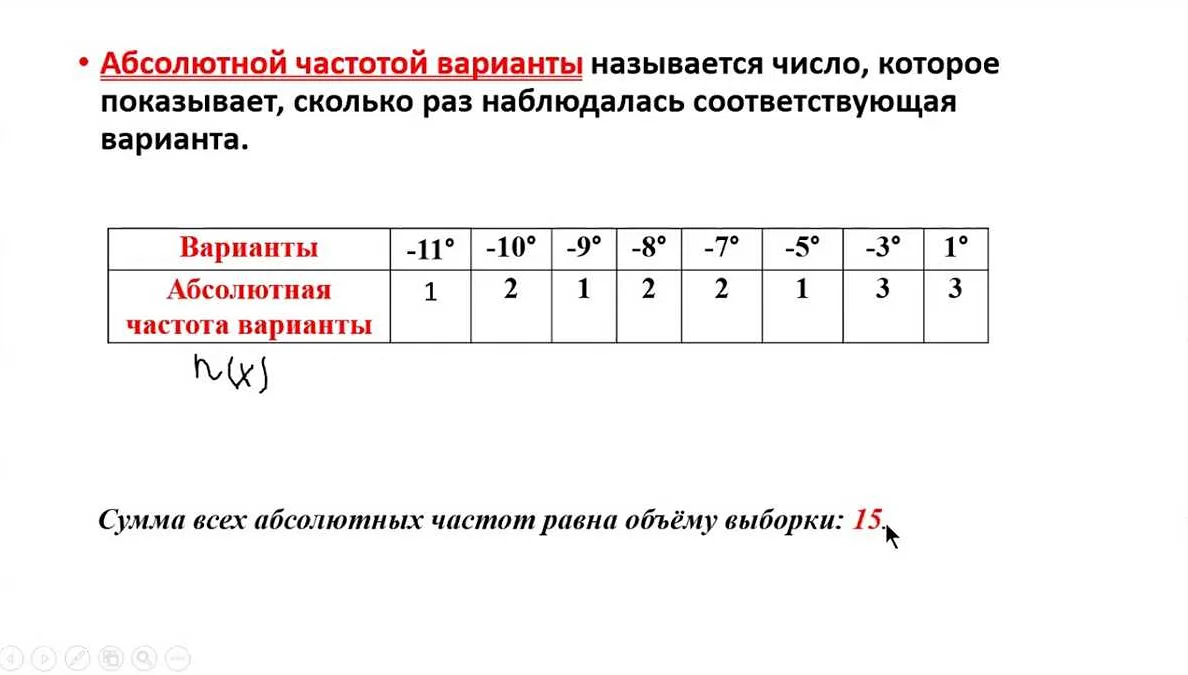
Случайная выборка — это один из видов выборки в математической статистике. Она представляет собой выборку, в которой каждый элемент имеет одинаковую вероятность быть выбранным.

Суть случайной выборки заключается в том, что каждый элемент может быть выбран независимо от других элементов в выборке, и все элементы имеют одинаковый шанс быть выбранными. Следовательно, каждый элемент выборки не зависит от других элементов и не предопределен заранее.

Основным преимуществом случайной выборки является то, что она позволяет получить репрезентативную выборку с минимальной вероятностью искажения данных. Также случайная выборка удобна в использовании для статистических расчетов и прогнозирования.

Для составления случайной выборки необходимо определить количество элементов, которые нужно выбрать и затем выбирать элементы в случайном порядке. Это может быть сделано с помощью различных методов, таких как генерация случайных чисел или использование таблицы случайных чисел.

Вывод: Важно понимать, что случайная выборка является одним из видов выборки в математической статистике, заключающейся в выборе элементов с равной вероятностью. Она позволяет получить репрезентативную выборку с минимальной вероятностью искажения данных и удобна в использовании для статистических расчетов и прогнозирования. Для составления случайной выборки необходимо определить количество элементов, которые нужно выбрать, и выбирать элементы в случайном порядке с помощью различных методов.

Простая случайная выборка: примеры и правила составления

Простая случайная выборка является наиболее распространенным видом выборки в математике и статистике. В этом случае каждый элемент в генеральной совокупности имеет равные шансы быть выбранным в выборку. Таким образом, простая случайная выборка позволяет получить наиболее надежные и объективные результаты.

Примеры простой случайной выборки можно найти во многих областях, включая медицину, социологию, экономику и т.д. Например, если исследование проводится среди населения определенного города, то все жители должны иметь равные шансы попасть в выборку.

Составление простой случайной выборки требует следования нескольким правилам. Во-первых, необходимо определить генеральную совокупность, т.е. все элементы, которые могут быть включены в выборку. Затем, каждый элемент должен быть пронумерован и случайным образом выбран с помощью генератора случайных чисел.

Для получения более точных результатов, требуется максимально увеличить размер выборки. Чем больше элементов будет включено в выборку, тем больше будет точность и надежность полученных результатов. Однако, необходимо учитывать ограничения на количество элементов, которые могут быть включены в выборку в зависимости от доступных ресурсов и времени.

В целом, простая случайная выборка является наиболее простым и в то же время эффективным способом выборки в математике и статистике. Ее правила и примеры могут быть применены во многих областях и помогают получить объективные результаты и выводы.

Систематическая выборка: принцип и свойства

Систематическая выборка — это метод выборки элементов из генеральной совокупности с использованием определенного шага. В этом методе выбирается первый элемент случайным образом, а затем выборка осуществляется с определенным интервалом между элементами.

Принцип систематической выборки заключается в том, что каждый элемент должен иметь равные шансы попасть в выборку. Для обеспечения этого, размер выборки должен быть достаточно большим, чтобы гарантировать, что каждый элемент генеральной совокупности будет иметь равные шансы быть выбранным.

Систематическая выборка имеет несколько свойств, которые делают ее полезной в некоторых ситуациях. Во-первых, этот метод можно использовать, если порядок элементов имеет значение. Во-вторых, он позволяет значительно снизить затраты на выборку, поскольку не требуется выбирать каждый элемент случайным образом. В-третьих, систематическая выборка позволяет уменьшить вероятность ошибки выборки по сравнению с простой случайной выборкой, поскольку элементы выбираются в определенном порядке.

Кластерная выборка: определение и использование

Кластерная выборка – это один из способов случайной выборки, который основан на разделении данных на группы, или кластеры, по определенным признакам. При этом элементы внутри кластера должны быть как можно более схожими между собой, а различия между кластерами – как можно более заметными.

Для создания кластеров используются различные методы, такие как иерархический анализ, метод k-средних и другие. После того, как кластеры сформированы, из каждого кластера можно выбрать случайные элементы. Таким образом, кластерная выборка позволяет уменьшить вариативность данных и выделить группы, наиболее подходящие для исследования.

Кластерная выборка широко применяется в различных областях, например, в медицине для исследования групп риска, в экономике для анализа рынков и потребительских предпочтений, в социологии для исследования национальных и культурных особенностей и т.д.

Однако, следует помнить, что используя кластерную выборку, необходимо иметь четкое понимание того, как формировать кластеры и какие признаки использовать для этого. Неправильный выбор признаков или их некорректная интерпретация может привести к искажению результатов исследования.

Таким образом, кластерная выборка – это один из инструментов, позволяющих выбрать представительную выборку на основе характеристик данных. Однако, перед использованием этого метода, необходимо понимание, как правильно сформировать кластеры и какие признаки использовать для этого.

Стратифицированная выборка: основные принципы и правила

Стратифицированная выборка является одним из видов выборки в математике. Она заключается в разделении выборки на несколько групп (страт) с последующим отбором случайных элементов из каждой группы.

При выборе стратифицированной выборки необходимо учитывать, что разделение выборки на группы должно быть основано на существенных признаках, которые могут повлиять на исследуемый показатель. Также важно определить размер каждой страты, чтобы избежать перекоса в выборке.

Для составления стратифицированной выборки можно использовать различные методы, такие как пропорциональное распределение, равномерное распределение и оптимальное распределение. При этом нужно помнить, что каждый метод имеет свои преимущества и недостатки, и выбор конкретного метода зависит от цели исследования.

Одним из главных преимуществ стратифицированной выборки является повышение точности и надежности результатов исследования. Это обусловлено тем, что каждая страта представляет собой более однородную группу элементов, чем вся выборка в целом.

Важно учесть, что при использовании стратифицированной выборки требуется большее количество времени и ресурсов на ее составление и обработку результатов. Однако, если проведено правильно, то результаты будут более точными и надежными, чем при использовании других видов выборки.

Удобственная выборка: понятие и особенности

Удобственная выборка — это метод выборки элементов из генеральной совокупности, при котором выборка производится на основании доступности или удобства доступа к данным элементам. В этом случае выбираются те элементы генеральной совокупности, которые уже являются расположенными вблизи исследователя или доступны ему для изучения без особых препятствий.

Основной преимуществом удобственной выборки является относительная простота и скорость процесса сбора данных, поскольку исследователю не требуется тратить необходимое время и средства на организацию процесса выборки. Более того, данный метод выборки позволяет получать новые знания и информацию об объектах генеральной совокупности, от которых было бы трудно получить данные с помощью других методов выборки.

Однако, удобственная выборка также обладает некоторыми недостатками. В частности, выборка может быть смещенной, поскольку данные элементы генеральной совокупности, которые доступны для выборки, могут не являться представительными для всей генеральной совокупности и не отражать ее характеристик в полной мере. Кроме того, из-за того, что исследователю не требуется осуществлять специализированные мероприятия по выборке, риски ошибок исследования связанных с выборкой могут быть значительными.

Таким образом, удобственная выборка может быть эффективным методом в определенных условиях, однако, перед выбором данного метода, необходимо тщательно рассмотреть все его плюсы и минусы, а также взвесить все возможные риски исследования, связанные с выборкой.

Пошаговое руководство по выбору наиболее подходящего типа выборки

Шаг 1: Определите цель исследования. Необходимо понимать, какой ответ вы хотите получить, и на какой выборке лучше этот ответ получить. Если вы хотите узнать, как много людей ежедневно посещают определенный магазин, то выбирайте простую случайную выборку.

Шаг 2: Оцените размер исследования. Если исследование очень маленькое, у вас может не быть достаточно данных, чтобы сделать уверенные выводы. В таком случае, выбирайте стратифицированную или кластерную выборку.

Шаг 3: Рассмотрите доступность и доступность ресурсов. Если вы не имеете доступа ко всей группе людей, то вам нужно использовать вероятностные способы выборки, такие как кластерная или стратифицированная выборка.

Шаг 4: Убедитесь, что выборка представляет всю популяцию. Если вы выбираете выборку, то необходимо убедиться, что выбранный тип выборки представляет всю популяцию. Если это не так, и ответы могут быть не точными. Например, если вы выбираете случайную выборку, чтобы понять, как студенты учатся по всей стране, выборка должна быть сбалансированной.

Шаг 5: Подумайте о статистических тестах. Классические статистические тесты используются для проверки гипотез о различиях между выборками. При выборе типа выборки учитывайте, нужно ли вам использовать эти тесты, и выбирайте тип выборки в соответствии с этим.

Шаг 6: Определите методы сбора данных. Соответствующий метод сбора данных помогает убедиться, что выборка точна и представляет всю популяцию. Например, если вы выбираете случайную выборку, то хороший метод — опрос или анкетирование.

Выбор определенного типа выборки зависит от ряда факторов, и надо учитывать множество факторов, а не только два или три. Поэтому необходимо просматривать все факторы вместе, используя описанные шаги. И только после этого можно решить, какой тип выборки наиболее подходит для получения нужной информации.

Влияние выборки на результаты исследований: анализ ошибок

Один из наиболее важных нюансов в работе с выборками – это то, как они могут повлиять на результаты исследований. Проблема заключается в том, что выборки не всегда являются идеальными отражениями всех элементов генеральной совокупности. Поэтому необходимо выяснить, какие ошибки могут возникнуть в работе с выборками и как их можно избежать.

Во-первых, возможна ошибка выборки. Эта ошибка происходит в случае, когда выбранные элементы не возможно однозначно отражают данные генеральной совокупности. Эту ошибку можно частично избежать, если выбирать элементы случайным образом и убедиться в достаточной их репрезентативности.

Во-вторых, возможна ошибка смещения. Она происходит, когда выбранная выборка не является репрезентативной по отношению к генеральной совокупности. В этом случае результаты исследования будут смещенными в одну или другую сторону и не отражают реального положения дел.

Также необходимо учитывать, что размер выборки также может влиять на результаты исследования. Эффекты могут быть как положительными, так и отрицательными. С одной стороны, большие выборки, как правило, дают более точные результаты, но с другой стороны, при использовании больших выборок требуется больший объем вычислений, что делает исследования более сложными.

Важно также учитывать, что выборки должны быть составлены таким образом, чтобы исследование не страдало от ошибок группировки и выбора параметров. Эти ошибки могут быть связаны с тем, какие элементы были выбраны для анализа и каким образом они были сгруппированы. Их избежать можно путем использования правильных методов выборки, группировки и оценки параметров в исследовании.

В результате, работа с выборками – это сложный и ответственный процесс, требующий соответствующих знаний и навыков. Грамотная работа с выборками позволит достигать более точных и объективных результатов исследования и ускорит процесс изучения важных проблем в наших областях знания.

Сравнение различных типов выборки на примере конкретных исследований

Выборка — это процесс отбора определенного количества элементов из группы, с целью их исследования. Чтобы получить максимально точные данные при исследовании популяции, необходимо разобраться в различных типах выборок и правильно выбрать подходящий.

Рассмотрим пример сравнения двух типов выборки на определенном исследовании. На основе данных о среднеквадратическом отклонении полученных результатов оценки уровня образования в двух разных группах по группе людей, мы можем сделать вывод о том, что подходящей будет систематическая выборка, а не произвольная. Систематическая выборка уменьшает смещение оценок и позволяет получать более точные результаты.

На другом примере исследования экспертов определяли, какие бренды украшений являются наиболее популярными среди женщин разных возрастных групп. С использованием железнодорожной выборки было выяснено, что самые популярные бренды не являются одинаковыми для всех возрастных групп. Таким образом, было сделано заключение, что использование железнодорожной выборки позволяет получить более точную информацию о популярности брендов среди определенных возрастных групп.

Таким образом, выбор правильного типа выборки может оказать влияние на точность полученных данных. Каждый тип выборки хорош для определенных задач, поэтому важно знать, какие результаты мы хотим получить и какой подход лучше применить в каждом конкретном случае.

Видео по теме:

Вопрос-ответ:

В чем заключается смысл выборки в математике?

Выборка в математике используется для анализа статистических данных путем отбора части значений из генеральной совокупности и их последующего исследования.

Какие виды выборки существуют?

Существуют несколько видов выборки в математике: случайная, систематическая, стратифицированная, кластерная.

Что такое случайная выборка?

Случайная выборка — это выборка, получаемая случайным образом путем случайного отбора значений из генеральной совокупности.

Как проводится систематическая выборка?

Систематическая выборка — это выборка, полученная путем выбора каждого k-го элемента из генеральной совокупности. Значение k определяется путем деления размера генеральной совокупности на размер выборки.

Что такое стратифицированная выборка и как она составляется?

Стратифицированная выборка — это выборка, получаемая путем разбиения генеральной совокупности на несколько страт и отбора случайных значений из каждой страты в соответствии с их весом в общей генеральной совокупности.

Как составляется кластерная выборка?

Кластерная выборка — это выборка, получаемая путем разбиения генеральной совокупности на кластеры (группы) и отбора случайных кластеров, включающих все элементы, для анализа.

Как выбрать подходящий вид выборки для своей задачи?

Выбор видов выборки зависит от целей исследования, особенностей генеральной совокупности, объема выборки и статистических инструментов, используемых для анализа данных.

Примеры применения выборки в математических задачах и исследованиях

Выборка — это группа элементов некоторого множества, выбранных определенным способом для последующего исследования. Выборка в математике используется в различных задачах и исследованиях. Ниже описаны несколько примеров применения выборки в математических задачах и исследованиях.

• • Определение среднего значения выборки

Одно из наиболее распространенных использований выборки в математике — определение среднего значения выборки. Выборка может представлять собой группу чисел, и на основе этой выборки можно рассчитать среднее значение, что поможет оценить общие тенденции в данных и принять правильные решения, например, в бизнесе.

• • Определение вероятности события

Выборка также может использоваться для определения вероятности определенного события. Например, на основе выборки можно определить вероятность того, что покупатель купит определенный товар в магазине.

• • Определение корреляции между двумя величинами

Выборка может быть использована для определения корреляции между двумя величинами. На основе выборки можно рассчитать коэффициент корреляции, который покажет, насколько сильно две величины связаны друг с другом. Например, можно использовать выборку для определения корреляции между доходом и уровнем образования.

• • Исследование генеральной совокупности через выборку

Выборка может быть использована для исследования генеральной совокупности. Например, исследование выборки может помочь выяснить, как изменится популяция города в ближайшие годы.

• • Определение доверительного интервала

Выборка может использоваться для определения доверительного интервала, который показывает, какой диапазон значений является оптимальным для конкретной характеристики. Например, на основе выборки можно определить доверительный интервал для ожидаемой выручки компании в следующем квартале.

Выводы и рекомендации

Исходя из рассмотренных видов выборок, можно сделать следующие выводы:

1. Простая случайная выборка – наиболее объективный и надежный метод выборки, однако может потребовать значительных материальных и временных затрат.
2. Стратифицированная выборка – удобный метод, позволяющий выделить подгруппы и исследовать их более детально, однако требует дополнительной работы по выделению страт и их размерам.
3. Кластерная выборка – метод, позволяющий сократить затраты на выборку при интересующем большом объеме исходной совокупности, однако может привести к искажению результатов из-за возможного локализованного характера выборки.
4. Систематическая выборка – простой и удобный метод, однако может привести к искажению результатов из-за возможной регулярности в размещении элементов выборки.

Для правильного выбора метода необходимо учитывать конкретные условия исследования, доступные ресурсы и возможные ограничения.

Рекомендации по правилам составления выборки:

• Определить цель исследования;
• Выбрать метод выборки, учитывая условия исследования;
• Определить размер выборки и исходную совокупность;
• Составить список элементов выборки;
• Случайным образом выбрать элементы из списка с помощью генератора случайных чисел или программы выборки;
• Проверить правильность и репрезентативность выборки.

Соблюдение правил составления выборки позволит получить объективные и достоверные результаты исследования и уменьшить вероятность искажения, связанного с выбором неадекватного метода выборки или неправильной комбинацией методов при большом объеме исходной совокупности.