Что такое величины в математике 2

Величины в математике 2 — это концепция, которая описывает свойства и атрибуты объектов, которые измеряются или сравниваются в математике. Величины могут быть числовыми или нечисловыми, а их особенности зависят от контекста, в котором они используются. Величины играют важную роль в различных разделах математики, таких как алгебра, геометрия и статистика.

Величины являются одним из основных понятий в математике. Они используются для измерения, описания и сравнения различных объектов и явлений. Величины могут быть представлены числами, буквами или символами и могут иметь различные значения и единицы измерения.

В математике различают два основных типа величин: дискретные и непрерывные. Дискретные величины могут принимать только определенные значения, например, количество детей в семье или количество машин на парковке. Непрерывные величины могут принимать любые значения в определенном диапазоне, например, время или длина.

Кроме того, величины могут быть абсолютными и относительными. Абсолютные величины имеют конкретные значения и не зависят от других факторов, например, масса или объем. Относительные величины зависят от других факторов и выражаются в виде отношения, например, проценты или коэффициенты.

Величины играют важную роль в различных областях науки и техники. Они помогают установить закономерности, провести анализ данных и принять обоснованные решения. Понимание основных типов и характеристик величин является важным шагом для развития математического мышления и применения математических методов в реальной жизни.

Определение понятия «величина»

Величина может быть числовой или нумерационной. Числовая величина представляет собой количественное измерение, которое может быть выражено числом. Например, длина, масса, время, скорость — все эти величины можно измерить числами. Нумерационная величина, с другой стороны, используется для классификации и нумерации объектов или явлений. Например, номер автобуса, название книги, код товара — все это нумерационные величины.

Каждая величина имеет единицы измерения, которые определяются и используются для сопоставления с другими величинами того же типа. Единицы измерения позволяют проводить сравнение и математические операции с величинами, а также устанавливают стандарты и международные системы измерений.

Величины в математике могут быть как дискретными, так и непрерывными. Дискретная величина может принимать только определенные значения, которые можно перечислить. Например, количество студентов в классе или число попыток, сделанных на экзамене. Непрерывная величина, с другой стороны, может принимать любое значение в определенном диапазоне. Например, рост человека или время, затраченное на выполнение задания.

Тип величиныПримеры

Числовая	Длина, масса, время, скорость
Нумерационная	Номер автобуса, название книги, код товара
Дискретная	Количество студентов, число попыток
Непрерывная	Рост человека, время выполнения задания

Основные классификации величин

Величины в математике могут быть классифицированы по различным критериям. Некоторые из основных классификаций величин включают:

1. По характеру измерения:

а) Скалярные величины — это те, для которых достаточно указать только их числовое значение. Примеры таких величин включают время, массу и температуру.

б) Векторные величины — это те, для которых необходимо указать не только числовое значение, но и направление и точку приложения. Примеры таких величин включают силу, скорость и ускорение.

2. По способу измерения:

а) Абсолютные величины — это те, которые могут быть измерены независимо от других величин. Примеры таких величин включают длину, массу и время.

б) Относительные величины — это те, которые измеряются относительно других величин. Примером такой величины может быть коэффициент увеличения или уменьшения.

3. По изменчивости:

а) Постоянные величины — это те, которые остаются неизменными в течение всего рассматриваемого времени или пространства. Примером такой величины может быть число Пи (π).

б) Изменчивые величины — это те, которые могут меняться в зависимости от времени или условий. Примером такой величины может быть скорость движения тела.

4. По статичности:

а) Дискретные величины — это те, которые могут принимать только конечное или счетное множество значений. Примером такой величины может быть количество студентов в классе.

б) Непрерывные величины — это те, которые могут принимать любое значение в определенном диапазоне. Примером такой величины может быть время или длина.

Эти классификации помогают упорядочить и классифицировать различные величины, что важно для их изучения и применения в математике и других областях науки и техники.

Абсолютные и относительные величины

Абсолютные величины представляют собой значения, которые не зависят от других факторов или отношений. Эти величины имеют определенные единицы измерения и могут быть измерены конкретными числами. Например, длина, вес, время — все это примеры абсолютных величин. Например, если мы говорим о длине стола, то это конкретное измерение, которое мы можем выразить в сантиметрах или метрах.

Относительные величины, в отличие от абсолютных, представляют собой значения, которые зависят от других факторов или отношений. Они не имеют конкретных единиц измерения и обычно выражаются в процентах или долях. Например, если мы говорим о приросте населения, то это не конкретное значение, а изменение в процентах или долях относительно начального значения. Это позволяет нам сравнивать различные объекты или явления и оценивать их взаимосвязь и влияние друг на друга.

Важно понимать разницу между абсолютными и относительными величинами, так как они имеют разные применения и используются в различных областях математики и науки. Понимание этих понятий поможет нам более точно и качественно описывать и анализировать различные явления и процессы.

Абсолютные величиныОтносительные величины

Длина	Процентное изменение
Вес	Доля от общего количества
Время	Коэффициент корреляции

Основные единицы измерения величин

Величины в математике измеряются с помощью различных единиц измерения. Они позволяют нам описывать и сравнивать разные физические и абстрактные объекты.

Существует несколько основных единиц измерения, которые используются в различных областях:

• Масса измеряется в килограммах (кг).
• Длина измеряется в метрах (м).
• Время измеряется в секундах (с).
• Температура измеряется в градусах Цельсия (°C) или в Кельвинах (K).
• Объем измеряется в кубических метрах (м³) или литрах (л).
• Сила измеряется в ньютонах (Н).
• Энергия измеряется в джоулях (Дж).
• Мощность измеряется в ваттах (Вт).

Каждая из этих единиц имеет свои собственные символы и формулы для вычислений. Знание основных единиц измерения позволяет нам проводить точные и однозначные измерения и расчеты в математике и науке в целом.

Использование правильных единиц измерения является важным аспектом точности и надежности научных и инженерных исследований.

Размерность величин

Размерность величины может быть задана с помощью различных методов. Один из самых распространенных методов – использование системы единиц измерения, такой как СИ (Система Международных Единиц). В рамках СИ каждая величина имеет свою базовую единицу измерения, которая определяет ее размерность.

Например, для измерения длины используется базовая единица метр (м). Для измерения массы – килограмм (кг), а для измерения времени – секунда (с). Если величина имеет размерность, отличную от базовой, то для ее измерения могут использоваться префиксы, которые изменяют значение единицы измерения.

Размерность величин может быть как простой, так и сложной. Простая размерность означает, что величина измеряется только в одной единице. Например, длина измеряется только в метрах. Сложная размерность означает, что величина измеряется в нескольких единицах, например, скорость измеряется в метрах в секунду.

Правильное определение размерности величин является важным аспектом в математике, так как позволяет проводить корректные вычисления и анализировать результаты. Кроме того, понимание размерности величин помогает в решении различных задач и применении математики в реальной жизни.

Вопрос-ответ:

Какие бывают величины в математике?

В математике существуют различные виды величин, такие как скаляры, векторы и матрицы. Скаляр — это просто число, вектор — это набор чисел с определенным направлением и длиной, а матрица — это прямоугольная таблица чисел.

Что такое скаляр?

Скаляр — это просто число в математике. Он не имеет никаких направлений или осей, он просто представляет собой единичное значение. Примерами скаляров являются такие величины, как время, масса или температура.

Что такое вектор?

Вектор — это набор чисел, который имеет определенное направление и длину. В математике векторы обычно представляются в виде стрелок на графике или в виде списка чисел. Они широко используются для представления физических величин, таких как скорость и сила.

Какие свойства имеют векторы?

Векторы обладают рядом свойств, таких как сложение и умножение на скаляр. Сложение векторов выполняется покомпонентно, то есть каждый элемент вектора складывается с соответствующим элементом другого вектора. Умножение вектора на скаляр также выполняется покомпонентно, каждый элемент вектора умножается на скалярное значение.

Что такое матрица?

Матрица — это прямоугольная таблица чисел. Она состоит из строк и столбцов, и каждый элемент матрицы имеет свое значение. Матрицы используются в математике для решения систем линейных уравнений и для представления линейных преобразований.

Какие бывают величины в математике?

В математике существуют различные типы величин. Они могут быть дискретными или непрерывными, а также могут быть качественными или количественными. Количественные величины могут быть дискретными или непрерывными, в зависимости от того, могут ли они принимать только определенные значения или любые значения в определенном диапазоне. Качественные величины, с другой стороны, не могут быть измерены числовыми значениями и могут быть только категоризированы.

Что такое дискретные величины?

Дискретные величины — это величины, которые могут принимать только определенные значения. Например, количество студентов в классе или количество братьев и сестер у каждого человека. Дискретные величины обычно являются целыми числами и могут быть перечислены по порядку. Они также могут быть представлены в виде таблицы или графика.

Перевод величин из одних единиц в другие

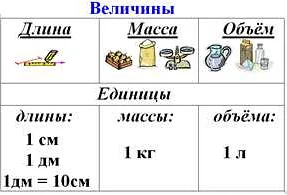
Величины в математике могут быть выражены в различных единицах измерения. Часто возникает необходимость перевести величины из одних единиц в другие, чтобы получить более удобные или привычные значения.

Для перевода величин из одних единиц в другие необходимо знать соответствующие коэффициенты перевода. Величина, измеренная в исходной единице, умножается на коэффициент перевода, чтобы получить значение в новых единицах.

Например, при переводе длины из метров в километры необходимо знать, что 1 километр равен 1000 метров. Таким образом, чтобы перевести 500 метров в километры, нужно разделить значение в метрах на коэффициент перевода: 500 метров / 1000 = 0.5 километра.

Также для перевода величин могут использоваться префиксы, которые обозначают десятичные кратности единицы измерения. Например, префикс «кило-» означает умножение на 1000, префикс «милли-» — деление на 1000. Таким образом, килограмм можно перевести в граммы, умножив значение в килограммах на 1000, а метры в миллиметры — умножив на 1000.

При переводе величин из одних единиц в другие необходимо быть внимательным, чтобы правильно использовать коэффициент перевода и префиксы, чтобы получить корректное значение в новых единицах.

Перевод величин из одних единиц в другие является важным навыком в математике и может быть полезным в различных областях науки, техники и повседневной жизни.

Видео по теме: