Что такое верное неравенство в математике 5 класс

Верное неравенство в математике 5 класс — это неравенство, которое выполняется для всех значений переменных в данном контексте. Узнайте, как определить и решить верное неравенство в 5 классе математики.

Неравенство — одно из основных математических понятий, которое изучается уже в начальной школе. В 5 классе ученики углубляют свои знания о неравенствах и учатся работать с ними. Неравенства могут сравнивать числа, выражения или переменные. Важно понимать, что знаки неравенства не всегда указывают на истинное неравенство, иногда они указывают на относительное равенство или другие математические отношения.

Основные понятия в теме «Верное неравенство» включают знаки сравнения (больше, меньше, больше или равно, меньше или равно) и понятие переменной. Переменная представляет число или выражение, которое может принимать различные значения. Например, в неравенстве «x + 3 < 7» переменная «x» может принимать разные значения, и мы должны найти диапазон значений «x», при которых неравенство остается верным.

Примеры неравенств:

• 2x + 5 > 10
• 3y ≤ 15
• 4z + 2 < 6z — 1

В каждом из примеров ученики должны найти диапазон значений переменной, при которых неравенство верно. Это требует применения правил и методов решения неравенств, изучаемых на уроках математики.

Определение неравенства

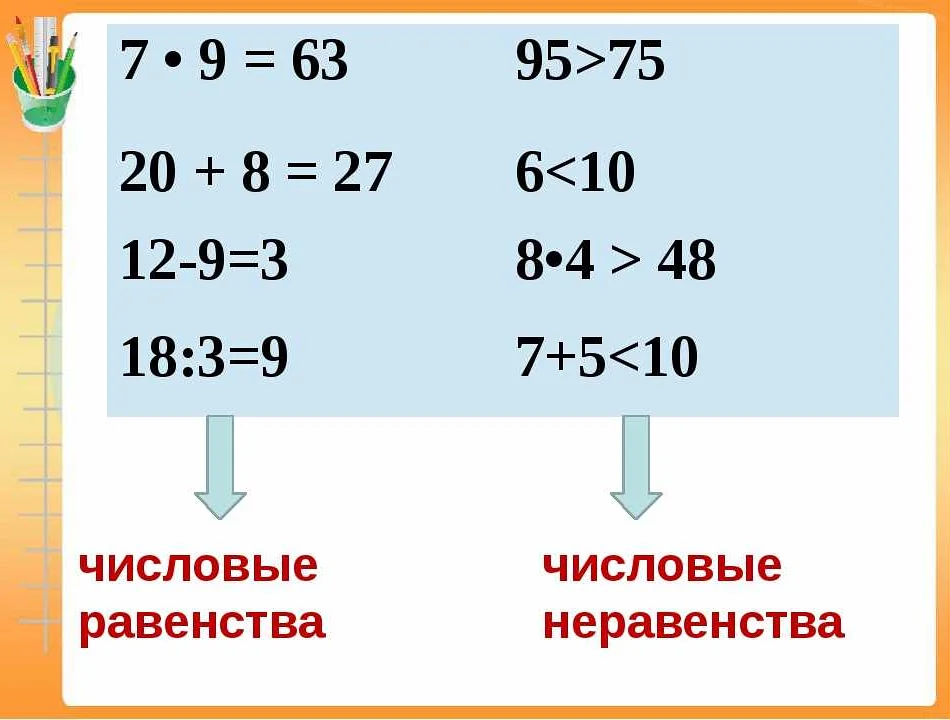
В неравенстве используются следующие знаки сравнения:

ЗнакОписаниеПример

<	Меньше	5 < 8
>	Больше	7 > 3
≤	Меньше или равно	4 ≤ 4
≥	Больше или равно	9 ≥ 6
≠	Не равно	2 ≠ 0

Неравенство можно решить, найдя все значения переменной, которые удовлетворяют данному неравенству.

Сравнение чисел

Для сравнения чисел используются математические знаки:

• Знак больше (>): Если первое число больше второго, то используется знак больше. Например, 5 > 3 – означает, что число 5 больше числа 3.
• Знак меньше ( Если первое число меньше второго, то используется знак меньше. Например, 2 < 7 – означает, что число 2 меньше числа 7.
• Знак равно (=): Если два числа равны, то используется знак равно. Например, 4 = 4 – означает, что число 4 равно числу 4.

При сравнении чисел можно использовать несколько знаков одновременно:

• Знак больше или равно (≥): Если первое число больше или равно второму, то используется знак больше или равно. Например, 5 ≥ 3 – означает, что число 5 больше или равно числу 3.
• Знак меньше или равно (≤): Если первое число меньше или равно второму, то используется знак меньше или равно. Например, 2 ≤ 7 – означает, что число 2 меньше или равно числу 7.

Сравнение чисел – это важная базовая операция, которая применяется в различных областях математики и решении различных задач.

Решение неравенств

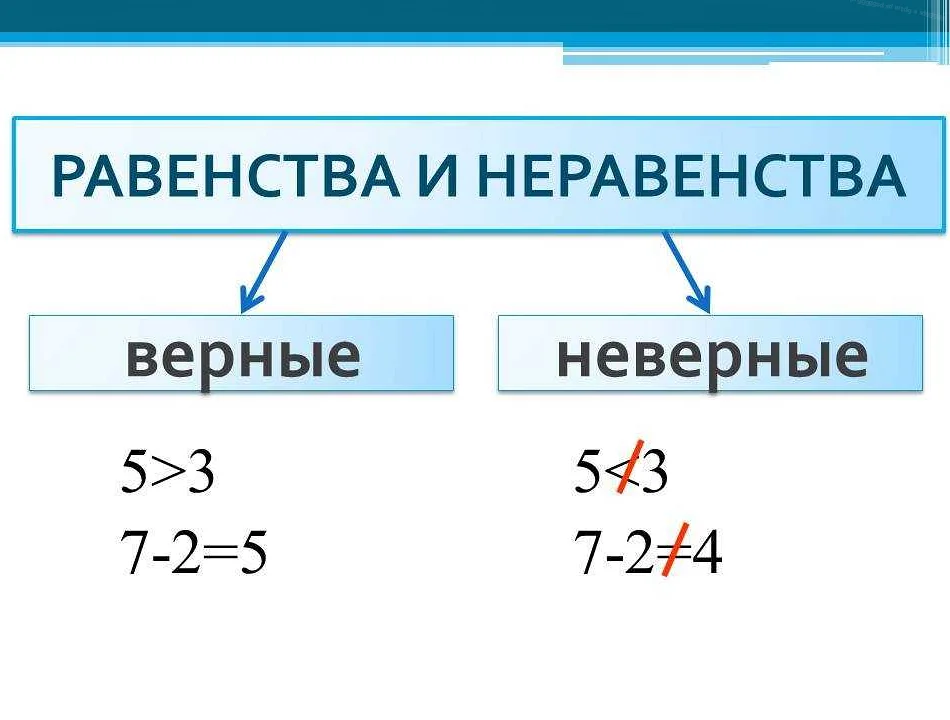
Решение неравенств в математике занимает особое место, так как позволяет определить множество значений переменной, удовлетворяющих заданному условию.

Для решения неравенств существуют определенные правила и методы. В основе решения лежит принцип сохранения знака при изменении стороны неравенства.

Одно из основных правил решения неравенств – это перенос одночлена из одной части неравенства в другую с противоположным знаком.

Например, для неравенства x + 3 > 7 нужно избавиться от слагаемого 3 в левой части, перенося его в правую часть неравенства с противоположным знаком:

x > 7 — 3

x > 4

Таким образом, решением данного неравенства будет множество значений переменной x, больших 4.

Кроме переноса одночлена, существуют и другие методы решения неравенств, такие как деление или умножение обеих частей неравенства на одно и то же положительное число.

Основной прием решения неравенств заключается в определении области допустимых значений переменной, которые удовлетворяют данному неравенству.

При решении неравенств необходимо помнить, что при умножении или делении на отрицательное число знак неравенства меняется на противоположный.

Решение неравенств в математике позволяет найти все допустимые значения переменной, удовлетворяющие заданному условию, и представить их в виде неравенства или интервала.

Таким образом, решение неравенств является важной задачей для определения множества значений переменных в математических моделях и уравнениях.

Операции с неравенствами

Операции с неравенствами позволяют сравнивать и устанавливать отношения между числами.

В математике существуют следующие операции с неравенствами:

ОперацияОбозначениеПримерЗначение

Больше	>	5 > 3	Истина
Меньше	<	2 < 7	Истина
Больше или равно	≥	4 ≥ 4	Истина
Меньше или равно	≤	6 ≤ 9	Истина
Не равно	≠	3 ≠ 3	Ложь

При операциях с неравенствами нужно помнить о следующих правилах:

• Неравенства можно складывать и вычитать, при этом сохраняется знак.
• Неравенства можно умножать и делить на положительное число, при этом сохраняется знак.
• Неравенства можно умножать и делить на отрицательное число, но при этом меняется знак неравенства.
• При умножении или делении на 0 неравенства не сохраняются.

Операции с неравенствами позволяют решать различные задачи, в которых требуется сравнивать и устанавливать отношения между числами.

Неравенства с переменными

Для решения неравенств можно использовать различные приемы. Одним из самых простых и часто используемых способов является графический метод. Для этого строится график неравенства на координатной плоскости и определяется область, где все точки удовлетворяют неравенству.

Например, рассмотрим неравенство 2x + 5 > 10. Для его решения можно построить график прямой y = 2x + 5 и определить область, где значения функции больше 10. В данном случае, это будет полуплоскость над прямой.

Кроме графического метода, неравенства с переменными можно решать алгебраически. Для этого применяются различные арифметические операции, такие как сложение, вычитание, умножение и деление.

Например, пусть дано неравенство 3x — 2 > 10. Чтобы найти значения переменной x, необходимо сначала перенести все слагаемые справа от знака неравенства, получим: 3x > 12. Затем делим обе части неравенства на коэффициент при переменной x, в данном случае 3, получаем: x > 4.

Таким образом, решением данного неравенства является множество всех значений переменной x, больших 4.

Примеры неравенств

Вот несколько примеров неравенств:

Пример неравенстваРешение

x + 5 > 10	x > 5
2y — 3 < 7	y < 5
3z + 4 ≥ 13	z ≥ 3
4a — 2 ≤ 10	a ≤ 3

В этих примерах мы сравниваем выражения и находим значения переменных, при которых неравенства верны.

Помните, что при решении неравенств можно применять те же операции, что и при решении уравнений, но необходимо учитывать знак неравенства и правила сравнения чисел.

Вопрос-ответ:

Какие основные понятия связаны с неравенствами в математике 5 класса?

Основные понятия, связанные с неравенствами в математике 5 класса, включают понятия неравенства, неравенство с переменными, неравенство с числами, и понятие решения неравенства.

Какое верное неравенство можно привести в качестве примера для 5 класса?

Верное неравенство, которое можно привести в качестве примера для 5 класса, — это 2 + 3 > 4.

Как можно решить неравенство с переменными в математике 5 класса?

Неравенство с переменными в математике 5 класса можно решить, используя методы алгебры, такие как приведение подобных слагаемых и умножение или деление на отрицательное число.

Как проверить правильность решения неравенства в математике 5 класса?

Чтобы проверить правильность решения неравенства в математике 5 класса, нужно подставить найденное значение переменной обратно в неравенство и убедиться, что оба выражения с разными знаками остаются верными.

Какие ошибки часто допускают при решении неравенств в математике 5 класса?

При решении неравенств в математике 5 класса часто допускают ошибки, связанные с неправильным применением алгебраических операций, пропуском шагов в решении или неправильной интерпретацией знаков неравенства.

Какие основные понятия связаны с неравенствами в математике?

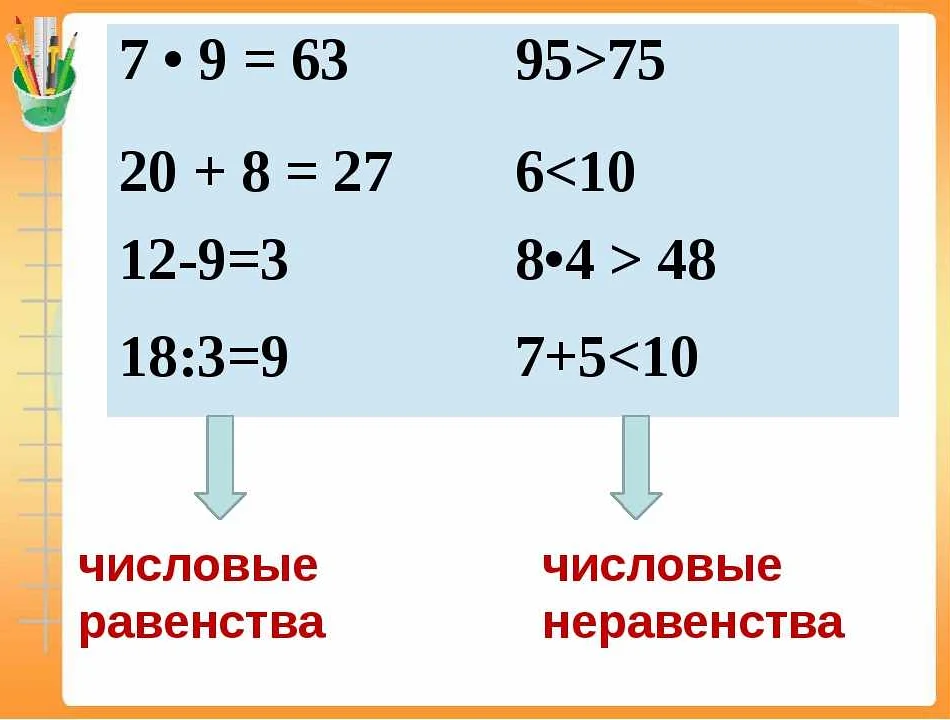
Основные понятия, связанные с неравенствами в математике, это неравенство, знаки сравнения и переменная. Неравенство — это математическое выражение, в котором два числа сравниваются и указывается их отношение (больше, меньше или равно). Знаки сравнения — это символы, которые используются для обозначения отношения между числами (например, > для больше, < для меньше, ≤ для меньше или равно, ≥ для больше или равно). Переменная — это символ, который представляет неизвестное значение и может принимать различные значения в рамках задачи или уравнения.

Видео по теме: