Что сделал эйлер для математики

Математик Леонард Эйлер внес огромный вклад в развитие математики. Он разработал множество новых методов и теорий, открыл новые математические законы и формулы. Узнайте, какие именно открытия сделал Эйлер и как они повлияли на развитие науки.

Леонард Эйлер — выдающийся математик XVIII века, который внес огромный вклад в развитие различных областей математики. Родившись в Швейцарии, Эйлер обладал невероятными способностями к математике с самого детства. Он не только проделал огромную работу в самых разных областях, но и смог сформулировать и доказать множество теорем, которые до сих пор являются основой для многих математических исследований и приложений.

Одним из главных достижений Леонарда Эйлера является разработка и расширение теории функций. Эйлер ввел множество новых обозначений и терминов, которые до сих пор широко используются в математике. Он внес огромный вклад в теорию функций комплексного переменного, разработав множество формул и методов решения различных задач. Благодаря Эйлеру, многие математические объекты и процессы получили формализованные определения и названия, что существенно упростило работу в этой области.

Одним из самых важных открытий Леонарда Эйлера является формула Эйлера, связывающая пять основных математических констант: число е, комплексную единицу i, число π, единицу и нуль. Эта формула имеет огромное значение во многих областях математики и физики и является одной из самых известных формул в мире.

Помимо того, Леонард Эйлер внес значительный вклад в теорию чисел, геометрию, механику и другие области математики. Он разработал методы решения дифференциальных уравнений, установил связь между математикой и физикой, а также решал сложные задачи, связанные с теорией вероятностей и комбинаторикой. Все его открытия и достижения стали основой для дальнейшего развития математики и способствовали прогрессу науки в целом.

Леонард Эйлер оставил неизгладимый след в истории математики своими гениальными открытиями и достижениями. Его вклад в развитие различных областей математики до сих пор оценивается и используется учеными и специалистами по всему миру. Безусловно, Леонард Эйлер является одним из величайших математиков всех времен и научил нас видеть красоту и гармонию в мире чисел и формул.

Жизнь и образование Леонарда Эйлера

Леонард Эйлер, выдающийся математик и физик XVIII века, родился 15 апреля 1707 года в Базеле, в Швейцарии. С самого раннего детства проявил необычайные способности к математике и показал интерес к научным исследованиям.

Он получил первое образование в гимназии города Базеля, где проявил свои таланты в математике и физике. В 1723 году Эйлер поступил в университет Базеля, где изучал философию и теологию, но его настоящей страстью были математика и физика.

В 1726 году Леонард Эйлер переехал в Петербург, где стал членом Академии наук. Здесь он активно занимался исследованиями и публиковал свои первые научные работы. Благодаря своим успехам, Эйлер стал известен не только в России, но и во всей Европе.

В 1733 году Леонард Эйлер переехал в Берлин, где стал членом Прусской академии наук. Здесь он продолжал свои научные исследования и работал над различными областями математики и физики. Эйлер создал многочисленные математические теории и формулы, которые стали основой для дальнейших разработок в этих областях науки.

Леонард Эйлер оставил неизгладимый след в истории математики и физики. Его труды и открытия внесли огромный вклад в развитие этих наук и сформировали основы многих математических и физических теорий.

Дата рождения	15 апреля 1707 года
Место рождения	Базель, Швейцария
Университет	Университет Базеля
Членство	Академия наук (Петербург), Прусская академия наук (Берлин)

Важность работы Леонарда Эйлера в математике

Одним из самых значимых вкладов Леонарда Эйлера в математику является его работа в области анализа. Он развил и систематизировал дифференциальное и интегральное исчисление, сделав их более строгими и обоснованными. Эйлер ввел множество математических понятий и обозначений, которые широко используются и до сих пор. Например, его обозначение e для основания натурального логарифма и i для мнимой единицы.

Также Эйлер сделал важные открытия в теории чисел. Он доказал бесконечность множества простых чисел и разработал методы факторизации и нахождения делителей. Эти результаты имели огромное значение для различных областей математики, включая криптографию и кодирование информации.

В области геометрии Эйлер внес значительный вклад в развитие топологии. Он создал понятие характеристики Эйлера, которая позволяет оценивать форму множества и классифицировать его. Это понятие нашло широкое применение в различных областях, включая географию, физику и биологию.

Необходимо также отметить, что Эйлер является автором множества научных статей и книг, которые стали классикой математической литературы. Он создал удобный формат записи математических формул и использовал его в своих работах. Этот формат, известный как нотация Эйлера, стал стандартом и широко применяется в научных публикациях по всему миру.

Таким образом, вклад Леонарда Эйлера в развитие математики невозможно переоценить. Его открытия и достижения оказали огромное влияние на различные области математики и науки в целом. Работы Эйлера продолжают вдохновлять ученых и студентов по всему миру и оставлять след в современной математике.

Теория чисел: открытия Леонарда Эйлера

Леонард Эйлер сделал значительные вклады в развитие теории чисел, которые оказались революционными для своего времени и стали фундаментом для дальнейших исследований в этой области.

Одно из самых известных открытий Эйлера в теории чисел — это его теорема об обратных элементах. Он доказал, что если два числа являются взаимно простыми, то существует такое число, для которого их произведение даёт остаток 1 при делении на заданное число. Это открытие имело огромное значение для криптографии и криптографических систем, так как позволяло решать задачи, связанные с шифрованием и дешифрованием.

Другим важным достижением Эйлера было его изучение совершенных чисел и их связи с совершенными числами. Он смог доказать, что если число является совершенным, то оно имеет определенный вид, а именно, представляется в виде 2^(p-1) * (2^p — 1), где p и (2^p — 1) — простые числа. Это открытие позволило лучше понять структуру совершенных чисел и их свойства.

Кроме того, Эйлер разработал теорию сравнений, которая позволила ему решать различные задачи, связанные с делимостью чисел. Он ввел понятие остатка от деления и разработал правила и алгоритмы для выполнения операций с остатками. Это позволило ему решать задачи, связанные с простыми числами, факторизацией и нахождением наибольшего общего делителя.

Теория чисел Леонарда Эйлера оказала огромное влияние на развитие математики и имеет применение во многих областях, включая криптографию, компьютерную науку и теорию кодирования. Его открытия и достижения остаются актуальными и востребованными и по сей день.

Исследования в области геометрии и топологии

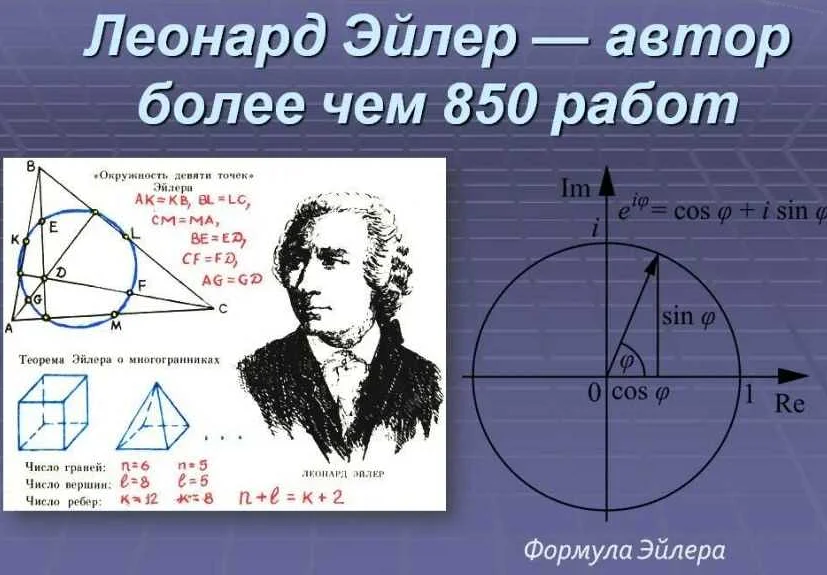
Леонард Эйлер оказал огромное влияние на развитие геометрии и топологии. Он внес значительный вклад в изучение пространственных форм и их свойств.

Одним из ключевых достижений Эйлера в геометрии является его работа в области полиэдральной геометрии. Он разработал формулу Эйлера для полиэдральных сеток, которая связывает количество вершин, ребер и граней. Эта формула стала фундаментальным инструментом в изучении различных классов полиэдров и их свойств.

Эйлер также исследовал топологию поверхностей. Он доказал, что сфера с отверстием неэквивалентна сфере без отверстия, что позволило установить различные топологические свойства поверхностей. Это открытие стало важным шагом в понимании топологии и ее применении в различных областях математики и физики.

Кроме того, Эйлер внес вклад в исследования эллиптических кривых и поверхностей. Он разработал теорию эллиптических функций и уравнений, которая имеет широкое применение в различных областях математики и физики. Его работы в этой области стали основой для дальнейших исследований и развития теории эллиптических функций.

В целом, исследования Леонарда Эйлера в области геометрии и топологии имеют огромное значение для математики. Его открытия и достижения по-прежнему актуальны и востребованы в настоящее время.

Выводы Леонарда Эйлера в области анализа и дифференциальных уравнений

Одним из важнейших выводов Эйлера была формула, которая связывает основные математические константы: число e, число pi, комплексную единицу i и единицу 1. Эта формула, известная как формула Эйлера, имеет вид: e^(i*pi) + 1 = 0. Она объединяет в себе элементы анализа, алгебры и геометрии, и является одним из наиболее известных и красивых математических выражений.

Эйлер также работал над развитием теории функций и провел множество исследований в области экстремумов функций. Он разработал метод дифференциального исчисления, который позволяет находить максимумы и минимумы функций. Этот метод широко применяется в современной математике, физике и других науках.

Одним из самых важных достижений Эйлера в области дифференциальных уравнений является его решение уравнения, известного как уравнение Эйлера-Лагранжа. Это уравнение является основой для принципа наименьшего действия, который играет ключевую роль в физике и механике. Решение уравнения Эйлера-Лагранжа позволяет находить оптимальные пути и траектории для систем с переменными параметрами.

Кроме того, Эйлер внес значительный вклад в развитие теории дифференциальных уравнений. Он разработал метод решения линейных дифференциальных уравнений с постоянными коэффициентами, который стал основой для дальнейших исследований в этой области. Эйлер также внес важные вклады в развитие численных методов решения дифференциальных уравнений.

Выводы и открытия Леонарда Эйлера в области анализа и дифференциальных уравнений сыграли решающую роль в развитии математики. Его работы оказали огромное влияние на последующие поколения математиков и продолжают использоваться и изучаться до сегодняшнего дня.

Влияние Леонарда Эйлера на развитие физики

Леонард Эйлер был не только выдающимся математиком, но и оказал значительное влияние на развитие физики. Его работы и открытия в области математики имели применение и в физических науках, что сделало его одним из важнейших фигур в истории науки.

Одним из наиболее значимых вкладов Леонарда Эйлера в физику стала его работа в области механики. Он разработал основы аналитической механики, в частности, принципы, лежащие в основе закона сохранения энергии и движения тела по инерции. Эти принципы были важными шагами в развитии классической механики и сыграли ключевую роль в построении общей теории относительности Альберта Эйнштейна.

Кроме того, Леонард Эйлер внес значительный вклад в развитие оптики и электромагнетизма. Он исследовал распространение света, разработал формулы для определения фокусного расстояния линз и провел исследования в области дифракции и интерференции света. Эти работы были важными шагами в понимании природы света и привели к развитию современной оптики.

Также Леонард Эйлер внес вклад в развитие термодинамики. Он исследовал законы теплопроводности и разработал формулы для расчета теплопроводности в различных материалах. Эти исследования помогли установить основные принципы термодинамики и стали основой для развития современной теплофизики.

Таким образом, Леонард Эйлер внес огромный вклад в развитие физики. Его работы и открытия в области математики оказали влияние на различные области физических наук и способствовали развитию современной науки.

Эйлер и теория вероятностей

Леонард Эйлер внес значительный вклад в развитие теории вероятностей. Его работы в этой области оказали огромное влияние на развитие математики и статистики.

Эйлер разработал основные понятия и методы теории вероятностей, включая вероятность события, условную вероятность, независимость событий и комбинаторику.

Одним из самых значимых достижений Эйлера в теории вероятностей является его работа над теорией больших чисел. Он сформулировал закон больших чисел, который позволяет описать поведение среднего значения случайной величины при увеличении числа испытаний. Этот закон стал одним из фундаментальных принципов современной вероятностной теории.

Благодаря своим исследованиям, Эйлер смог дать математическое обоснование многим практическим примерам, связанным с вероятностными явлениями. Он разработал методы расчета вероятности различных событий, а также приложил их к задачам из физики, статистики и других областей.

Эйлер также внес важный вклад в развитие теории игр, которая тесно связана с теорией вероятностей. Он исследовал вероятностные аспекты различных стратегий игр и сформулировал основные принципы оптимальных стратегий.

В целом, вклад Леонарда Эйлера в развитие теории вероятностей был огромным. Его работы стали отправной точкой для дальнейшего развития этой области математики и оказали значительное влияние на современные теоретические и прикладные исследования.

Вопрос-ответ:

Какой вклад в развитие математики внес Леонард Эйлер?

Леонард Эйлер внес огромный вклад в развитие математики. Он считается одним из самых великих математиков всех времен. Его достижения включают разработку теории функций, теории чисел, анализа, теории графов и множество других областей математики.

Какие гениальные открытия сделал Леонард Эйлер?

Леонард Эйлер сделал множество гениальных открытий. Он разработал основы дифференциального и интегрального исчисления, ввел понятие функции и разработал теорию функций. Он также сделал открытия в области комбинаторики, геометрии, теории чисел и многих других областей математики.

Какие достижения Леонарда Эйлера считаются самыми значимыми?

Самыми значимыми достижениями Леонарда Эйлера считаются его работы в области дифференциального и интегрального исчисления, а также его вклад в разработку теории чисел. Он также сделал множество других важных открытий, включая разработку теории графов и введение понятия функции.

Какие области математики были развиты благодаря Леонарду Эйлеру?

Благодаря Леонарду Эйлеру были развиты множество областей математики. Он сделал значительный вклад в разработку дифференциального и интегрального исчисления, теории чисел, теории графов, комбинаторики и множество других областей. Его работы оказали огромное влияние на развитие математики в целом.

Почему Леонард Эйлер считается одним из величайших математиков?

Леонард Эйлер считается одним из величайших математиков, потому что его работу можно считать основой многих современных областей математики. Его открытия и достижения в области дифференциального и интегрального исчисления, теории чисел, теории графов и многих других областей имеют огромное значение для современной математики.

Наследие Леонарда Эйлера в современной математике

Одним из наиболее значимых вкладов Леонарда Эйлера в современную математику является его работа в области математического анализа. Он развил теорию функций и доказал множество теорем, которые по сей день используются в исследовании функций и их свойств. Эйлер впервые ввел понятие экспоненты и натурального логарифма, которые стали основой для развития математического анализа и математической физики.

Кроме того, Леонард Эйлер внес огромный вклад в развитие теории чисел. Он изучал различные свойства простых чисел, исследовал их распределение и взаимосвязь с другими математическими объектами. Эйлер открыл множество новых числовых последовательностей, формул и закономерностей, которые до сих пор изучаются и применяются в современной математике.

Также стоит отметить вклад Леонарда Эйлера в развитие графовой теории. Он сформулировал и доказал множество теорем, связанных с графами, и внес значительные улучшения в методы их исследования. Эйлер разработал алгоритмы для нахождения путей и циклов в графах, что имело огромное значение для развития информатики и теории вычислений.

В целом, наследие Леонарда Эйлера в современной математике трудно переоценить. Его открытия и достижения стали фундаментом для многих областей науки, и до сих пор используются и развиваются учеными по всему миру. Эйлер оказал огромное влияние на развитие математики, и его наследие продолжает вдохновлять исследователей и математиков на новые открытия и достижения.

Видео по теме: