ОГЭ по математике: какие задания по геометрии встречаются на экзамене
Содержимое
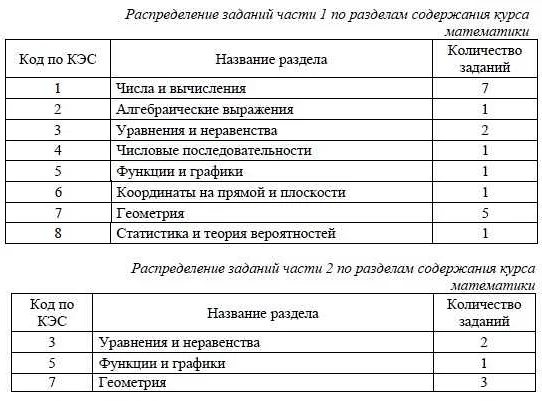
- 1 ОГЭ по математике: какие задания по геометрии встречаются на экзамене
- 1.1 Основные темы геометрии для ОГЭ по математике
- 1.2 Видео по теме:
- 1.3 Свойства фигур на плоскости
- 1.4 Формулы для нахождения площади и периметра геометрических фигур
- 1.5 Вопрос-ответ:
- 1.5.0.1 Какие основные темы геометрии рассматриваются на ОГЭ по математике?
- 1.5.0.2 Каковы требования к решению задач геометрии на ОГЭ?
- 1.5.0.3 Какие ошибки чаще всего допускаются при решении задач геометрии на ОГЭ?
- 1.5.0.4 Как можно улучшить свои знания по геометрии для подготовки к ОГЭ?
- 1.5.0.5 Какие трудности могут возникнуть при решении задач по геометрии на ОГЭ?
- 1.5.0.6 Как сократить время на решение задач по геометрии на ОГЭ?
- 1.5.0.7 Существуют ли какие-то секреты успешной подготовки к геометрии на ОГЭ?
- 1.6 Треугольники: виды, свойства, формулы
- 1.7 Окружности: свойства, формулы для рассчета площади и длины дуги
- 1.8 Теорема Пифагора и применение ее в задачах
- 1.9 Равенство треугольников и его свойства
- 1.10 Равнобедренные и равносторонние треугольники: свойства и формулы
- 1.11 Прямоугольные треугольники: свойства и формулы
- 1.12 Параллелограммы: свойства и формулы для нахождения площади и периметра
- 1.13 Трапеции: свойства и формулы для нахождения площади
- 1.14 Задачи на конструирование фигур
Узнайте, какие темы геометрии входят в задания на ОГЭ по математике и как подготовиться к успешной сдаче экзамена. Подробный анализ типичных заданий и рекомендации для учеников.
Задания по геометрии являются одними из самых важных на ОГЭ по математике. Это область математики, которая изучает отношения между фигурами в пространстве и плоскости. Понимание основных тем геометрии — это ключ к успешному решению задач на экзамене.
Среди основных тем геометрии, которые могут быть представлены на ОГЭ, находятся: прямоугольники и квадраты, треугольники, круги, пирамиды, прямые и углы.
Решение задач по геометрии требует от ученика не только навыков расчетов, но и способности к абстрактному мышлению и умению находить простые способы решения сложных задач.
В данной статье мы рассмотрим основные темы геометрии, которые могут встретиться на ОГЭ по математике, а также дадим советы по их успешному решению.
Основные темы геометрии для ОГЭ по математике
В рамках ОГЭ по математике одной из основных тем является геометрия. В процессе подготовки необходимо тщательно изучить все ее аспекты для успешной сдачи экзамена.
Геометрия включает в себя множество понятий, таких как лучи, прямые, отрезки, углы, плоскости, грани и тела. Необходимо понимать и уметь применять данные термины в решении задач на ОГЭ.
Кроме этого, важно знать формулы для вычисления площадей, объемов и периметров различных фигур. В их числе: треугольников, прямоугольников, кругов, трапеций, параллелограммов и других.
Также в рамках геометрии на ОГЭ по математике могут быть задачи на подобие фигур, нахождение высот и длин отрезков на плоскости, а также построение графиков.
Важно понимать, что геометрические задачи на ОГЭ часто требуют не только знания формул и теоретических основ, но и умения «видеть» в геометрических фигурах их свойства и закономерности. Это поможет не только в успешном решении задач, но и в общем развитии математического мышления.
Итак, геометрия – это одна из основных тем ОГЭ по математике. Важно тщательно изучить все ее аспекты и научиться применять их для успешного сдачи экзамена.
Видео по теме:
Свойства фигур на плоскости
Треугольники:
- Сумма углов в треугольнике равна 180 градусам
- Стороны треугольника могут быть равными или неравными
- Высота, опущенная на сторону, является перпендикуляром к этой стороне и делит треугольник на две равные части
- Медиана, проведенная к стороне, является отрезком, соединяющим вершину треугольника с серединой этой стороны.
Прямоугольники:
- Углы между противоположными сторонами прямоугольника прямые (90 градусов)
- Противоположные стороны прямоугольника равны между собой
- Диагонали прямоугольника равны между собой и делят прямоугольник на два равных треугольника
Круги:
- Центр круга — точка, равноудаленная от всех точек на окружности круга
- Радиус — отрезок, соединяющий центр круга с точкой на окружности
- Диаметр — отрезок, проходящий через центр круга и ограничивающийся на его окружности точками
- Длина окружности круга равна произведению диаметра на число Пи (3,14)
Многоугольники:
- Сумма углов в многоугольнике равна произведению количества его сторон на 180 градусов минус 360 градусов (для многоугольника с n сторонами: 180 * n — 360)
- Многоугольник с n сторонами можно разрезать на n-2 треугольника
Формулы для нахождения площади и периметра геометрических фигур
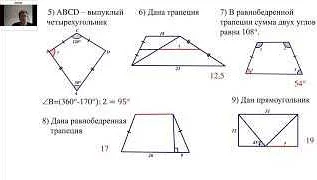
Геометрия – одна из самых важных разделов математики, связанная с исследованием фигур, их основных характеристик и взаимоотношений. Для решения задач по этому предмету необходимо знать основные формулы для нахождения площади и периметра геометрических фигур.
Например, для вычисления площади треугольника можно использовать формулу: S = 0.5 * a * h, где S – площадь, a – длина основания, h – высота.
Для расчета периметра треугольника нужно сложить длины всех его сторон: P = a + b + c, где P – периметр, a, b, c – длины сторон.
Другие примеры формул:
- для площади круга: S = π * r², где S – площадь, r – радиус, π ≈ 3.14;
- для периметра квадрата: P = 4a, где P – периметр, a – длина стороны;
- для площади прямоугольника: S = a * b, где S – площадь, a, b – длины сторон;
- для периметра окружности: P = 2πr, где P – периметр, r – радиус, π ≈ 3.14.
Знание формул для нахождения площади и периметра геометрических фигур является необходимым при выполнении заданий на ОГЭ по математике. Поэтому необходимо хорошо изучать эту тему и не забывать повторять полученные знания.
Вопрос-ответ:
Какие основные темы геометрии рассматриваются на ОГЭ по математике?
На ОГЭ по математике рассматриваются такие основные темы геометрии, как понятия прямой, угла, треугольника, четырехугольника, окружности, круга, геометрические тела, пространственные отношения между фигурами.
Каковы требования к решению задач геометрии на ОГЭ?
При решении задач геометрии на ОГЭ необходимо уметь правильно читать условие задачи, использовать свои знания по геометрии, оценивать результаты вычислений и проверять решение. Также необходимо уметь работать с геометрическими построениями и использовать их для решения задач.
Какие ошибки чаще всего допускаются при решении задач геометрии на ОГЭ?
Чаще всего при решении задач геометрии на ОГЭ допускаются следующие ошибки: неправильное чтение условия задачи, неправильное использование формул и правил геометрии, неверное решение простейших алгебраических уравнений и неправильное построение геометрических фигур.
Как можно улучшить свои знания по геометрии для подготовки к ОГЭ?
Для улучшения знаний по геометрии для подготовки к ОГЭ необходимо решать задачи по геометрии и изучать геометрические построения. Также полезно прочитать учебник по математике и изучить основные геометрические понятия, формулы и правила. Можно также посещать курсы подготовки к ОГЭ, где будут изучаться основные темы для экзамена.
Какие трудности могут возникнуть при решении задач по геометрии на ОГЭ?
При решении задач по геометрии на ОГЭ могут возникнуть трудности в правильном понимании условия задачи, определении необходимых данных и правильном использовании формул и правил геометрии. Также могут возникнуть трудности при работе с геометрическими построениями и определении относительных положений фигур.
Как сократить время на решение задач по геометрии на ОГЭ?
Для сокращения времени на решение задач геометрии на ОГЭ можно использовать геометрические построения и относительные положения фигур. Также необходимо уметь работать с формулами и правилами геометрии и искать упрощенные методы решения задач. Важно также не зацикливаться на одной задаче, а переходить к следующей, если текущая занимает слишком много времени.
Существуют ли какие-то секреты успешной подготовки к геометрии на ОГЭ?
Одним из секретов успешной подготовки к геометрии на ОГЭ является регулярное решение задач и повторение геометрических формул и правил. Также важно уметь быстро читать условия задач и делать правильные выводы. Необходимо также уметь работать с краткими и точными записями и пользоваться графическими построениями. Однако наиболее важным секретом является практика и репетитивность, которые позволяют глубже изучить материал и привыкнуть к экзаменационной ситуации.
Треугольники: виды, свойства, формулы
Треугольник — это геометрическая фигура, состоящая из трех сторон и трех углов. По форме и размерам треугольники могут быть разных видов. Существует несколько классификаций треугольников:
- По длинам сторон: равносторонний, равнобедренный, разносторонний;
- По величине углов: остроугольный, тупоугольный, прямоугольный;
- По расположению: прямоугольный, наклонный, подобный.
Свойства треугольников:
- Сумма внутренних углов треугольника равна 180 градусам;
- Сторона треугольника всегда меньше суммы двух других сторон и больше разности между ними;
- Высота опущенная на сторону лежит внутри треугольника и является перпендикуляром к этой стороне;
- Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны и проходящий через центр тяжести треугольника;
- Биссектриса — отрезок, который делит угол треугольника на два равных угла и пересекает противоположную сторону под прямым углом.
Формулы для нахождения площади треугольника:
- Площадь равностороннего треугольника равна квадратному корню из трех, деленному на 4 и умноженному на квадрат длины стороны;
- Площадь произвольного треугольника можно вычислить по формуле Герона: S = √(p(p-a)(p-b)(p-c)), где p — полупериметр, a, b, c — длины сторон;
- Если известны длины основания и высоты треугольника, то площадь можно найти по формуле S = 1/2 * b * h.
Окружности: свойства, формулы для рассчета площади и длины дуги
Окружность — это геометрическая фигура, состоящая из всех точек, равноудаленных от центра. Она имеет множество интересных свойств. Каждая окружность имеет диаметр — отрезок, соединяющий две точки на окружности и проходящий через ее центр. Длина диаметра равна удвоенному радиусу — расстоянию от центра до любой точки на окружности.
Еще одно важное понятие — длина окружности, равная произведению радиуса на число π (примерно 3,14). Это число является константой для любой окружности и используется для расчетов площади и длины дуги.
Формулы для расчета площади и длины дуги:
- Площадь круга: S = πr2, где r — радиус окружности.
- Длина окружности: L = 2πr
- Длина дуги: Larc = θ/360° × 2πr, где θ — центральный угол, отвечающий за дугу.
Заметим, что длина дуги зависит от центрального угла. Так, если θ = 360° (или 2π), то длина дуги равна длине окружности, а если θ = 180° (или π), то длина дуги будет половиной длины окружности.
В задачах на ОГЭ по математике часто используются задачи на вычисление площади круга, длины окружности и длины дуги. Необходимо помнить основные формулы и уметь правильно подставлять значения.
Теорема Пифагора и применение ее в задачах
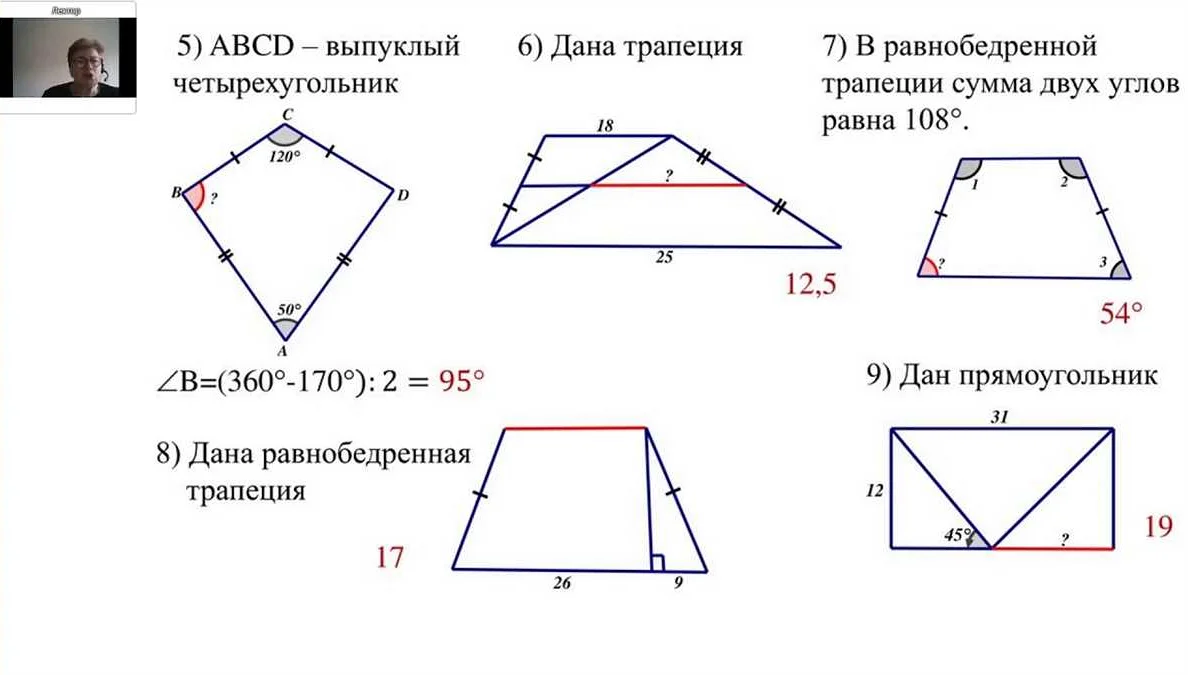
Теорема Пифагора является одной из основных теорем геометрии и формулируется так: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Если обозначить длину гипотенузы через с и длины катетов через a и b соответственно, то формула теоремы Пифагора выглядит следующим образом: c² = a² + b².
Теорема Пифагора широко применяется в задачах получения длины стороны треугольника. Для решения таких задач необходимо использовать известные значения двух сторон и вычислить третью, применяя теорему Пифагора.
Например, если известны длины катетов прямоугольного треугольника a = 3 см и b = 4 см, то можно вычислить длину гипотенузы с помощью теоремы Пифагора: c² = 3² + 4², c² = 9 + 16, c = √25, c = 5 см.
Возможно также использование теоремы Пифагора для проверки прямоугольности треугольника. Если известны длины трех сторон треугольника a, b и c, то можно применить теорему Пифагора: если с² = a² + b² или а² = с² — b² или b² = с² — а², то треугольник является прямоугольным.
Равенство треугольников и его свойства
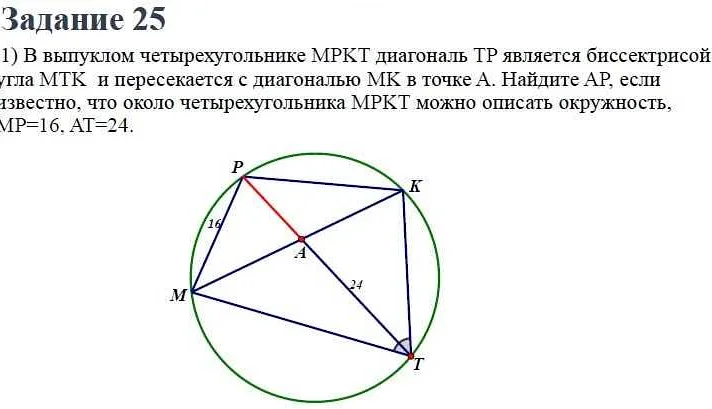
Равенство треугольников — это основное свойство геометрии, которое утверждает, что если у двух треугольников соответственные стороны и прилежащие углы равны, то эти треугольники равны между собой.
Существует несколько способов доказательства равенства треугольников. Один из них — это метод SSS (сторона-сторона-сторона), который означает, что если три стороны одного треугольника равны соответствующим сторонам другого треугольника, то эти треугольники равны.
Еще один метод — это метод SAS (сторона-угол-сторона), который утверждает, что если две стороны одного треугольника и угол между ними равны соответствующим сторонам и углу другого треугольника, то эти треугольники равны.
Третий метод — это метод ASA (угол-сторона-угол), гласящий, что если два угла одного треугольника и сторона между ними равны соответствующим углам и стороне другого треугольника, то эти треугольники равны.
Равенство треугольников позволяет решать многие задачи геометрии, в том числе, определять длины сторон и углы треугольников по данным значениям других треугольников.
- SSS (сторона-сторона-сторона) — три стороны одного треугольника равны соответствующим сторонам другого треугольника;
- SAS (сторона-угол-сторона) — две стороны одного треугольника и угол между ними равны соответствующим сторонам и углу другого треугольника;
- ASA (угол-сторона-угол) — два угла одного треугольника и сторона между ними равны соответствующим углам и стороне другого треугольника;
- AAS (угол-угол-сторона) — два угла одного треугольника и сторона, не являющаяся стороной между этими углами, равны соответствующим углам и стороне другого треугольника.
Равенство треугольников предоставляет нам возможность решать множество задач геометрии с помощью применения соответствующих методов доказательства равенства треугольников.
Равнобедренные и равносторонние треугольники: свойства и формулы

Равнобедренный треугольник — это треугольник, у которого две стороны равны. Аналогично, равносторонний треугольник — это треугольник, у которого все стороны равны.
Свойства равнобедренного треугольника:
- Биссектриса угла, прилегающего к основанию, делит угол пополам и перпендикулярна основанию.
- Высота, проведенная к основанию, является медианой и медиатрисой.
- Окружность, описанная вокруг равнобедренного треугольника, проходит через вершину, лежащую на стороне основания, а также через середину основания.
- Равнобедренный треугольник может быть разделен на два равных прямоугольных треугольника.
Свойства равностороннего треугольника:
- Углы равностороннего треугольника равны между собой и равны 60 градусов.
- Высота, проведенная из вершины к основанию, является медианой, биссектрисой и медиатрисой.
- Равносторонний треугольник может быть разделен на три равных равнобедренных треугольника.
- Площадь равностороннего треугольника равна: S=(a^2√3)/4, где a — длина стороны треугольника.
Прямоугольные треугольники: свойства и формулы
Прямоугольный треугольник – это треугольник, у которого один из углов равен 90 градусам. Такой угол называется прямым углом, а его сторона – гипотенузой.
Свойства прямоугольных треугольников:
- Катеты треугольника в квадрате равны сумме квадратов гипотенузы. Это называется теоремой Пифагора: a2 + b2 = c2, где a и b – катеты, c – гипотенуза.
- Угол между катетами прямоугольного треугольника равен 90 градусам.
- Катеты прямоугольного треугольника являются половинами гипотенузы, если на гипотенузу опущена высота.
- Высота прямоугольного треугольника, опущенная на гипотенузу, является средним гармоническим между отрезками гипотенузы, на которые эта высота делит гипотенузу.
Формулы для нахождения сторон и углов прямоугольного треугольника:
- Синус угла: sin α = a/c, sin β = b/c, где α и β – углы, a и b – катеты, c – гипотенуза.
- Косинус угла: cos α = b/c, cos β = a/c, где α и β – углы, a и b – катеты, c – гипотенуза.
- Тангенс угла: tg α = a/b, tg β = b/a, где α и β – углы, a и b – катеты.
- Катет: a = c*sin α, b = c*sin β.
- Гипотенуза: c = √(a2+b2).
Правильное использование формул и знание свойств прямоугольных треугольников помогает решить многие задачи на ОГЭ по математике.
Параллелограммы: свойства и формулы для нахождения площади и периметра
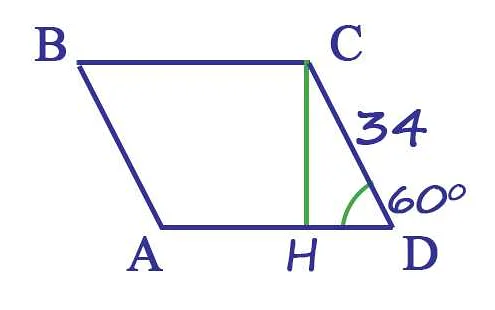
Свойства параллелограмма:
- Противоположные стороны параллельны.
- Противоположные углы равны.
- Сумма углов параллелограмма равна 360°.
- Диагонали параллелограмма делятся пополам.
Формулы для нахождения площади и периметра параллелограмма:
- Периметр P = 2(a + b), где a и b — длины двух параллельных сторон.
- Площадь S = a*h, где a — длина основания параллелограмма, h — высота, проведенная к основанию.
Также существует формула для нахождения высоты h, если известны длины сторон и угол между ними:
h = a*sin(α), где α — угол между длинными сторонами.
Пример задания на нахождение площади и периметра параллелограмма:
Дан параллелограмм ABCD, где AB = 6 см, BC = 8 см, угол между сторонами AB и BC равен 60°. Найдите площадь и периметр параллелограмма.
Решение:
Найдем длину стороны CD, зная, что противоположные стороны параллельны: CD = AB = 6 см. Найдем высоту h, используя формулу высоты: h = AB*sin(60°) = 3√3 см.
Теперь можем найти площадь, используя формулу для площади параллелограмма: S = AB*h = 6*3√3 см² ≈ 31.2 см²
И периметр, используя формулу для периметра параллелограмма: P = 2(AB + BC) = 2(6 + 8) см = 28 см.
Трапеции: свойства и формулы для нахождения площади
Трапеция – это четырехугольник, у которого есть пара параллельных сторон. Основания трапеции – это пара параллельных сторон, а боковые стороны – это две оставшиеся стороны, которые не параллельны.
Свойства трапеции:
- Сумма всех углов трапеции равна 360 градусам.
- Сторона, перпендикулярная основаниям трапеции, называется высотой.
- Высоты, опущенные на основания трапеции, равны между собой.
- Сумма длин оснований умноженная на высоту равна удвоенной площади трапеции.
Формула для нахождения площади трапеции:
S = (a + b) * h / 2
где a и b – длины оснований трапеции, а h – высота, опущенная на основания.
Если известны длины оснований и высоты, то для нахождения площади трапеции достаточно вставить значения в формулу. Если же известны только длины боковых сторон и одного из оснований, то площадь можно найти по следующей формуле:
S = ((a + b) / 2) * c
где c – длина боковой стороны, параллельной основаниям.
Пример:
Дана трапеция ABCD с основаниями AB = 12 и CD = 5, а также высотой h = 8. Найти площадь трапеции.
S = (a + b) * h / 2 = (12 + 5) * 8 / 2 = 68
Ответ: 68
Задачи на конструирование фигур
В задачах на конструирование фигур требуется на плоскости или в пространстве построить фигуру заданного вида, используя компас и линейку. Обычно в таких задачах нужно построить треугольник, круг, равнобедренную трапецию или другую геометрическую фигуру, зная её геометрические параметры или свойства.
Одной из наиболее часто встречающихся задач на конструирование является задание на построение равностороннего треугольника. Для этого необходимо провести окружность с центром в заданной точке, а затем, используя компас и линейку, построить на данной окружности треугольник со сторонами равными её радиусу.
Еще одной типичной задачей на конструирование является задание на построение круга, проходящего через три заданные точки на плоскости. Для решения этой задачи необходимо провести через заданные точки две прямые и найти точку пересечения, которая будет центром круга. Затем, используя компас, необходимо провести круг с заданным радиусом и центром в найденной точке.
Важным навыком при решении задач на конструирование является умение работать с геометрическими построениями и свойствами фигур. Для того чтобы успешно решать задачи на конструирование, необходимо знать основные понятия и формулы геометрии, а также иметь опыт работы с компасом и линейкой.