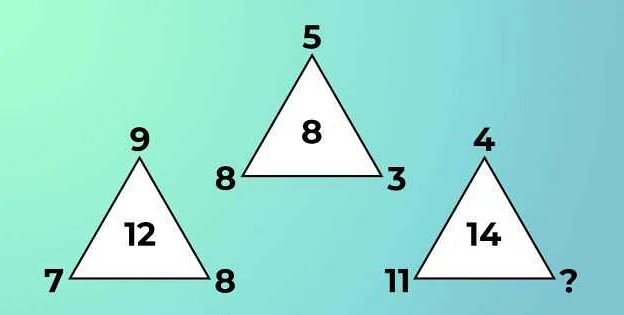
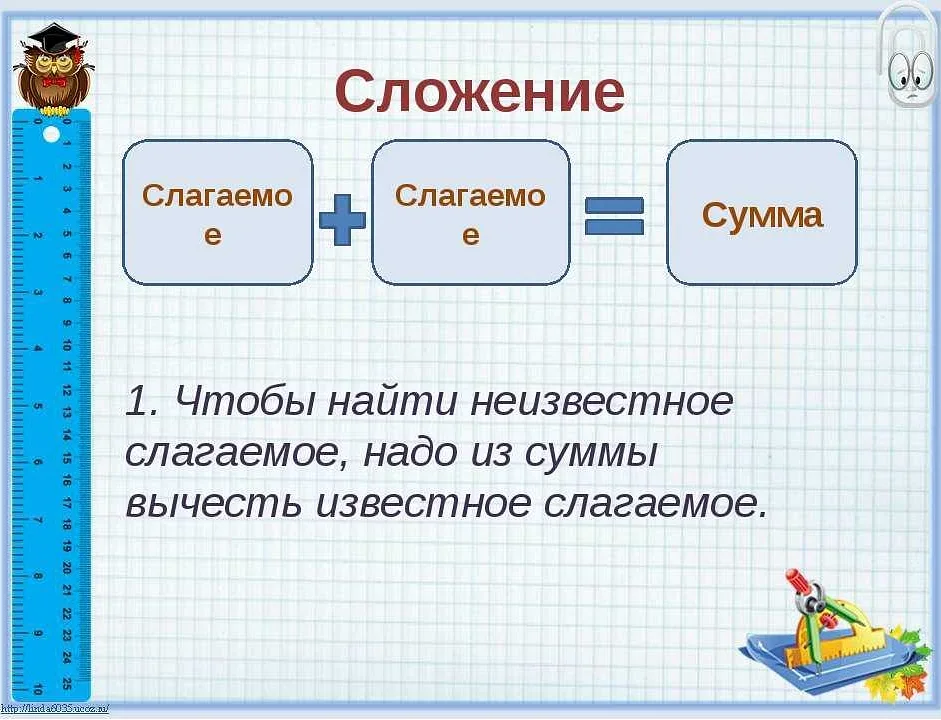
Что такое закономерность в математике 3 класс

Что такое закономерность в математике 3 класс? Узнайте, как закономерности помогают ученикам развивать логическое мышление и навыки решения задач. Познакомьтесь с примерами и объяснениями закономерностей в математике для третьего класса.

Закономерность – это особое свойство числовых последовательностей, которое позволяет нам предсказывать значения следующих чисел. В математике закономерность является важным инструментом для анализа числовых рядов и решения различных задач.

Учебная программа для 3 класса предусматривает изучение закономерностей числовых рядов. Этот раздел математики помогает развить у детей логическое мышление, умение анализировать числовые последовательности и находить их закономерности.

Примером простой закономерности может служить увеличение чисел на 2. Например, 2, 4, 6, 8, 10, 12 и так далее. В этом случае каждое следующее число в ряду больше предыдущего на 2.

Другой пример закономерности – умножение чисел на 3. Например, 1, 3, 9, 27, 81, 243 и т.д. В этом случае каждое следующее число в ряду получается путем умножения предыдущего числа на 3.

Закономерности могут быть различными и более сложными. Они могут быть заданы не только арифметическими или геометрическими прогрессиями, но и другими математическими формулами. Изучение закономерностей помогает детям улучшить свои навыки решения математических задач и применять их в повседневной жизни.

Что такое закономерность в математике?

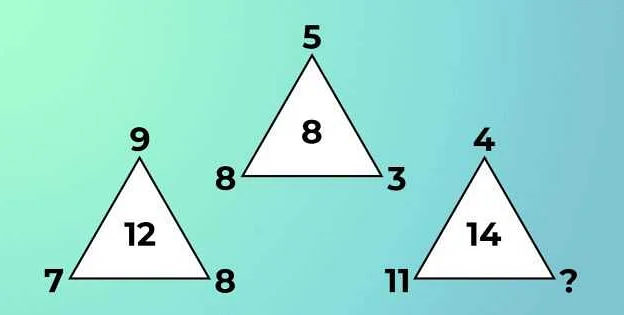
В математике понятие закономерности связано с определенными свойствами чисел или объектов, которые повторяются при определенных условиях. Закономерность может проявляться в последовательности чисел, геометрических фигурах, операциях и других математических объектах.

Закономерность в математике позволяет нам выявить и описать закономерные изменения и связи между числами или объектами. Она помогает нам прогнозировать значения, находить закономерности в данных и делать обобщения.

Примеры закономерностей в математике:

ЗакономерностьПример

Арифметическая прогрессия	2, 4, 6, 8, 10, …
Геометрическая прогрессия	3, 6, 12, 24, 48, …
Факториал числа	0! = 1, 1! = 1, 2! = 2, 3! = 6, 4! = 24, …
Закономерность в таблице умножения	1 × 1 = 1, 2 × 1 = 2, 3 × 1 = 3, …

Знание закономерностей в математике помогает нам решать задачи, находить общую формулу и делать выводы на основе имеющихся данных. Это важный элемент в изучении и понимании математических концепций и принципов.

Определение и понятие

Закономерности могут быть различных типов. Например, арифметическая закономерность — это последовательность чисел, в которой каждый следующий элемент получается путем прибавления одного и того же числа к предыдущему. Например, 2, 4, 6, 8, 10 — это арифметическая закономерность с шагом 2.

Геометрическая закономерность — это последовательность чисел, в которой каждый следующий элемент получается путем умножения предыдущего на одно и то же число. Например, 2, 6, 18, 54 — это геометрическая закономерность с множителем 3.

Для понимания закономерностей в математике ребенку необходимо уметь выделять общую связь между элементами последовательности и определять шаг или множитель. Понимание и использование закономерностей помогает ребенку решать математические задачи, а также развивает его логическое мышление и аналитические способности.

Закономерность в математике: примеры

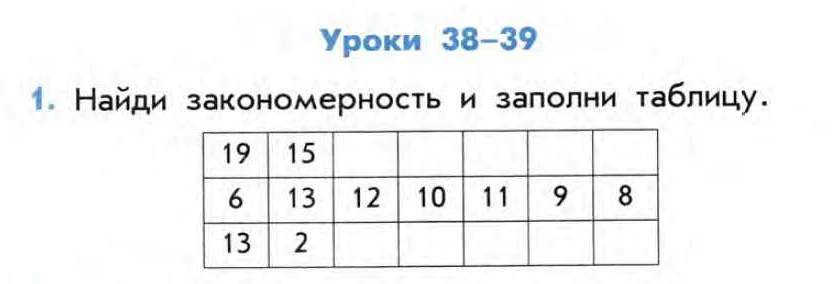
Примером закономерности может служить арифметическая прогрессия. В арифметической прогрессии каждый следующий элемент получается прибавлением одного и того же числа (шага) к предыдущему элементу. Например, рассмотрим арифметическую прогрессию: 2, 5, 8, 11, 14… Здесь шаг равен 3, то есть каждый следующий элемент на 3 больше предыдущего.

Еще одним примером закономерности может быть геометрическая прогрессия. В геометрической прогрессии каждый следующий элемент получается умножением предыдущего элемента на одно и то же число (знаменатель). Например, рассмотрим геометрическую прогрессию: 3, 6, 12, 24, 48… Здесь знаменатель равен 2, то есть каждый следующий элемент в два раза больше предыдущего.

Также в математике есть закономерности, основанные на свойствах числовых рядов, фигур и геометрических фигур, алгебраических формул и т. д. Изучение закономерностей позволяет увидеть и понять порядок и логику в математических явлениях и решать задачи более эффективно.

Пример 1: Арифметическая прогрессия

Например, рассмотрим арифметическую прогрессию, в которой первый элемент равен 3, а шаг прогрессии равен 2. Тогда следующие элементы прогрессии будут: 5, 7, 9, 11 и так далее.

Формула для нахождения любого элемента арифметической прогрессии:

an = a1 + (n — 1)d

где an — n-й элемент прогрессии, a1 — первый элемент прогрессии, n — номер элемента прогрессии, d — шаг прогрессии.

Таким образом, с помощью формулы можно находить любой элемент арифметической прогрессии, зная первый элемент и шаг прогрессии.

Пример 2: Геометрическая прогрессия

an = a1 * q(n-1)

где:

• an — n-й член геометрической прогрессии
• a1 — первый член геометрической прогрессии
• q — знаменатель прогрессии
• n — номер члена геометрической прогрессии

Например, рассмотрим геометрическую прогрессию с первым членом 2 и знаменателем 3. Чтобы найти пятый член этой прогрессии, подставим значения в формулу:

nan

1	2
2	2 * 3(2-1) = 6
3	2 * 3(3-1) = 18
4	2 * 3(4-1) = 54
5	2 * 3(5-1) = 162

Таким образом, пятый член геометрической прогрессии с первым членом 2 и знаменателем 3 равен 162.

Пример 3: Последовательность нечетных чисел

Рассмотрим последовательность чисел, в которой каждое следующее число больше предыдущего на 2. Такая последовательность называется последовательностью нечетных чисел. Начнем с числа 1 и будем прибавлять к предыдущему числу 2, чтобы получить следующее число.

Пример последовательности нечетных чисел:

1. 1
2. 3
3. 5
4. 7
5. 9

Как можно заметить, каждое число в этой последовательности нечетное и больше предыдущего на 2.

Такую закономерность можно продолжать бесконечно, получая все больше и больше нечетных чисел.

Видео по теме:

Вопрос-ответ:

Что такое закономерность в математике?

Закономерность в математике — это последовательность чисел, событий или действий, которые повторяются с определенными правилами и порядком. Она может быть представлена в виде формулы, таблицы, графика или другого геометрического представления.

Как можно найти закономерность в математике?

Чтобы найти закономерность в математике, нужно проанализировать ряд чисел, событий или действий, определить их порядок и правила, по которым они повторяются. Можно использовать таблицы, графики или формулы для представления закономерности.

Какие примеры закономерности в математике есть для 3 класса?

Примеры закономерности в математике для 3 класса могут включать последовательности чисел, геометрические фигуры или повторяющиеся действия. Например, последовательность чисел 2, 4, 6, 8, 10 имеет закономерность увеличения на 2. Также, если взять геометрическую фигуру, такую как прямоугольник, и увеличивать его стороны в 2 раза каждый раз, мы получим закономерность увеличения площади в 4 раза.

Какие инструменты можно использовать для представления закономерности в математике?

Для представления закономерности в математике можно использовать различные инструменты, включая таблицы, графики, формулы и геометрические фигуры. Таблицы и графики могут помочь визуально представить последовательности чисел или событий. Формулы могут быть использованы для выражения закономерности в математической форме. Геометрические фигуры могут служить для иллюстрации закономерностей в пространстве.

Пример 4: Последовательность чисел Фибоначчи

Например, первые несколько чисел Фибоначчи выглядят следующим образом:

НомерЧисло Фибоначчи

1	0
2	1
3	1
4	2
5	3
6	5
7	8
8	13
9	21
10	34

Как видно из таблицы, каждое следующее число Фибоначчи равно сумме двух предыдущих чисел. Эта закономерность продолжается дальше, и можно вычислить любое число Фибоначчи, зная предыдущие два числа.

Последовательность чисел Фибоначчи имеет много интересных свойств и применений в математике, науке и даже искусстве.

Закономерность в математике для 3 класса: практическое применение

Закономерность в математике для 3 класса представляет собой упорядоченный ряд чисел или объектов, в котором можно выявить определенное правило. Практическое применение закономерности позволяет решать различные задачи и находить закономерности в реальных ситуациях.

Одним из практических примеров применения закономерности может быть расчет стоимости товаров. Например, если за одну единицу товара платят 10 рублей, то за 5 единиц товара нужно заплатить 50 рублей. Здесь можно применить закономерность умножения: стоимость товара равна количеству единиц, умноженному на цену одной единицы.

Другим примером может быть расчет времени, затраченного на выполнение задания. Если для выполнения одного задания требуется 5 минут, то для выполнения 4 заданий понадобится 20 минут. Здесь применяется закономерность умножения: время выполнения задания равно количеству заданий, умноженному на время выполнения одного задания.

Закономерность также может быть использована для нахождения недостающих элементов в ряде чисел или объектов. Например, если в ряде чисел 2, 4, 6, 8, 10 каждое следующее число увеличивается на 2, то следующее число будет равно 12. Здесь применяется закономерность сложения: каждое следующее число равно предыдущему числу, увеличенному на определенное число.

Практическое применение закономерности в математике помогает ученикам лучше понять математические операции, развивает логическое мышление и способствует решению задач различной сложности.