Что обозначает квадратные скобки в математике

Квадратные скобки в математике обозначают различные операции и концепции, такие как индексы, матрицы, векторы и множества. Узнайте, как использовать квадратные скобки в различных математических контекстах и как они влияют на обозначение и расчеты.

В математике квадратные скобки [] имеют особое значение и широко используются для обозначения различных математических объектов и операций. Они являются важным инструментом для представления данных и выражений в виде массивов, векторов, матриц, и многих других структур.

Одним из основных применений квадратных скобок является обозначение индексов, которые используются для доступа к элементам массивов. Например, если у нас есть массив a, то a[0] обозначает первый элемент этого массива. Индексы в квадратных скобках также используются для обращения к элементам векторов и матриц.

Квадратные скобки также используются для обозначения интервалов и диапазонов значений. Например, [a, b] обозначает интервал от a до b, включая оба конца. Также они могут использоваться для обозначения открытых и полуоткрытых интервалов, например, [a, b) обозначает интервал от a до b с включением a и исключением b.

Квадратные скобки также могут использоваться для обозначения множеств, областей определения функций, а также для обозначения антидифференциала. Они широко применяются в различных областях математики, включая алгебру, анализ, статистику, и дискретную математику.

Важно помнить, что значение квадратных скобок может зависеть от контекста и используемой нотации. Поэтому при работе с математическими выражениями и символами важно учитывать их семантику и особенности использования квадратных скобок в данном контексте.

Понятие квадратных скобок в математике

Квадратные скобки в математике обозначают различные концепции и операции, которые имеют особое значение в контексте математических выражений и уравнений.

Одним из наиболее распространенных использований квадратных скобок является обозначение интервалов. Когда в математике нужно указать непрерывный набор чисел, используются квадратные скобки. Например, интервал [1, 5] означает все числа, включая 1 и 5, находящиеся между ними.

Квадратные скобки также используются для обозначения матриц и векторов. В этом контексте квадратные скобки окружают элементы матрицы или вектора, разделенные запятыми или пробелами. Например, [1, 2, 3] обозначает вектор из трех элементов, а [[1, 2], [3, 4]] обозначает матрицу 2×2.

Еще одним важным применением квадратных скобок является обозначение индексов. В математических формулах квадратные скобки могут использоваться для указания индексов переменных или элементов. Например, x[1] обозначает первый элемент вектора x, а A[i, j] обозначает элемент матрицы A, находящийся в i-ой строке и j-ом столбце.

Квадратные скобки могут также использоваться для обозначения операций в математике. Например, [x] обозначает округление числа x до ближайшего целого, а [x]_p обозначает остаток от деления числа x на p.

Таким образом, квадратные скобки имеют разнообразные значения и применения в математике, и их использование зависит от контекста и задачи, которую необходимо решить.

Особенности использования квадратных скобок

Квадратные скобки в математике имеют несколько особенностей использования. Во-первых, они часто применяются для обозначения группировки элементов в математических выражениях. Например, в выражении (2 + 3) * 4 скобки обозначают группировку операций сложения и умножения.

Во-вторых, квадратные скобки могут использоваться для обозначения интервалов. Например, выражение [1, 5] обозначает интервал от 1 до 5 включительно. Такое использование квадратных скобок часто встречается в математическом анализе и теории множеств.

Кроме того, квадратные скобки могут использоваться для обозначения индексов. Например, если у нас есть последовательность чисел a_1, a_2, a_3, …, то a_n обозначает элемент с индексом n в этой последовательности.

Наконец, квадратные скобки могут быть использованы для обозначения матриц и векторов. Например, вектор [1, 2, 3] можно записать с помощью квадратных скобок. Также матрица может быть записана с помощью квадратных скобок, где каждая строка матрицы записывается внутри квадратных скобок, а элементы строки разделяются запятыми.

Применение квадратных скобок в алгебре

В алгебре квадратные скобки используются для обозначения нескольких важных понятий и операций.

Одним из основных применений квадратных скобок является обозначение матриц. Матрица — это упорядоченный набор чисел или выражений, расположенных в виде прямоугольной таблицы. Квадратные скобки используются для обрамления матрицы и подчеркивают ее специфическую структуру.

[ a11 a12 a13 ]

[ a21 a22 a23 ]

[ a31 a32 a33 ]

Квадратные скобки также используются для обозначения операций с векторами. Вектор — это упорядоченный набор чисел, которые могут быть представлены в виде столбца или строки. Квадратные скобки позволяют явно указать, что представленное выражение является вектором.

Примеры:

[ x1 ]

[ x2 ]

[ x3 ]

Кроме того, квадратные скобки используются для обозначения индексации элементов в математических выражениях и уравнениях. Индексация позволяет обращаться к конкретным элементам векторов или матриц.

Примеры:

x[1], x[2], x[3] — индексированные элементы вектора x

A[1,1], A[1,2], A[2,1] — индексированные элементы матрицы A

Таким образом, квадратные скобки являются важным синтаксическим элементом в алгебре, который позволяет обозначать и оперировать матрицами, векторами и их элементами.

Использование квадратных скобок в матричной алгебре

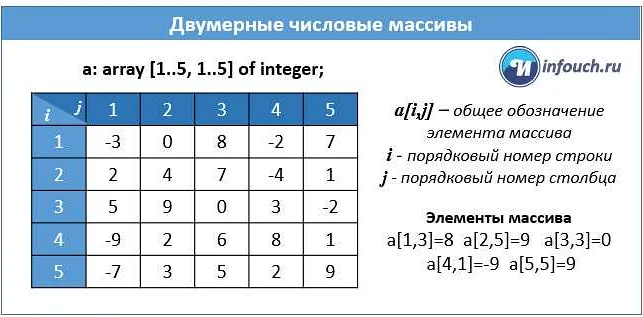
Квадратные скобки в матричной алгебре играют важную роль и используются для обозначения матриц и их элементов. Каждая матрица представляет собой прямоугольную таблицу, состоящую из элементов, которые располагаются в строках и столбцах. Квадратные скобки позволяют обращаться к отдельным элементам матрицы и выполнять операции с ними.

Обозначение элементов матрицы с помощью квадратных скобок происходит следующим образом: по горизонтали указывается номер строки, а по вертикали — номер столбца. Например, элемент матрицы А в первой строке и третьем столбце обозначается как А[1,3]. Таким образом, квадратные скобки позволяют однозначно идентифицировать и работать с каждым элементом матрицы.

Квадратные скобки также используются для задания размеров матрицы. Например, матрица А размером 2х3 обозначается как А[2,3]. Это означает, что матрица состоит из двух строк и трех столбцов. Такое обозначение позволяет удобно оперировать с матрицами различных размеров и выполнять операции над ними.

В матричной алгебре квадратные скобки также используются для обозначения операций над матрицами. Например, для сложения матриц А и В запись будет выглядеть как С = А + В. При этом квадратные скобки указывают на то, что выполняется операция над матрицами, а не над их элементами.

Таким образом, использование квадратных скобок в матричной алгебре позволяет однозначно обозначать элементы матрицы, задавать их размеры и выполнять операции над матрицами. Это делает матричную алгебру удобным и эффективным инструментом для работы с линейными системами уравнений и другими задачами, связанными с обработкой данных в виде матриц.

Роль квадратных скобок в теории вероятности

В теории вероятности квадратные скобки имеют особую роль и используются для обозначения вероятности события.

Обычно вероятность события обозначается как P(A), где A — само событие. Однако, в некоторых случаях, когда событие A может состоять из нескольких возможных исходов, квадратные скобки используются для указания множества всех возможных исходов.

Например, если A — событие «выпадение четного числа при броске кубика», то можно записать P(A) = 1/2. Но если A — событие «выпадение числа, кратного 3, при броске кубика», то можно записать P(A) = [1, 2, 3, 4, 5, 6]/6, где [1, 2, 3, 4, 5, 6] — множество всех возможных исходов.

Также квадратные скобки используются для обозначения условной вероятности. В этом случае, скобки располагаются после вероятности события, за которым следует символ |, и затем указывается условие.

Например, P(A|B) означает вероятность события A при условии события B. Если A — событие «выпадение четного числа при броске кубика» и B — событие «выпадение числа, кратного 3, при броске кубика», то можно записать P(A|B) = [2, 4, 6]/[1, 2, 3, 4, 5, 6], где [2, 4, 6] — множество исходов, соответствующих событию A, при условии события B, а [1, 2, 3, 4, 5, 6] — множество исходов, соответствующих событию B.

ПримерВероятность

Событие A	P(A) = [1, 2, 3, 4, 5, 6]/6
Событие B	P(B) = [1, 2, 3, 4, 5, 6]/6
Условная вероятность P(A|B)	P(A|B) = [2, 4, 6]/[1, 2, 3, 4, 5, 6]

Применение квадратных скобок в дифференциальном исчислении

В дифференциальном исчислении квадратные скобки используются для обозначения оператора «взятия производной». Если у нас есть функция, зависящая от одной или нескольких переменных, то производная этой функции по одной из переменных обозначается в следующем виде:

[f(x)]’ или [f(x1, x2, …, xn)]’

Здесь квадратные скобки вокруг функции указывают на то, что происходит операция дифференцирования.

Применение квадратных скобок позволяет ясно указать, какая именно функция дифференцируется. В случае, если функция зависит от нескольких переменных, то указание в квадратных скобках позволяет выбрать конкретную переменную по которой производится дифференцирование.

Например, если у нас есть функция f(x) = x^2, то ее производная по переменной x будет обозначаться следующим образом:

[f(x)]’ = [x^2]’ = 2x

Таким образом, квадратные скобки в дифференциальном исчислении играют важную роль, позволяя более точно указывать, какая функция дифференцируется и по какой переменной.

Использование квадратных скобок в функциональном анализе

Одним из основных применений квадратных скобок в функциональном анализе является обозначение нормы вектора или оператора. Норма вектора — это понятие, характеризующее «длину» вектора, а норма оператора — это понятие, характеризующее «размер» оператора. В обоих случаях квадратные скобки используются для обозначения нормы, например, $\|x\|$ для вектора $x$ и $\|A\|$ для оператора $A$.

Кроме того, квадратные скобки могут использоваться для обозначения пространства функций. Например, $L^p[a,b]$ обозначает пространство функций, определенных на отрезке $[a,b]$, для которых норма $p$-ой степени конечна. Здесь $p$ — это параметр, определяющий класс функций.

Квадратные скобки также могут использоваться для обозначения сопряженного оператора. Сопряженный оператор — это оператор, действующий в двойственном пространстве и обладающий определенными свойствами. Обозначение сопряженного оператора может выглядеть следующим образом: $A^*$.

В функциональном анализе квадратные скобки имеют еще множество других применений и используются для обозначения различных понятий и операций. Они являются важным инструментом для работы с функциями и операторами, и их правильное использование позволяет более точно и удобно формулировать математические выражения и утверждения.

Вопрос-ответ:

Зачем в математике используются квадратные скобки?

Квадратные скобки в математике используются для обозначения различных операций и свойств, таких как индексация, обозначение интервалов, матриц и многое другое.

Какие операции можно выполнять с квадратными скобками?

С помощью квадратных скобок можно выполнять операции индексации, а также обозначать интервалы, матрицы и некоторые другие математические объекты.

Какое значение имеют квадратные скобки в операции индексации?

В операции индексации квадратные скобки используются для обращения к отдельным элементам массива или другой структуры данных. Квадратные скобки содержат индекс элемента, к которому нужно обратиться.

Можно ли использовать квадратные скобки для обозначения интервалов?

Да, квадратные скобки часто используются для обозначения интервалов, включая начальное и конечное значение. Например, интервал [1, 5] включает все числа от 1 до 5 включительно.

Какие еще математические объекты могут обозначаться квадратными скобками?

Квадратные скобки могут использоваться для обозначения матриц, векторов, полей и других структур данных. Например, матрица A может быть обозначена как [A].

Значение квадратных скобок в теории множеств

В теории множеств квадратные скобки используются для обозначения различных операций и свойств множеств. Они позволяют указать границы и условия, которые должны выполняться при выполнении операций над множествами.

Одним из наиболее распространенных применений квадратных скобок является обозначение интервалов. Интервалы могут быть как конечными, так и бесконечными. Например, [a, b] обозначает замкнутый интервал, который включает все числа от a до b включительно. А (a, b) обозначает открытый интервал, который включает все числа между a и b, но исключает самые крайние значения a и b.

Квадратные скобки также используются для обозначения множества значений переменной. Например, [x] обозначает множество всех возможных значений переменной x. Это полезно при решении уравнений и систем уравнений, где требуется найти допустимые значения переменной.

Кроме того, квадратные скобки могут использоваться для обозначения операций над множествами. Например, [A ∪ B] обозначает объединение множеств A и B, то есть множество всех элементов, которые принадлежат хотя бы одному из множеств A или B. [A ∩ B] обозначает пересечение множеств A и B, то есть множество всех элементов, которые принадлежат одновременно и множеству A, и множеству B.

Важно отметить, что значения квадратных скобок могут зависеть от контекста и используемой математической нотации. Поэтому при изучении теории множеств необходимо учитывать конкретные правила и определения, установленные в данном контексте.

ОбозначениеОписание

[a, b]	Замкнутый интервал от a до b
(a, b)	Открытый интервал между a и b
[x]	Множество всех значений переменной x
[A ∪ B]	Объединение множеств A и B
[A ∩ B]	Пересечение множеств A и B

Видео по теме: