Что означает разряд в математике

Разряд в математике – это позиция цифры в числе, определяющая ее значение и величину. Узнайте, как работает система разрядов и как она помогает совершать арифметические операции.

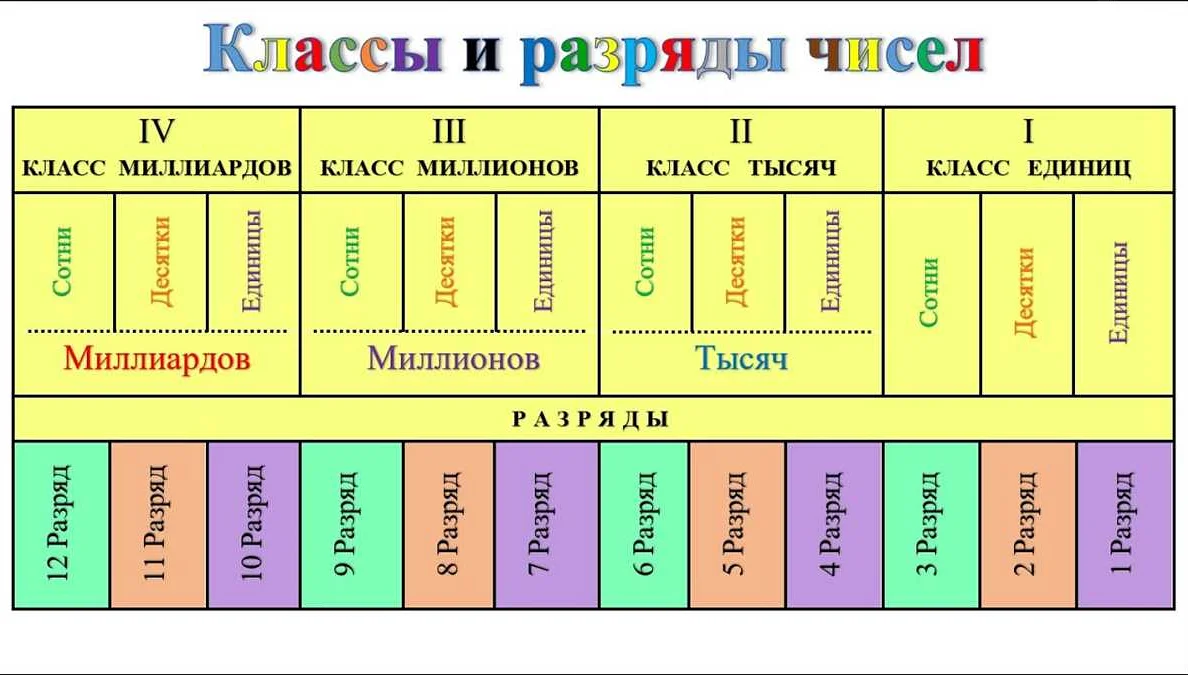
Разряд — это одна из основных составляющих числа, обозначающая его порядок и значение. В математике разряды используются для упорядочивания чисел и определения их места в числовой системе. Каждый разряд имеет свое значение, которое зависит от позиции числа в числовой записи.

В десятичной системе счисления разряды упорядочиваются справа налево. Первый разряд справа — это единицы, следующий — десятки, затем сотни и так далее. Каждый разряд умножается на соответствующую степень числа 10. Например, в числе 1234567 разряд единиц имеет значение 7, десятков — 6, сотен — 5 и т.д.

Разряды также применяются в других системах счисления, таких как двоичная, восьмеричная и шестнадцатеричная. В этих системах разряды упорядочиваются аналогично, только каждый разряд умножается на соответствующую степень основания системы счисления.

Знание понятия разряда и его значения позволяет легче понимать и работать с числами. Например, при сложении или вычитании чисел, необходимо учитывать разряды и правильно расставлять знаки. Также, знание разрядов позволяет легко определять кратность числа или количество его цифр.

В заключение, разряды играют важную роль в математике, помогая нам понимать и работать с числами. Знание разрядов позволяет нам упорядочивать числа, определять их значение и правильно выполнять арифметические операции. Поэтому понимание значения разрядов в математике является неотъемлемой частью нашего математического образования.

Разряд числа: определение и особенности

В математике, число может быть представлено в разрядной системе счисления, где оно разбивается на разряды. Каждый разряд в числе имеет свою позицию и значение, которое зависит от основания системы счисления.

Основание системы счисления определяет количество различных символов, которые могут быть использованы для представления чисел. В десятичной системе счисления основание равно 10, и используются цифры от 0 до 9. В двоичной системе счисления основание равно 2, и используются только цифры 0 и 1.

Каждый разряд числа имеет свою весовую степень, которая определяет его значимость. Например, в десятичной системе счисления разряды имеют следующие весовые степени: 10^0 (единицы), 10^1 (десятки), 10^2 (сотни), 10^3 (тысячи) и так далее.

Значение разряда в числе определяется умножением его цифры на соответствующую весовую степень. Например, в числе 532, значение разряда «2» равно 2 * 10^0 = 2, значение разряда «3» равно 3 * 10^1 = 30, и значение разряда «5» равно 5 * 10^2 = 500.

Разряды числа также могут быть отрицательными. В этом случае их весовая степень будет отрицательной. Например, в числе 0.007, значение разряда «7» равно 7 * 10^(-3) = 0.007.

Разряды числа позволяют представлять большие числа в более компактной форме и упрощают выполнение арифметических операций. Они также играют важную роль при работе с числовыми системами, такими как двоичная, восьмеричная и шестнадцатеричная.

Значение разряда в десятичной системе счисления

Разряд в десятичной системе счисления определяет вес числа и позволяет представить любое число с помощью десяти разрядов. В десятичной системе счисления используются цифры от 0 до 9.

Каждый разряд имеет определенное значение, которое зависит от его позиции в числе. Например, число 1234 в десятичной системе состоит из четырех разрядов: тысяч, сотен, десятков и единиц. Значение каждого разряда определяется следующим образом:

• Тысячный разряд имеет значение 1000. В числе 1234, цифра 1 стоит на тысячном разряде, поэтому ее значение равно 1000.
• Сотый разряд имеет значение 100. В числе 1234, цифра 2 стоит на сотом разряде, поэтому ее значение равно 200.
• Десятый разряд имеет значение 10. В числе 1234, цифра 3 стоит на десятом разряде, поэтому ее значение равно 30.
• Единичный разряд имеет значение 1. В числе 1234, цифра 4 стоит на единичном разряде, поэтому ее значение равно 4.

Таким образом, число 1234 в десятичной системе счисления можно представить как сумму произведений каждого разряда на его значение: 1 * 1000 + 2 * 100 + 3 * 10 + 4 * 1 = 1234.

Знание значения разрядов в десятичной системе счисления позволяет проводить различные операции с числами, такие как сложение, вычитание, умножение и деление.

Примеры разряда в десятичной системе счисления

Разряды в десятичной системе счисления представляют собой позиции цифр в числе. Каждый разряд имеет своё значение, которое зависит от позиции цифры в числе. В десятичной системе счисления используются следующие разряды:

• Единицы — самый младший разряд, значение которого не меняется в зависимости от позиции цифры.
• Десятки — разряд, значение которого увеличивается в 10 раз по сравнению с единицами.
• Сотни — разряд, значение которого увеличивается в 100 раз по сравнению с единицами.
• Тысячи — разряд, значение которого увеличивается в 1000 раз по сравнению с единицами.
• Миллионы — разряд, значение которого увеличивается в 1 000 000 раз по сравнению с единицами.

Например, число 1234567 имеет следующую разрядную структуру:

МиллионыСотни тысячДесятки тысячТысячиСотниДесяткиЕдиницы

1

2

3

4

5

6

7

Таким образом, значение каждого разряда в числе 1234567 определяется его позицией и влияет на общее значение числа.

Значение разряда в двоичной системе счисления

Разряды в двоичной системе счисления увеличиваются справа налево. Каждый разряд имеет вес, который определяет его значение. Начиная с самого правого разряда, вес каждого следующего разряда увеличивается вдвое.

Например, в двоичном числе 1101 разряды имеют следующие веса:

РазрядВес

1	8
1	4
0	2
1	1

Чтобы вычислить десятичное значение двоичного числа, нужно умножить каждую цифру числа на ее вес и сложить полученные значения. Поэтому число 1101 в двоичной системе счисления равно 8 + 4 + 0 + 1 = 13 в десятичной системе счисления.

Примеры разряда в двоичной системе счисления

Рассмотрим число 1101, записанное в двоичной системе счисления. В этом числе есть следующие позиции разрядов:

1-й разряд: Значение — 1, Вес — 23 = 8

2-й разряд: Значение — 1, Вес — 22 = 4

3-й разряд: Значение — 0, Вес — 21 = 2

4-й разряд: Значение — 1, Вес — 20 = 1

Сложив произведения значений и весов разрядов, получим итоговое значение числа:

11012 = 8 + 4 + 0 + 1 = 13

Таким образом, число 1101 в двоичной системе счисления равно числу 13 в десятичной системе счисления.

Значение разряда в восьмеричной системе счисления

Значение разряда в восьмеричной системе счисления определяется как произведение цифры на основание возведенное в степень позиции разряда.

Например, в числе 3518:

• 1 — это цифра разряда единиц, она умножается на 80 (1), что даёт 1.
• 5 — это цифра разряда восьмерок, она умножается на 81 (8), что даёт 40.
• 3 — это цифра разряда шестнадцатерок, она умножается на 82 (64), что даёт 192.

Таким образом, число 3518 в десятичной системе счисления равно 233.

Значение разряда в восьмеричной системе счисления имеет важное значение при выполнении различных операций, таких как сложение, вычитание, умножение и деление в этой системе счисления.

Примеры разряда в восьмеричной системе счисления

Рассмотрим несколько примеров разряда в восьмеричной системе счисления:

РазрядЗначениеПример

Единицы	8^0 = 1	168 = 1 * 8^0 = 1
Восьмерки	8^1 = 8	248 = 2 * 8^1 + 4 * 8^0 = 16 + 4 = 20
Шестидесятерки	8^2 = 64	1748 = 1 * 8^2 + 7 * 8^1 + 4 * 8^0 = 64 + 56 + 4 = 124

Как видно из примеров, значение каждого разряда в восьмеричной системе счисления зависит от его позиции. Зная значения разрядов, можно легко переводить числа из одной системы счисления в другую и выполнять различные арифметические операции.

Значение разряда в шестнадцатеричной системе счисления

В шестнадцатеричной системе счисления каждая позиция числа имеет свое значение разряда, аналогично десятичной системе. Отличие заключается в том, что каждый разряд имеет вес, равный степени 16. Первый разряд считается самым младшим разрядом и имеет вес 16^0, второй разряд — вес 16^1, третий разряд — вес 16^2 и так далее.

Например, число 3A7 в шестнадцатеричной системе можно разложить на разряды и их значения:

• Третий разряд (A) имеет вес 16^2 = 256
• Второй разряд (7) имеет вес 16^1 = 16
• Первый разряд (3) имеет вес 16^0 = 1

Таким образом, число 3A7 в шестнадцатеричной системе счисления равно 3 * 256 + 10 * 16 + 7 * 1 = 935 в десятичной системе счисления.

Шестнадцатеричная система счисления широко применяется в программировании, особенно при работе с памятью компьютера и представлении цветов. Знание значения разрядов в шестнадцатеричной системе счисления является важным для понимания и работы с числами в этой системе.

Видео по теме:

Что такое разряд в математике?

Разряд в математике — это позиция числа в его записи. Каждая позиция представляет определенную степень числа 10. Например, в числе 123, разряд единиц представляет число 3, разряд десятков — число 2, а разряд сотен — число 1.

Каково значение разрядов в десятичной системе счисления?

В десятичной системе счисления разряды имеют следующие значения: разряд единиц — 10 в степени 0, разряд десятков — 10 в степени 1, разряд сотен — 10 в степени 2, разряд тысяч — 10 в степени 3, и так далее.

Как можно использовать понятие разряда в математике для решения задач?

Понятие разряда в математике позволяет проводить операции с числами, анализировать их свойства и делать выводы. Например, для сложения или умножения больших чисел, выравнивают их разряды и выполняют операции по каждому разряду отдельно. Также, знание разрядов помогает определить значимость каждой цифры в числе.