Что значит стрелочка в математике

Стрелочка в математике — это символ, который используется для обозначения различных математических операций, направлений или отношений. Узнайте, какие значения и назначения могут иметь стрелочки в математике и как они могут помочь в понимании математических концепций.

Стрелочка в математике является важным символом, который используется для обозначения различных математических понятий и операций. Она помогает нам понять связь между числами, выражениями и функциями.

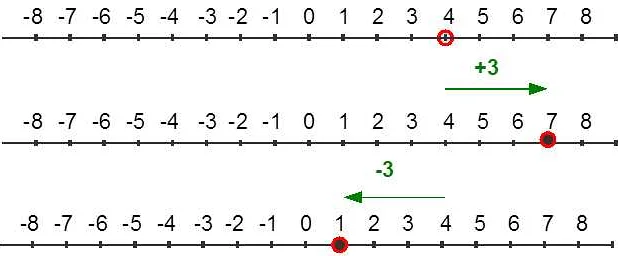
Одно из самых распространенных значений стрелочки в математике — это указание направления или отношения между двумя элементами. Например, стрелочка может обозначать направление движения или отношение порядка чисел на числовой прямой.

Например, если у нас есть числа 2 и 6, мы можем записать их с помощью стрелочки следующим образом: 2 → 6. В этом случае стрелочка указывает на то, что число 2 находится перед числом 6 на числовой прямой.

Стрелочка также может использоваться для обозначения функций. В этом случае она указывает на то, что значение одной величины зависит от значения другой. Например, если у нас есть функция f(x) = 2x, мы можем записать это с помощью стрелочки следующим образом: f(x) → 2x. В этом случае стрелочка указывает на то, что значение функции f(x) зависит от значения переменной x и равно удвоенному значению x.

Таким образом, стрелочка в математике играет важную роль в обозначении отношений, направлений и функций. Она помогает нам лучше понять математические концепции и связи между различными элементами.

Стрелочка в математике: обозначение направления

Стрелочка в математике используется для обозначения направления или отношения между двумя элементами. Она может быть использована в различных контекстах и иметь различные значения.

Векторные стрелки:

Векторы в математике часто обозначаются с помощью стрелки над буквой, например, AB →. Векторная стрелка указывает на направление и величину вектора. Направление указывается от начала до конца стрелки, а величина вектора определяется длиной стрелки.

Стрелка в уравнениях:

В уравнениях стрелка может использоваться для обозначения отношения между переменными или операций. Например, a → b означает, что переменная a зависит от переменной b или что операция a выполняется после операции b.

Стрелочка в геометрии:

В геометрии стрелка может использоваться для обозначения направления движения или вектора перемещения. Например, AB → может означать движение от точки A до точки B или вектор перемещения от точки A до точки B.

Все эти примеры показывают, что стрелочка в математике имеет важное значение и помогает нам лучше понять и описать отношения и направления в различных математических контекстах.

Стрелочка в математике: обозначение вектора

В математике стрелочка над символом часто используется для обозначения вектора. Вектор представляет собой величину, которая имеет как величину, так и направление. Стрелочка указывает на направление вектора и отличает его от обычной скалярной величины.

Обозначение вектора с помощью стрелочки обычно записывается над символом. Например, вектор a может быть записан как ←a→ или ↑a↓. Стрелочка может быть как одиночной, так и двойной, в зависимости от предпочтений автора или стандартов, используемых в конкретной области математики.

Использование стрелочки в обозначении вектора позволяет наглядно представить его направление. Например, вектор a может быть направлен вправо или влево, вверх или вниз, а стрелочка указывает на это направление.

Примеры использования стрелочки в обозначении вектора:

ВекторОбозначение

Вектор a	←a→
Вектор b	↑b↓
Вектор c	→c←

Использование стрелочки в обозначении вектора является стандартным и широко применяется в различных областях математики, физики и других наук. Это позволяет более точно и наглядно описывать векторные величины и их свойства.

Стрелочка в математике: обозначение функции

Стрелочка в математике используется для обозначения функции. Функция определяет соответствие между элементами двух множеств, называемых областью определения и областью значений.

Обозначение функции с помощью стрелочки имеет следующий вид:

Область определенияСтрелочкаОбласть значений

x

→

f(x)

Где x — переменная или аргумент функции, → — стрелочка, обозначающая отображение, а f(x) — значение функции при заданном аргументе.

Например, функция f(x) = 2x + 1 можно записать с использованием стрелочки:

Область определенияСтрелочкаОбласть значений

x

→

2x + 1

Такое обозначение позволяет ясно указать зависимость между переменной x и значением функции.

Стрелочка в математике: обозначение пропорциональности

Пропорциональность — это соотношение, при котором две величины меняются в одинаковой пропорции. Стрелочка используется для обозначения этого соотношения.

Например, если мы имеем две величины, A и B, и они пропорциональны друг другу, то это можно записать с помощью стрелочки следующим образом: A ∝ B. Выражение A ∝ B означает, что A и B связаны между собой пропорциональным соотношением.

Для более точного обозначения пропорциональности можно использовать знак равенства с двумя параллельными вертикальными чертами. Такое обозначение выглядит следующим образом: A ∝ B. Выражение A ∝ B также означает пропорциональность между A и B.

Пропорциональность широко используется в различных областях математики и науки, таких как физика, экономика и статистика. Знание и понимание обозначения пропорциональности с помощью стрелочки позволяет более точно и ясно выражать соотношения между величинами.

Стрелочка в математике: обозначение отношения

Одним из основных применений стрелочки в математике является обозначение отношения между двумя объектами. Например, стрелочка может указывать на связь между двумя числами, множествами или другими математическими объектами. Эта связь может иметь различные характеристики, такие как равенство, неравенство, принадлежность, включение и другие.

Например, стрелочка «=» обозначает отношение равенства. Если написать «2 + 2 = 4», это означает, что сумма двух чисел 2 и 2 равна числу 4. Стрелочка «≠» обозначает отношение неравенства. Например, «3 ≠ 5» означает, что число 3 не равно числу 5.

Стрелочка также может использоваться для обозначения отношения принадлежности между элементами множеств. Например, «3 ∈ {1, 2, 3, 4}» означает, что число 3 принадлежит множеству {1, 2, 3, 4}. Стрелочка «⊂» обозначает отношение включения между множествами. Например, «{1, 2} ⊂ {1, 2, 3}» означает, что множество {1, 2} включено в множество {1, 2, 3}, но не равно ему.

Таким образом, стрелочка в математике играет важную роль в обозначении различных отношений между математическими объектами. Правильное понимание и использование стрелочки позволяет математикам точно и ясно выражать эти отношения.

Стрелочка в математике: обозначение преобразования

В математике стрелочка или «стрелка» часто используется для обозначения преобразования или отображения между математическими объектами.

Преобразование обычно представляет собой связь между двумя множествами, где каждому элементу из одного множества соответствует элемент из другого множества. Стрелочка используется для указания этой связи.

Например, если у нас есть множество чисел {1, 2, 3} и мы хотим умножить каждое число на 2, мы можем использовать стрелочку для обозначения этого преобразования:

Множество чисел {1, 2, 3} → Множество чисел {2, 4, 6}

В этом случае стрелочка указывает на преобразование, которое умножает каждое число из исходного множества на 2 и дает новое множество чисел.

Стрелочка также может использоваться для обозначения преобразования между переменными или функциями. Например, если у нас есть функция f(x) = x^2, мы можем использовать стрелочку для обозначения преобразования этой функции:

f(x) = x^2 → f(2) = 4

Здесь стрелочка указывает на то, что мы применяем функцию f к переменной x и получаем новое значение f(x).

Таким образом, стрелочка в математике играет важную роль в обозначении преобразований и связей между математическими объектами.

Стрелочка в математике: обозначение принадлежности

В математике стрелочка используется для обозначения принадлежности элемента к множеству. Обычно это обозначается символом ∈, который выглядит как стрелочка направленная влево.

Например, если у нас есть множество натуральных чисел N = {1, 2, 3, 4, …}, и мы хотим указать, что число 2 принадлежит этому множеству, мы можем записать это следующим образом:

2 ∈ N

Это читается как «2 принадлежит множеству натуральных чисел». Символ ∈ можно также заменить словом «принадлежит» или символом «∈». В обозначениях множеств можно использовать разные символы, но стрелочка является одним из наиболее распространенных и удобных обозначений.

Стрелочка также может использоваться вместе с кванторами для обозначения принадлежности элемента к множеству в пределах некоторого утверждения. Например, если у нас есть множество натуральных чисел N = {1, 2, 3, 4, …} и мы хотим указать, что каждое число этого множества является четным, мы можем записать это следующим образом:

∀n (n ∈ N → n % 2 = 0)

Это читается как «для любого числа n, принадлежащего множеству натуральных чисел, если n делится на 2 без остатка, то n является четным». Здесь стрелочка указывает на связь между элементом и утверждением.

Таким образом, стрелочка в математике играет важную роль в обозначении принадлежности элемента к множеству и указывает на связь между элементами и утверждениями.

Стрелочка в математике: обозначение изоморфизма

Изоморфизм — это отношение между двумя алгебраическими структурами, которое сохраняет их структурные свойства. Изоморфные структуры имеют одинаковые свойства и можно считать их эквивалентными.

Обозначение изоморфизма обычно выглядит как стрелочка с двумя вертикальными чертами под ней:

≈

Такая стрелочка обычно рисуется между двумя математическими объектами, которые являются изоморфными друг другу. Например, если мы имеем два графа, которые изоморфны друг другу, мы можем обозначить это следующим образом:

G ≈ H

Здесь G и H — это два графа, а стрелочка с двумя вертикальными чертами обозначает, что они изоморфны.

Изоморфизм в математике играет важную роль при изучении различных структур и их свойств. Он позволяет установить соответствие между объектами, имеющими общие характеристики, и проводить аналогии и выводы относительно свойств этих объектов.

Вопрос-ответ:

Зачем нужна стрелочка в математике?

Стрелочка в математике используется для обозначения различных понятий, например, направления движения, равенства или неравенства, функциональной зависимости и т.д. Она является важным инструментом для формулировки математических утверждений и выражения математических отношений.

Какие примеры использования стрелочки в математике?

Примеры использования стрелочки в математике многообразны. Например, в уравнении x + 2 = 5 стрелочка указывает на равенство: x = 3. В неравенстве 3x > 12 стрелочка указывает на неравенство «больше». Также стрелочка используется для обозначения функций, например, f(x) = x^2, где стрелочка указывает на зависимость переменной x от функции f.

Как правильно читать стрелочку в математике?

Чтение стрелочки в математике зависит от контекста. Например, стрелочку «→» можно прочитать как «выражение», «из», «в», «превращается в» и т.д. Например, если дано уравнение x + 2 = 5, то стрелочку можно прочитать как «x плюс 2 равно 5» или «x равно 5 минус 2». Важно учитывать смысл и контекст математического выражения.

Каково значение стрелочки «⇒» в математике?

Стрелочка «⇒» в математике обозначает импликацию или следствие. Она используется для выражения логической связи «если… то…» или «из… следует…». Например, выражение «если x > 0, то x^2 > 0» можно записать как «x > 0 ⇒ x^2 > 0». Это означает, что если x больше нуля, то x в квадрате также будет больше нуля.

Можете привести пример использования стрелочки «→» для обозначения функции?

Конечно! Для обозначения функции стрелочка «→» используется следующим образом. Например, пусть дана функция f(x) = 2x + 1. Здесь стрелочка указывает на зависимость переменной x от функции f. Это означает, что значение функции f(x) равно удвоенному значению переменной x плюс 1. Таким образом, если мы подставим значение x, то можем вычислить значение функции.

Зачем нужна стрелочка в математике?

Стрелочка в математике используется для обозначения различных операций и отношений между числами или объектами. Она помогает нам понять, какие действия мы выполняем с числами и какие связи существуют между ними.

Видео по теме: