Что такое числовая прямая в математике

Числовая прямая — графическое представление всех действительных чисел на прямой линии. Она помогает визуализировать и упорядочить числа, а также выполнять операции сложения и вычитания. Узнайте, как использовать числовую прямую для решения математических задач и понимания числовых отношений.

Числовая прямая является основным инструментом в математике, используемым для представления и изучения чисел и их взаимного расположения. Она представляет собой прямую линию, на которой каждой точке соответствует определенное число. Числовая прямая позволяет наглядно представить числовые значения и осуществлять операции с ними.

Основные понятия, связанные с числовой прямой, включают точки, отрезки и направление. Точки на числовой прямой представляют собой соответствующие числу значения. Отрезки на числовой прямой обозначают разницу между двумя числами и могут быть положительными или отрицательными. Направление на числовой прямой указывает, как движутся числа по отрезкам: вправо или влево.

Пример использования числовой прямой может быть в задачах на определение расстояния между двумя точками, нахождение среднего значения или решение уравнений. Например, если на числовой прямой даны точки A (-3) и B (5), то расстояние между ними можно найти как сумму абсолютных значений отрезков, то есть |(-3)| + |5| = 3 + 5 = 8. Также числовая прямая позволяет наглядно представить, как изменяется значение функции в зависимости от аргумента и выявить ее особые точки и интервалы монотонности.

Определение числовой прямой в математике

На числовой прямой имеются два направления: вправо и влево. Центральная точка называется началом, обозначается нулем (0) и разделяет прямую на две полуоси. Положительные числа располагаются справа от нуля, а отрицательные — слева.

Числовая прямая позволяет легко визуализировать и сравнивать числа. Большие числа находятся дальше от нуля, а маленькие — ближе. Расстояние между двумя точками на числовой прямой соответствует разности чисел, которым они соответствуют.

Числовая прямая широко используется в математике и других науках для изучения различных математических концепций, таких как алгебра, геометрия, анализ и теория вероятности. Она также находит применение в физике, экономике и других областях, где числа играют важную роль.

Видео по теме:

Основные понятия числовой прямой

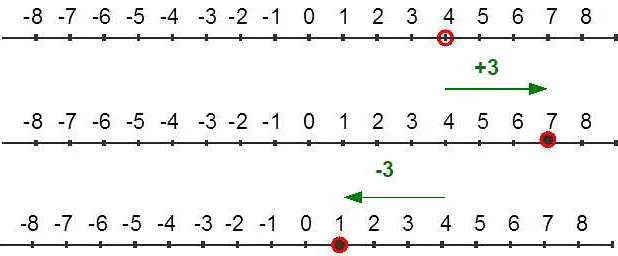
На числовой прямой можно отметить точки, которые соответствуют конкретным числам. Расстояние между двумя точками на числовой прямой называется абсолютной величиной разности этих чисел.

Числовая прямая также имеет направление. Отрицательные числа располагаются слева от нуля и увеличиваются по мере движения влево, а положительные числа находятся справа от нуля и увеличиваются по мере движения вправо.

Числовая прямая используется для отображения различных математических концепций, таких как алгебраические операции, решение уравнений, графики функций и многое другое. Она является важным инструментом для визуализации и работы с числами.

Шкала числовой прямой

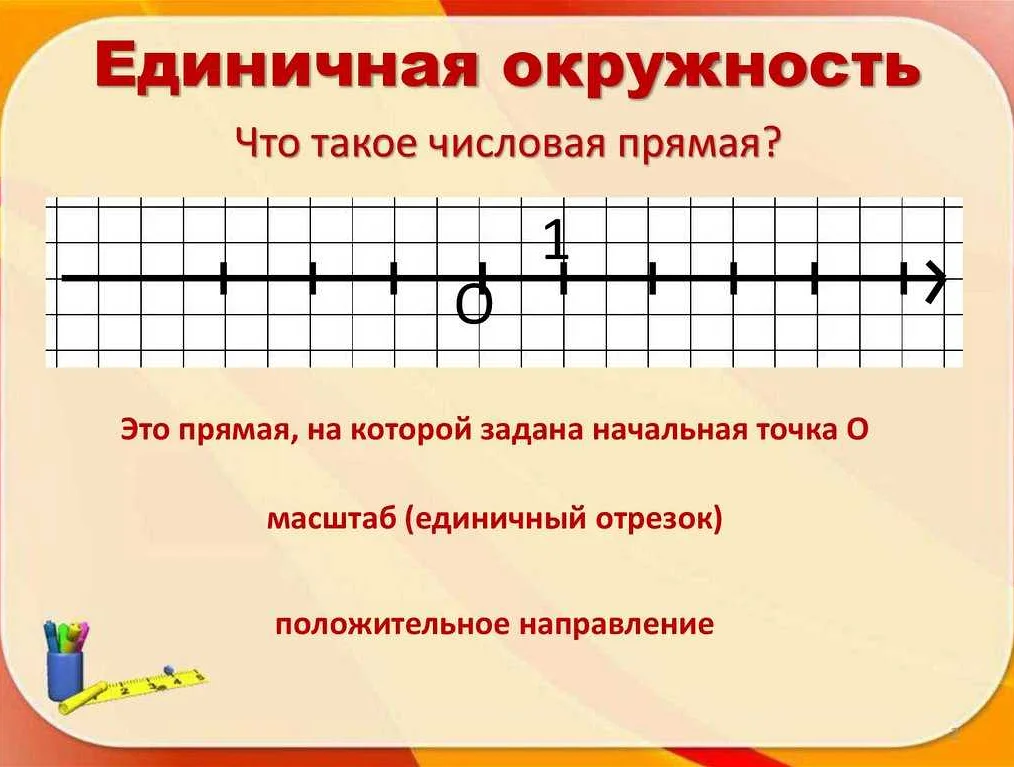
Шкала числовой прямой представляет собой горизонтальную линию, на которой отмечены числа. Числа на шкале могут быть расположены в порядке возрастания или убывания, и между ними должны быть одинаковые промежутки.

Шкала числовой прямой используется для визуализации числовых данных и отображения их относительного положения на числовой оси. Каждая точка на числовой прямой соответствует определенному числу, и можно сравнивать числа, находящиеся с разных сторон от нуля.

На числовой прямой можно отмечать не только целые числа, но и дробные или отрицательные числа. Также можно использовать шкалу для отображения диапазона значений, например, от -10 до 10.

ЧислоТочка на числовой прямой

0	•
1	•
2	•
3	•

На примере таблицы видно, что каждому числу соответствует точка на числовой прямой. Точка может быть отмечена с помощью специального символа или через отрезок, на котором находится данное число.

Отрицательные числа на числовой прямой

Одним из важных понятий на числовой прямой являются отрицательные числа. Отрицательные числа располагаются слева от нуля на числовой прямой и представляют собой числа, меньшие нуля.

При отображении отрицательных чисел на числовой прямой, каждое число обозначается точкой, которая находится слева от нуля, а расстояние от этой точки до нуля определяет величину числа. Чем дальше число находится от нуля, тем больше его величина.

Например, число -3 будет обозначено точкой, которая находится на расстоянии трех единиц слева от нуля. А число -1/2 будет обозначено точкой, которая находится на полпути между нулем и -1.

Отрицательное числоТочка на числовой прямой

-3	—
-2	—
-1	—
-1/2	—
-1/4	—

Отрицательные числа на числовой прямой позволяют нам работать с такими понятиями, как отрицательные значения, задолженность, убытки и многое другое. Они также играют важную роль в математике, физике, экономике и других науках.

Положительные числа на числовой прямой

Положительные числа на числовой прямой располагаются справа от нуля. Ноль является центром числовой прямой и разделяет ее на две части: положительные числа и отрицательные числа.

Например, число 3 располагается справа от нуля на числовой прямой. Это означает, что оно больше нуля. Аналогично, любое число, которое больше нуля, будет положительным числом и будет располагаться справа от нуля.

Положительные числа на числовой прямой имеют следующие свойства:

• Они увеличиваются по мере движения вправо;
• Они могут быть представлены в виде отрезков на числовой прямой;
• Чем дальше вправо на числовой прямой находится положительное число, тем больше оно.

Понимание расположения положительных чисел на числовой прямой позволяет легче работать с числами и выполнять различные математические операции, такие как сложение, вычитание, умножение и деление.

Ноль на числовой прямой

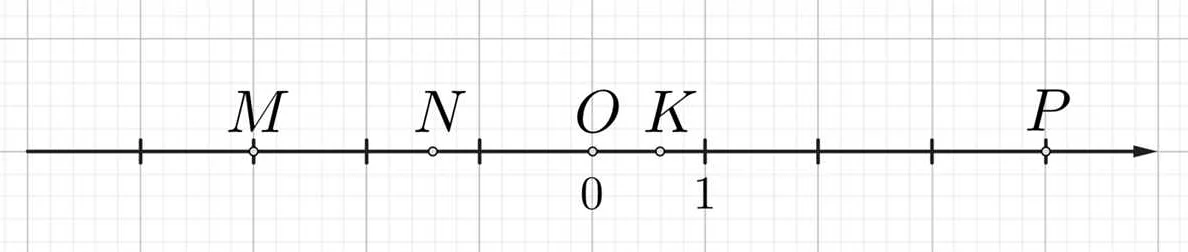
Ноль является уникальным числом, так как при умножении на ноль любое число будет равно нулю. Это свойство нуля называется нулевым свойством. Также, при делении нуля на любое число, результатом будет ноль, за исключением деления нуля на ноль, которое не имеет определенного значения.

Ноль также играет важную роль в математических операциях. Например, при сложении нуля с любым числом, результат будет равен этому числу. То есть, a + 0 = a, где a — произвольное число. А при вычитании нуля из любого числа, результат также останется неизменным: a — 0 = a.

Ноль также является основой для определения отрицательных чисел. Число, которое располагается слева от нуля на числовой прямой, считается отрицательным. Например, -1, -2, -3 и так далее. А число, которое располагается справа от нуля, считается положительным. Например, 1, 2, 3 и т.д.

Таким образом, ноль является важным понятием на числовой прямой и играет важную роль в математике.

Расположение чисел на числовой прямой

Числа на числовой прямой располагаются по порядку. Чем дальше число от нуля, тем больше оно. Ноль находится в центре числовой прямой и является точкой отсчета для положительных и отрицательных чисел.

Отрицательные числа располагаются слева от нуля на числовой прямой. Чем дальше число от нуля влево, тем меньше оно. Например, -3 находится слева от -2 и -1.

Положительные числа располагаются справа от нуля на числовой прямой. Чем дальше число от нуля вправо, тем больше оно. Например, 1 находится справа от 0, а 3 — справа от 2 и 1.

Числа на числовой прямой можно представить в виде таблицы, где в первом столбце указываются числа, а во втором столбце — их расположение на числовой прямой:

ЧислоРасположение на числовой прямой

-3	слева от -2 и -1
-2	слева от -1
-1	слева от 0
0	центр числовой прямой
1	справа от 0
2	справа от 1
3	справа от 2 и 1

Таким образом, расположение чисел на числовой прямой позволяет наглядно представить и сравнить их величину, а также оперировать с ними в математических выражениях.

Примеры использования числовой прямой в математике

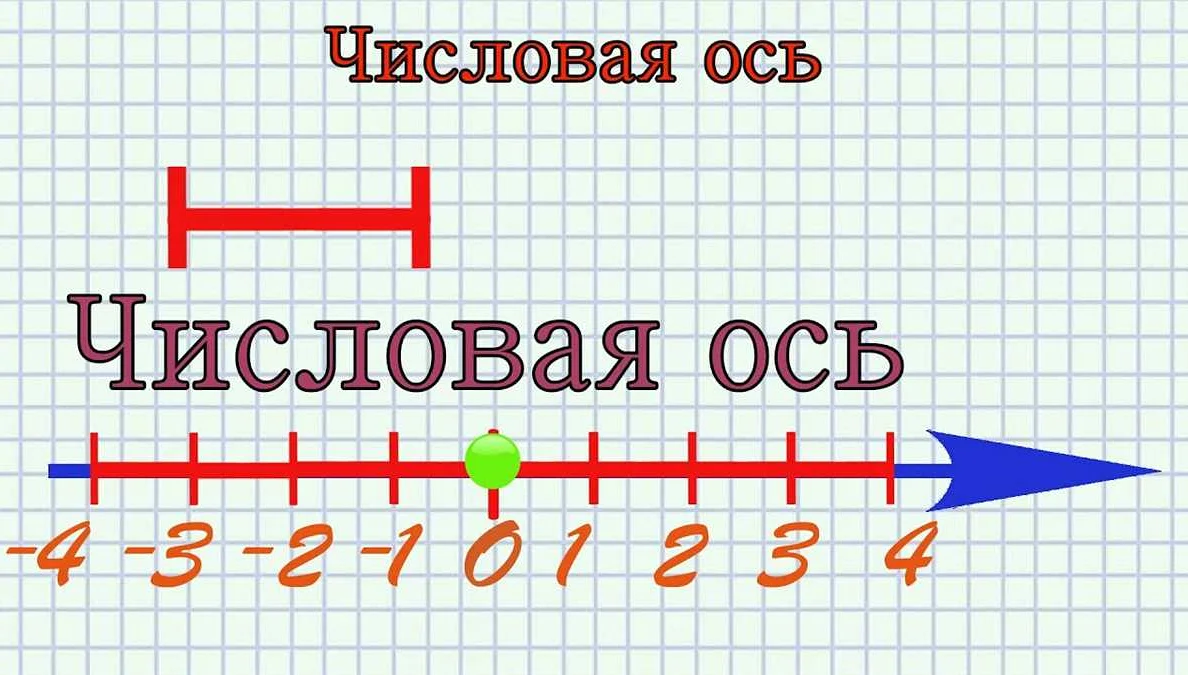
Вот несколько примеров использования числовой прямой:

• Представление чисел: Числовая прямая позволяет наглядно представить числа и их отношения. На числовой прямой можно отметить точки, соответствующие различным числам, и сравнивать их положение относительно друг друга.
• Решение уравнений и неравенств: Числовая прямая помогает в решении уравнений и неравенств. При решении уравнений можно представить уравнение в виде графической задачи и определить точки пересечения графика с осью. При решении неравенств можно использовать числовую прямую для представления интервалов, удовлетворяющих неравенству.
• Анализ функций: Числовая прямая используется для анализа функций. График функции может быть построен на числовой прямой, что позволяет визуализировать поведение функции и определить ее свойства, такие как возрастание, убывание, экстремумы и точки перегиба.
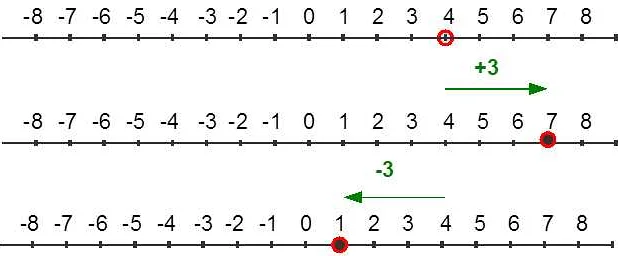
• Изучение арифметических операций: Числовая прямая применяется при изучении арифметических операций, таких как сложение, вычитание, умножение и деление. Она помогает визуализировать и понять действия с числами, например, показывает, что сложение двух положительных чисел приводит к увеличению значения.
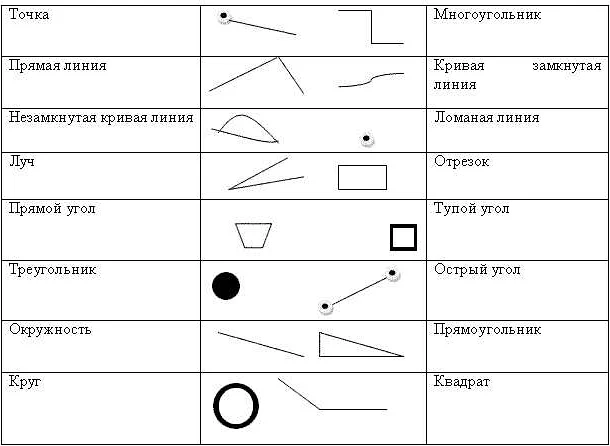
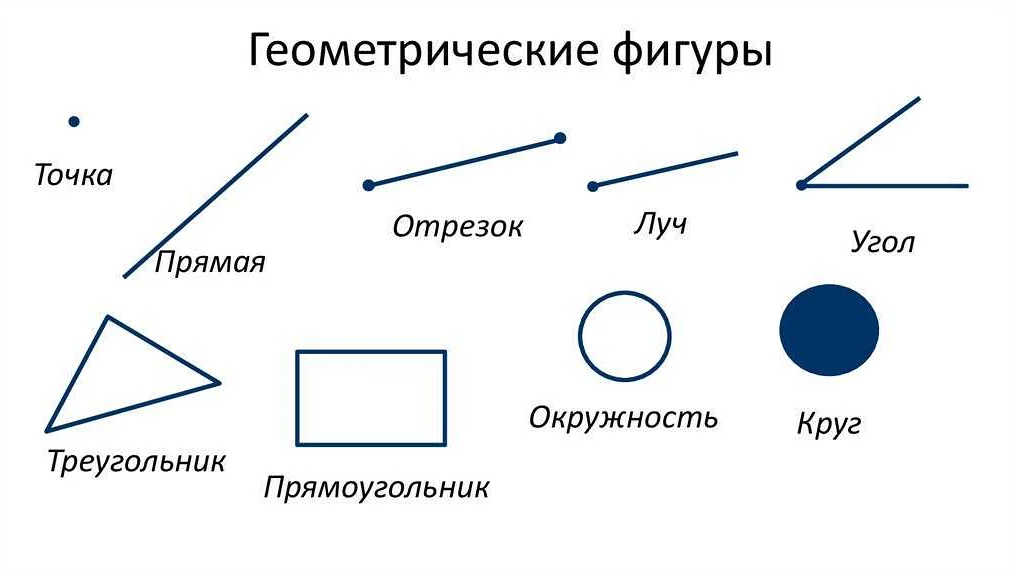
• Геометрические построения: Числовая прямая используется в геометрии для построения различных фигур и отрезков. Она позволяет определить точки на прямой и измерить их относительное расположение.

Это лишь некоторые примеры использования числовой прямой в математике. Она широко применяется в различных областях и играет важную роль в понимании и анализе числовых данных.

Вопрос-ответ:

Зачем нужна числовая прямая?

Числовая прямая является удобным графическим инструментом для визуализации чисел и их отношений. Она позволяет представить все числа, отрицательные и положительные, а также нуль, в виде точек на оси. Также числовая прямая используется для изучения алгебры, геометрии и различных математических операций.

Какие основные понятия связаны с числовой прямой?

Основные понятия, связанные с числовой прямой, включают точки, отрезки, положительные и отрицательные числа, ноль, направление движения и единицу измерения. Точки представляют собой значения чисел на числовой прямой, отрезки — интервалы между двумя точками. Положительные числа располагаются справа от нуля, а отрицательные — слева. Ноль находится в центре числовой прямой. Направление движения указывает, куда движется значение числа при увеличении или уменьшении. Единица измерения используется для обозначения размера интервалов на числовой прямой.

Как применяется числовая прямая в алгебре?

Числовая прямая в алгебре используется для решения уравнений и неравенств. Она помогает представить значения переменных и их отношения графически, что облегчает анализ их свойств. Например, графическое представление можно использовать для определения решений уравнений или неравенств, а также для нахождения интервалов, в которых значения переменных удовлетворяют условиям задачи.

Как использовать числовую прямую для сравнения чисел?

Для сравнения чисел на числовой прямой нужно найти их соответствующие точки и определить их расположение относительно друг друга. Если точка, соответствующая одному числу, находится правее точки другого числа, значит, первое число больше. Если точка находится левее, то оно меньше. Таким образом, числовая прямая позволяет наглядно сравнивать числа и определять их порядок.

Что такое числовая прямая?

Числовая прямая — это геометрическая модель, представляющая все действительные числа на бесконечной прямой. Она используется для визуализации и работы с числами в математике.

Какие понятия связаны с числовой прямой?

На числовой прямой можно определить различные понятия, такие как точка, отрезок, интервал, положительные и отрицательные числа, а также нуль. Точка представляет отдельное значение на числовой прямой, отрезок — участок между двумя точками, интервал — непрерывный участок чисел на прямой. Положительные числа находятся справа от нуля, отрицательные — слева.

Как используется числовая прямая в математике?

Числовая прямая используется в математике для решения различных задач и выражения математических отношений. Она помогает визуализировать и понять числовые величины, их порядок и отношения. На числовой прямой можно отображать операции сложения, вычитания, умножения и деления, а также сравнивать числа и решать уравнения. Она также используется в физике, экономике и других областях, связанных с числами и их измерениями.