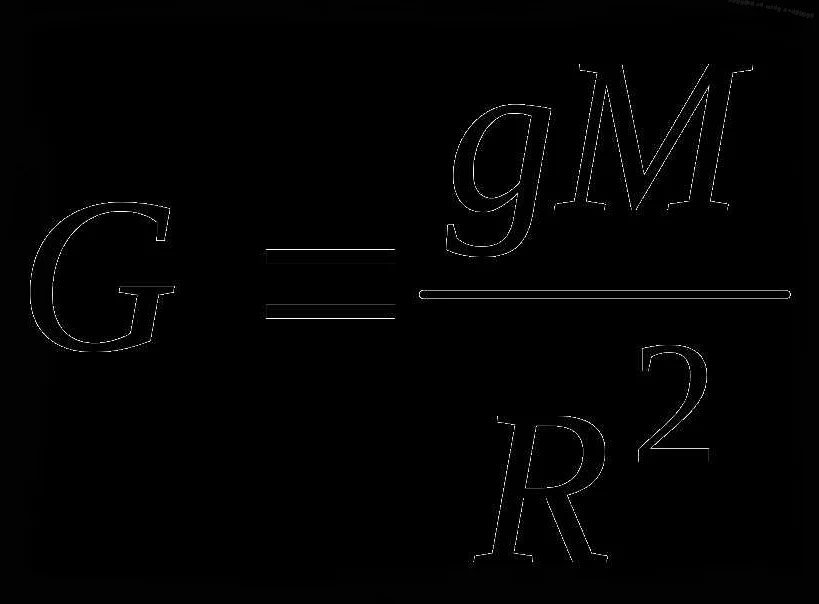Значение стрелок в математике: объяснение принятых обозначений

Стрелки в математике – это символы, обозначающие различные математические операции и сравнения. В статье рассказывается об основных типах стрелок и их значениях. Полезная информация для учеников и студентов, изучающих математику.

Стрелки используются в математике для обозначения векторов и направления. Они могут быть полезны при решении задач геометрии, физики и других наук.

Вектор – это математическое понятие, обозначающее направление и длину. Он обычно изображается в виде стрелки, которая указывает на направление вектора, а длина стрелки соответствует длине вектора. С помощью векторов можно решать различные задачи, например, определять путь движения тела, скорость, ускорение и т.д.

Стрелки также используются для обозначения направления. В этом случае стрелка указывает на то, как нужно двигаться – вправо, влево, вверх или вниз. Они также могут быть использованы для обозначения углов и других элементов геометрических фигур.

В этой статье мы рассмотрим наиболее распространенные примеры использования стрелок в математике и дадим объяснения, как правильно их интерпретировать.

Стрелки в математике

Стрелки в математике имеют важное значение, они используются для указания направления, перехода от одного значения к другому и для обозначения векторов. Стрелка может быть изображена как над символом, так и внизу или справа от него.

Стрелка над символом в математике обычно используется для обозначения производной. Например, если у нас есть функция y = f(x), то символ y’ с верхней стрелкой будет обозначать производную функции y по x.

Стрелка внизу или справа от символа может использоваться для обозначения целевой переменной в уравнении. Например, если у нас есть уравнение 2x + 1 = y, то стрелка справа от y будет означать, что мы ищем значение переменной y.

Векторы также могут быть обозначены стрелками в математике. Вектор – это направленный отрезок, который имеет определенную длину и направление. С помощью стрелок можно указать направление вектора и длину. Например, вектор А может быть обозначен как A→, где стрелка указывает направление и длину вектора.

В заключении, стрелки в математике являются важным инструментом, который используется для указания направления, перехода от одного значения к другому, а также для обозначения векторов.

Что это такое?

Стрелки в математике представляют собой символы, которые используются для обозначения направления от точки A до точки B. Они характеризуются двумя параметрами: направлением и длиной.

В математике могут быть использованы различные типы стрелок, например, однонаправленные стрелки, двунаправленные стрелки, «лучи» и т.д. Кроме того, стрелки могут быть применены для обозначения векторов, углов, точность измерений и других математических концепций.

Стрелки являются важным элементом графического языка в математике, который позволяет более наглядно и понятно представить различные математические концепции и выражения.

Какие бывают стрелки?

Стрелки – это символы, которые используются в математике для обозначения направления, векторов, операций и др. В зависимости от назначения, стрелки могут иметь различный вид и оформление.

Стрелки для обозначения направления: Это наиболее распространенный вид стрелок в математике. Они используются для обозначения направления движения, направление осей координат, стороны угла и т.д. Такие стрелки часто обозначаются символом «→».

Стрелки для обозначения векторов: Вектор – это математический объект, который имеет направление и длину. Для обозначения векторов используются стрелки с надписью в виде буквы или слова. Обычно эти стрелки имеют символ «→» над буквой.

Стрелки для обозначения операций: В математике часто используются стрелки для обозначения различных операций. Например, стрелка вверх используется для обозначения возведения в степень, стрелка вниз – для обозначения извлечения корня. Также существуют стрелки для обозначения суммы, разности, произведения и т.д.

Если вы знакомы с математикой, то, вероятно, вы знаете, что бывает множество видов стрелок. Надеемся, что данное объяснение вам помогло освоиться в этом вопросе.

Значение стрелок в геометрии

Стрелки в геометрии используются для обозначения направления движения, направления векторов или просто для указания важной информации в графическом изображении.

Например, стрелки часто используются при изображении векторов в геометрических задачах. В этом случае, направление стрелки указывает на направление вектора, а длина стрелки соответствует длине вектора. Стрелки могут быть как однородными, так и неравномерными, в зависимости от того, какой параметр отображается.

Стрелки могут также использоваться для указания направления движения объекта в пространстве. Это часто обнаруживается на картах и схемах, где отображаются пути движения поездов, самолетов или кораблей. В этом случае, стрелки служат важным инструментом для визуализации информации, которая может быть необходима для понимания местоположения и перемещения в пространстве.

Наконец, стрелки могут также использоваться для обозначения важной информации в графических изображениях. Например, стрелка может указывать на место расположения ключевой информации, важного объекта или деталя, которые необходимо заметить при просмотре изображения.

Таким образом, стрелки имеют множество применений в геометрии и могут быть использованы на различных уровнях анализа и отображения информации. Важно уметь использовать их правильно для максимальной эффективности в представлении и передачи информации.

Примеры использования

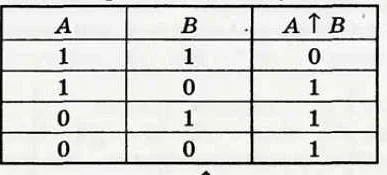
Стрелки играют важную роль в геометрии. Они помогают определить направления и углы. Например, стрелки могут быть использованы для обозначения векторов на графиках. На графиках они часто используются для указания направления движения объекта или направленности силы.

В математике стрелки могут использоваться для обозначения отношений между числами. Положительные числа обозначаются стрелкой, которая указывает вверх, а отрицательные числа обозначаются стрелкой, которая указывает вниз. Эта нотация часто используется при решении математических задач и при построении графиков функций.

Еще одним примером использования стрелок является обозначение углов на геометрических фигурах. Например, углы могут быть обозначены двумя стрелками, которые указывают на начало и конец угла.

Стрелки также могут использоваться для обозначения порядка следования элементов в последовательности или ряду. Например, стрелки могут быть использованы для обозначения возрастающей или убывающей последовательности чисел или элементов.

Кроме того, стрелки могут быть использованы для обозначения уровня или диапазона значений при работе с графиками или диаграммами. Например, на графике может быть обозначено, что стрелка вверх указывает на более высокие значения, а стрелка вниз – на более низкие значения.

Значение стрелок в алгебре

В алгебре стрелки часто используются для обозначения операций между математическими выражениями. Например, стрелка вида → обозначает присваивание значения переменной. Если, например, наша переменная x равна 5, то запись x → 5 означает, что мы присваиваем переменной x значение 5.

Еще одним примером является стрелка, обозначающая отображение (функцию). Если у нас есть функция f(x), то запись f: X → Y говорит нам, что функция f отображает множество X на множество Y, т.е. каждому элементу x из множества X сопоставляется элемент y из множества Y.

Также стрелки могут использоваться для обозначения отношений между объектами. Например, стрелка вида ⊂ обозначает отношение подмножества. Если у нас есть множество A, содержащее элементы a, b и c, и множество B, содержащее элементы a и b, то запись B ⊂ A означает, что множество B является подмножеством множества A.

• Стрелки в алгебре используются для обозначения операций между математическими выражениями.
• Одним из примеров использования стрелок является обозначение присваивания значения переменной.
• Стрелки могут использоваться для обозначения отображений (функций) и отношений между объектами.

Примеры использования

Угол: Отметим направление угла от основания к вершине стрелкой. Например, если угол BAC является прямым углом, то стрелка BA указывает на основание угла, а стрелка AC указывает на вершину угла.

Направление движения: Стрелки используются для обозначения направления движения, например, на диаграммах графиков. Направление стрелки может указывать на рост или уменьшение значения.

Вектор: В математике стрелки могут использоваться для обозначения векторов. Вектор — это направленный отрезок. Стрелка указывает на направление вектора, а длина стрелки указывает на его длину.

Пропорция: Стрелки могут использоваться для обозначения пропорций. Например, если у нас есть два сегмента, и мы хотим показать, что один сегмент в два раза длиннее другого, мы можем нарисовать стрелку, которая указывает на более длинный сегмент, и рядом с ней написать «2».

Пересечение графиков: Стрелки используются для обозначения точек пересечения на графиках. Например, если мы имеем два графика функций, стрелки могут помочь указать точки их пересечения и показать, где графики пересекаются.

Значение стрелок в тригонометрии

Стрелки в тригонометрии играют важную роль в определении углов и построении графиков тригонометрических функций. Одна из таких стрелок — это главная стрелка.

Главная стрелка — это радиус единичной окружности, начинающийся в точке (1,0) и направленный в положительном направлении оси x. Она используется для определения значений тригонометрических функций с углами кратными 90 градусам.

Стрелки синуса и косинуса тригонометрического круга угла тоже имеют определенное значение. Синус угла — это отношение противолежащей стороны к гипотенузе, а косинус угла — это отношение прилежащей стороны к гипотенузе. Если угол равен 0 градусов, то значение косинуса равно 1, а синуса равно 0.

• Стрелка синуса — вертикальная и направлена вверх, если 0° ≤ угол ≤ 180°. В противном случае, она направлена вниз.
• Стрелка косинуса — горизонтальная и направлена вправо, если 0° ≤ угол ≤ 90° и 270° ≤ угол ≤ 360°. В противном случае, она направлена влево.

Зная значения стрелок синуса и косинуса тригонометрического круга, можно определить значения любой другой тригонометрической функции для данного угла. Например, тангенс угла — это отношение синуса угла к косинусу угла.

УголСинусКосинусТангенс

0°	0	1	0
30°	1/2	√3/2	√3/3
45°	√2/2	√2/2	1
60°	√3/2	1/2	√3
90°	1	0	не определен

Вывод: стрелки в тригонометрии играют важную роль в определении углов и тригонометрических функций. Зная значение стрелок, можно определить значения других тригонометрических функций для данного угла, а также построить графики тригонометрических функций.

Примеры использования

Стрелки в математике используются для обозначения различных математических понятий. Например:

1. Векторы. Стрелки используются для обозначения направления вектора. Например, вектор a может быть представлен как →a.
2. Углы. Стрелка обозначает угол. Если угол величину, это обозначается как ∠ABC, где A, B и C — точки на окружности, образующие угол.
3. Векторные пространства. Векторы в векторных пространствах также обозначаются со стрелкой. Например, →u и →v могут быть векторами в трехмерном пространстве.
4. Градиент. Стрелка используется для обозначения направления градиента функции. Например, ∇f/∇x может быть представлено как →grad f.

Стрелки могут также использоваться для обозначения отношений между числами, например:

• Неравенства. Стрелка может быть использована для обозначения неравенства между двумя числами. Например, 3 < →x означает, что x больше 3.
• Функции. Стрелка используется для обозначения отображения между множествами. Например, f: X → Y означает, что значение функции f(x) находится в множестве Y при использовании аргумента x из множества X.
• Равенства. Стрелка может быть использована для обозначения равенства между двумя объектами. Например, a = →b означает, что a и b равны величине..

Обозначение стрелок в уравнениях

Стрелки в математике играют важную роль при записи уравнений и неравенств. Они обозначают разные математические операции и помогают понимать, какие действия нужно выполнить для решения задачи.

Стрелка вправо «→» часто используется для обозначения присваивания значения переменной или выражения. Например, a → 5 означает, что переменная a принимает значение 5.

Две стрелки вправо «⇒» используются для обозначения следствия в математике. Эта стрелка часто используется при доказательствах теорем и утверждений. Например, если у нас есть высказывание А ⇒ В, то это означает, что А является достаточным условием для В.

Стрелка влево «←» используется для обозначения противоположного числа. Например, если -x = 5, то можно записать как x ← -5.

Две стрелки влево «⇐» используются для обозначения необходимого условия. То есть если у нас есть высказывание А ⇐ В, то это означает, что А является необходимым условием для В.

• Стрелка вверх «↑» используется для обозначения наибольшего общего делителя.
• Стрелка вниз «↓» используется для обозначения наименьшего общего кратного.

Использование стрелок в математике помогает студентам учиться лучше понимать математические выражения и операции. Важно понимать значение каждой стрелки и знать, как правильно ее использовать для решения задач.

Как читать стрелки в линейных уравнениях?

Линейные уравнения часто имеют вид y = mx + b, где x — переменная, m — наклон (угол наклона прямой) и b — точка пересечения со осью y (интерсепт). Стрелки, указанные на значения, имеют важное значение при чтении и понимании линейных уравнений.

Стрелка наклона ( ↑ / ↓ ) — указывает на направление движения прямой. Для получения значения m следует разделить разность значений оси y и x на длину соответствующей стороны треугольника. Стрелка может указывать направление вверх (↑), если значение m положительное, и вниз (↓), если значение m отрицательное.

Стрелка интерсепта ( → / ← ) — указывает на расположение точки пересечения со осью y. Стрелка может указывать направление вправо (→), если значение b положительное, и влево дугимо (←), если значение b отрицательное.

При чтении линейных уравнений стоит уделить особое внимание стрелкам, чтобы понять направление прямой и точку пересечения с осью y, что поможет последующей работе с уравнением и графиком.

Как читать стрелки в системах уравнений?

Стрелки имеют важное значение в математике и системах уравнений. Как правило, стрелки используются для обозначения направления изменений или зависимостей в уравнениях. Они помогают понять, какие переменные зависят от других и как изменения в одной переменной влияют на другую.

В системе уравнений, обычно, используются две стрелки: «->» и «». Стрелка «->» обозначает прямую зависимость между переменными. Например, если есть уравнение «x -> y», оно означает, что переменная y зависит от переменной x. Если значение переменной x увеличивается, то значение переменной y также увеличивается.

Стрелка «» обозначает взаимозависимость между переменными. Например, если есть уравнение «x y», оно означает, что переменные x и y зависят друг от друга. Если значение переменной x увеличивается, то значение переменной y увеличивается, а если значение переменной y увеличивается, то значение переменной x тоже увеличивается.

Чтение стрелок в системе уравнений важно для понимания математических зависимостей и принятия правильных решений, поэтому необходимо уделить этому внимание при работе с математическими уравнениями.

Вопрос-ответ:

Какие значения могут иметь стрелки в математике?

Стрелки в математике могут иметь много различных значений, в зависимости от контекста, в котором они используются. Они могут обозначать направление, быстроту изменения, принадлежность к классу, какую-то функцию или отображение и многое другое. Например, стрелка над буквой может указывать на вектор или матрицу, а стрелка под знаком дроби может указывать на то, что дробь продолжается бесконечно.

Как использовать стрелки в алгебре?

В алгебре стрелки часто используются для обозначения правил преобразования выражений. Например, для обозначения умножения на число, используется стрелка под знаком умножения. Другой пример — стрелка над двумя выражениями может обозначать, что эти выражения эквивалентны, то есть могут быть заменены друг на друга в любом контексте.

Что такое стрелка на графике?

На графике стрелка может обозначать направление роста функции или её направление изменения векторного поля. Например, векторное поле может обозначаться с помощью стрелок, где направление их указывает направление изменения вектора в данной точке.

Что такое стрелки часов?

Стрелки часов — это объекты, которые обычно используются для измерения времени. Одна стрелка указывает на часы, а другая на минуты. Стрелки часов также могут использоваться в геометрии, например для обозначения угла между двумя лучами.

Как использовать стрелки для обозначения длины?

Стрелки могут быть использованы для обозначения длины отрезка. Например, для обозначения отрезка AB, можно нарисовать стрелки на концах этого отрезка. Кроме того, стрелки могут быть использованы для обозначения векторов, которые также могут иметь длину и направление.

Как использовать стрелки для обозначения порядка следования операций?

Стрелки могут быть использованы для обозначения порядка следования операций. Например, если нужно сначала умножить число на 2, а затем прибавить к нему 5, можно записать это так: 2x->+5. Здесь стрелка указывает на порядок выполнения операций.

Как использовать стрелки для обозначения принадлежности множеству?

Стрелки могут быть использованы для обозначения принадлежности множеству. Например, если нужно указать, что число 4 принадлежит множеству целых чисел, можно записать это так: 4 ∈ Z. Слово «принадлежит» здесь заменяется на символ стрелки с чертой сверху, который обозначает принадлежность.

Видео по теме: