Участки движения что это такое в математике

Участки движения в математике – это промежутки на числовой оси, на которых функция меняет свое значение. В данной статье рассматривается понятие участков движения и их влияние на поведение функции. Здесь вы найдете объяснение основных понятий и примеры, которые помогут вам лучше понять эту тему и применить ее на практике.

Участки движения – это понятие, которое широко используется в математике. Оно помогает описать и понять различные виды движения и изменения величин.

В математике участок движения – это фрагмент графика функции или кривой, который указывает на изменение значений на определенном интервале времени или другой переменной. Такие участки могут быть прямыми или кривыми, графически представляться линиями или сплошными кривыми.

Участки движения могут быть использованы для анализа различных процессов и явлений. Например, они могут помочь в изучении траектории движения тела, процессе изменения температуры или скорости роста популяции.

Участки движения представляют собой важный инструмент для математического анализа и моделирования различных явлений. Они позволяют увидеть и описать изменения, которые происходят во времени или в других переменных, и помогают нам лучше понять и предсказать мир вокруг нас.

Участки движения: что это такое в математике? Научные и популярные материалы

В математике участок движения представляет собой интервал времени или пространства, внутри которого происходит изменение позиции, скорости или ускорения объекта. Участки движения могут быть положительными, когда объект движется вперед, или отрицательными, когда объект движется назад.

Для описания участков движения часто используются математические функции, такие как функция положения, функция скорости и функция ускорения. Функция положения задает зависимость позиции объекта от времени или пространства, функция скорости — зависимость скорости от времени или пространства, а функция ускорения — зависимость ускорения от времени или пространства.

Участки движения могут быть изучены и анализированы с помощью математических методов, таких как дифференциальное и интегральное исчисления. Например, для определения средней скорости на участке движения можно использовать интеграл функции скорости, а для определения изменения позиции на участке движения можно использовать интеграл функции положения.

Участки движения находят применение в различных областях, включая физику, механику, астрономию и экономику. Они позволяют анализировать и предсказывать поведение объектов, их перемещение и взаимодействие.

Научные и популярные материалы об участках движения предлагают различные подходы и методы для изучения этой темы. Они могут включать иллюстрации, графики и задачи с примерами реальных ситуаций, чтобы помочь читателям лучше понять и применить понятия участков движения в своей жизни и работе.

Видео по теме:

Определение участков движения

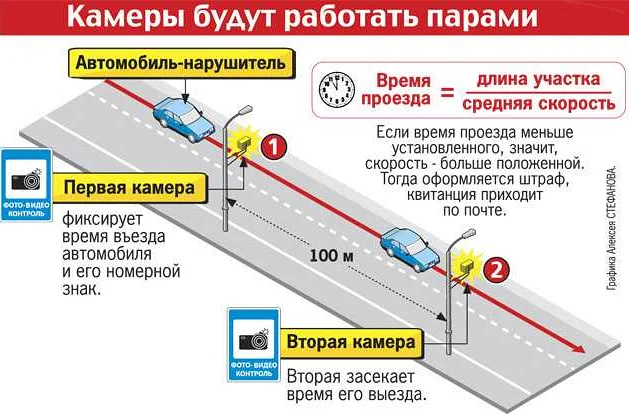
Чтобы определить участок движения, необходимо знать начальное положение объекта, его скорость и время, в течение которого происходит перемещение. Начальное положение обычно обозначается числом или точкой на числовой прямой, а скорость может быть задана как постоянная величина или как функция времени.

Участки движения могут иметь разную форму и длительность. Например, объект может двигаться с постоянной скоростью прямолинейно, что приводит к линейной форме участка движения. Он также может изменять скорость или направление движения, что приводит к криволинейной форме участка движения.

Участки движения могут быть изучены с помощью математических методов, таких как дифференциальное и интегральное исчисление. Они играют важную роль в физике, механике и других науках, где они помогают описать и предсказать движение объектов и систем.

ПонятиеОписание

Участок движения	Часть пути, которую объект проходит в определенный промежуток времени.
Начальное положение	Начальное положение объекта на числовой прямой или в пространстве.
Скорость	Скорость объекта, заданная как постоянная величина или функция времени.

Значение участков движения в математике

В математике участок движения может быть представлен в виде графика или функции, который показывает зависимость одной величины от другой. Например, график функции может показывать изменение скорости тела в зависимости от времени или изменение цены товара в зависимости от спроса.

Участки движения позволяют решать различные задачи, связанные с изменением величин. Например, с их помощью можно определить момент, когда величина достигнет определенного значения, найти точку экстремума функции или определить интервалы, на которых функция монотонно возрастает или убывает.

Также участки движения могут использоваться для моделирования различных процессов. Например, с их помощью можно описать движение тела в пространстве, изменение цен на рынке, распространение болезни в популяции и многое другое.

Изучение участков движения позволяет получить более глубокое понимание изменения величин и выявить закономерности в их поведении. Это позволяет прогнозировать будущие значения величин, оптимизировать процессы и принимать обоснованные решения на основе анализа данных.

В итоге, участки движения играют важную роль в математике и позволяют описывать и анализировать изменение величин в различных областях знания.

Примеры участков движения

В математике участком движения называется промежуток времени, в течение которого объект изменяет свое положение. Рассмотрим несколько примеров участков движения:

1. Движение прямолинейное равномерное: объект движется по прямой линии с постоянной скоростью. Например, автомобиль движется по прямой дороге без остановок.
2. Движение прямолинейное неравномерное: объект движется по прямой линии с изменяющейся скоростью. Например, птица, летящая вдоль прямой траектории и изменяющая свою скорость.
3. Движение по окружности: объект движется по окружности с постоянной скоростью. Например, спортсмен, бегущий по круговой дорожке.
4. Движение по спирали: объект движется по спирали, при этом его скорость может быть как постоянной, так и изменяющейся. Например, улитка, ползущая по стеблю растения.
5. Движение по параболе: объект движется по параболе, при этом его скорость может быть как постоянной, так и изменяющейся. Например, мяч, брошенный под углом к горизонту.

Это лишь некоторые примеры участков движения, которые могут быть рассмотрены в математике. Изучение движения объектов позволяет лучше понять законы физики и развитие науки в целом.

Математические свойства участков движения

Одно из важных математических свойств участков движения – это их длина. Длина участка движения определяется как сумма длин всех его отрезков. Это позволяет нам измерить протяженность участка и сравнивать его с другими участками движения.

Еще одно свойство участков движения – это их направление. Направление задается вектором, указывающим на то, куда направлен участок движения. Вектор направления можно использовать для определения различных характеристик движения, таких как скорость, ускорение и траектория.

Кроме того, участки движения могут иметь определенные геометрические формы, такие как прямые линии, кривые и окружности. Эти формы могут быть математически описаны и использоваться для предсказания поведения объекта на участке движения.

Также важным свойством участков движения является их продолжительность. Продолжительность участка определяется временем, затраченным на его прохождение. Это позволяет нам изучать зависимость скорости и времени на участке движения и анализировать его эффективность.

В целом, математические свойства участков движения позволяют нам более глубоко изучать и анализировать движение объектов в пространстве. Эти свойства могут быть использованы для решения различных задач, связанных с физикой, техникой, экономикой и другими областями науки и техники.

Значение участков движения в научных исследованиях

Исследование участков движения позволяет установить закономерности и особенности движения объектов. Это важно для понимания физических процессов, а также для разработки моделей и прогнозирования поведения объектов в будущем.

В математике участки движения играют особую роль в изучении функций, графиков и производных. Анализ участков движения позволяет определить скорость, ускорение и другие характеристики движения объекта в конкретные моменты времени.

Значение участков движения в научных исследованиях заключается в том, что они позволяют получить детальную информацию о движении объектов и выявить скрытые закономерности. Это помогает ученым лучше понять и описать реальные физические и математические явления.

Популярные материалы о участках движения

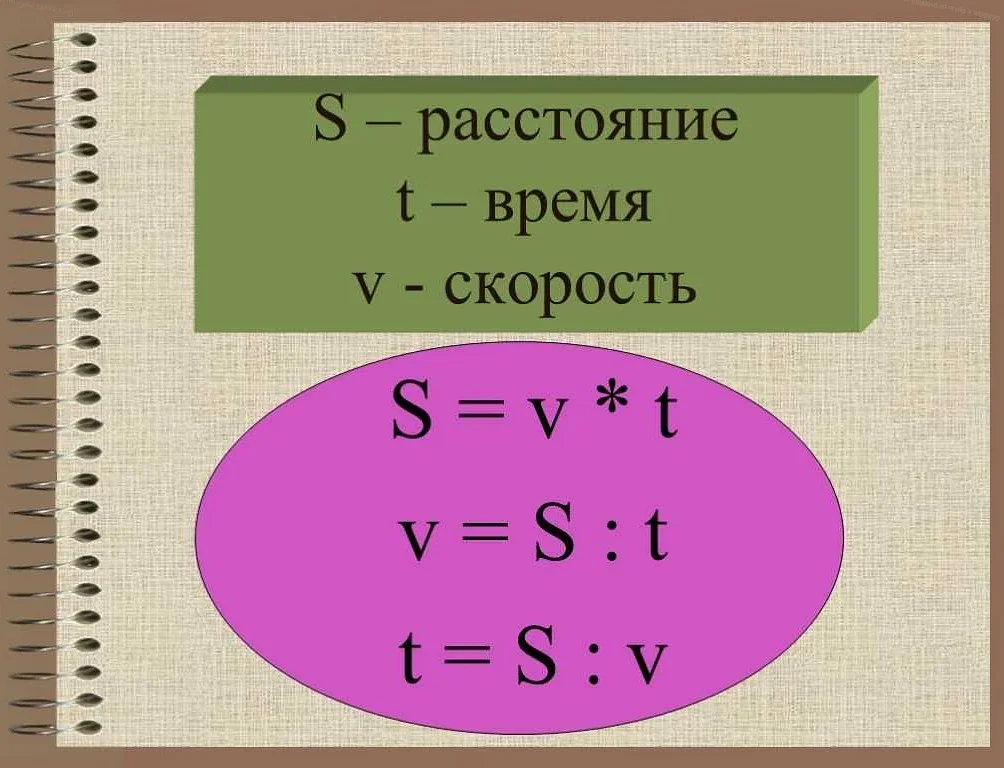
Если вы хотите более подробно изучить эту тему, вам могут пригодиться следующие популярные материалы:

Векторная физика	На странице Википедии посвященной векторной физике вы сможете найти информацию о векторах и их применении в описании движения объектов.
Одномерное движение	На сайте Khan Academy вы сможете найти курс по одномерному движению, в котором детально рассматривается понятие участков движения и их применение в различных задачах.
Движение по окружности	На странице Википедии описывается движение по окружности и вводится понятие участков движения на данном типе траектории.

Эти материалы помогут вам лучше понять суть участков движения и применение этого понятия в различных областях науки.

Как использовать участки движения в повседневной жизни?

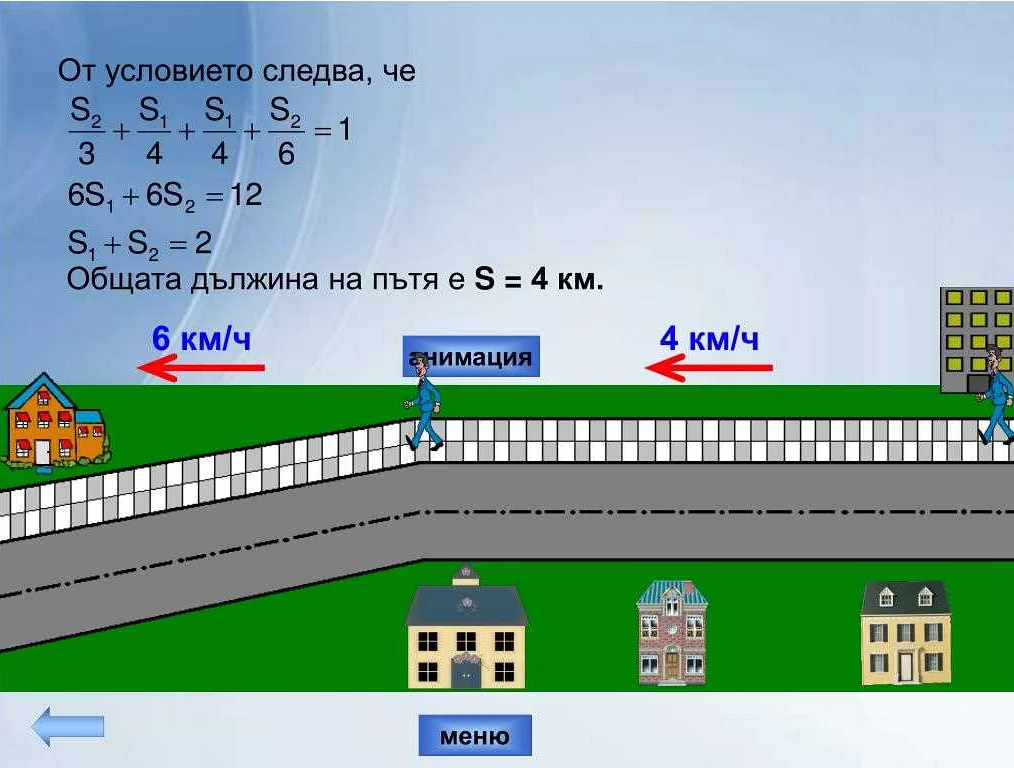
Участки движения имеют широкий спектр применения в повседневной жизни. Вот несколько способов, как использовать их:

1. Планирование маршрутов: Участки движения могут быть полезны при планировании маршрутов, особенно когда нужно выбрать оптимальный путь. Они могут помочь определить участки с наименьшими препятствиями или наиболее эффективные пути для достижения заданной цели.
2. Оптимизация процессов: Участки движения могут помочь оптимизировать процессы в повседневной жизни. Например, они могут помочь определить оптимальный путь для выполнения задач или организации рабочего пространства.
3. Предсказание поведения: Участки движения могут быть использованы для предсказания поведения объектов или процессов. Например, они могут помочь предсказать движение транспорта на дороге или поток покупателей в магазине.
4. Оценка рисков: Участки движения могут быть полезны при оценке рисков в различных ситуациях. Например, они могут помочь определить наиболее опасные места на дороге или наиболее вероятные места возникновения аварий.
5. Анализ данных: Участки движения могут быть использованы для анализа данных и выявления закономерностей. Например, они могут помочь исследователям определить взаимосвязь между движением людей и распространением инфекционных заболеваний.

В целом, участки движения представляют собой мощный инструмент, который может быть применен во многих сферах жизни. Они помогают принимать обоснованные решения и оптимизировать процессы, что в свою очередь способствует повышению эффективности и улучшению качества жизни.

Выводы о участках движения в математике

В математике участки движения играют важную роль в анализе функций и графиков. Они помогают понять изменения значений функции на определенном интервале и определить направление движения графика.

Основные выводы о участках движения в математике:

• Участок движения — это интервал на графике функции, где функция изменяется в определенном направлении.
• Возрастающий участок — это интервал, на котором значения функции увеличиваются по мере увеличения аргумента.
• Убывающий участок — это интервал, на котором значения функции уменьшаются по мере увеличения аргумента.
• Точка экстремума — это точка на графике функции, где функция достигает максимального или минимального значения.
• Переломный участок — это интервал, на котором функция меняет свое направление движения.
• Горизонтальный участок — это интервал, на котором значения функции остаются постоянными.

Изучение участков движения позволяет более глубоко анализировать функции и предсказывать их поведение. Это важный инструмент для решения задач и построения графиков функций.

Вопрос-ответ:

Какие существуют участки движения в математике?

В математике существуют различные участки движения, такие как прямолинейное движение, круговое движение, сложное движение и др.

Что такое прямолинейное движение?

Прямолинейное движение — это движение по прямой линии.

Какие примеры прямолинейного движения можно найти в реальной жизни?

Примеры прямолинейного движения в реальной жизни включают движение автомобиля по прямой дороге, движение летящего стрелка и др.

Что такое круговое движение?

Круговое движение — это движение по окружности или дуге окружности.

Какие примеры кругового движения можно найти в реальной жизни?

Примеры кругового движения в реальной жизни включают движение спутника вокруг Земли, движение колеса велосипеда и др.

Что такое участки движения в математике?

Участки движения в математике — это интервалы, на которых меняется скорость движения объекта. В пределах каждого участка движения скорость остается постоянной.

Как определить участки движения объекта?

Для определения участков движения объекта необходимо проанализировать его скорость в разные моменты времени. Если скорость остается постоянной на протяжении некоторого интервала времени, то можно сказать, что объект движется с постоянной скоростью на этом участке.