Что значат 3 точки в математике

3 точки в математике — это символ, обозначающий бесконечность или неполноту в математических выражениях и последовательностях. Узнайте, как использовать 3 точки для обозначения суммы, произведения и других математических операций.

В математике тройная точка, также известная как многоточие, является важным элементом, который используется для обозначения пропущенных частей в последовательностях, числах или выражениях. Она обозначает, что в данном месте можно продолжить последовательность, развивая или дополняя ее.

Тройная точка имеет свои особенности и применяется в разных областях математики. В теории множеств она используется для обозначения бесконечных последовательностей или множеств. В анализе она может обозначать бесконечные суммы или интегралы. В геометрии тройная точка может указывать на продолжение линии или на наличие дополнительных точек на плоскости.

Пример использования трех точек в математике: сумма чисел от 1 до 100 равна 1 + 2 + 3 + … + 98 + 99 + 100.

Однако, следует отметить, что тройная точка может иметь разные значения в различных контекстах. Некоторые математические дисциплины могут использовать ее для обозначения конкретных последовательностей или выражений, в то время как другие могут использовать ее для указания на общую закономерность или обобщение.

В заключение, тройная точка в математике является мощным инструментом, который позволяет сократить запись и указать на продолжение или обобщение последовательности, числа или выражения. Она используется в разных областях математики и имеет свои особенности в каждой из них. Понимание значения трех точек помогает улучшить понимание и применение математических концепций и теорий.

Значение трех точек в математике

Тройные точки, также известные как многоточие или эллипсис, играют важную роль в математике и широко используются для обозначения различных математических концепций.

Во-первых, тройные точки могут использоваться для обозначения бесконечных последовательностей или сумм. Например, сумма всех натуральных чисел можно записать как:

1 + 2 + 3 + 4 + 5 + …

или с использованием трех точек:

1 + 2 + 3 + 4 + 5 + …

Тройные точки также могут указывать на то, что последовательность продолжается в бесконечность, и представляют собой сокращенную форму записи.

Во-вторых, тройные точки могут использоваться для обозначения вырожденных или повторяющихся паттернов. Например, принято записывать выражение «и так далее» с помощью трех точек:

a, b, c, … , x, y, z, …

где a, b, c — первые несколько элементов последовательности, а x, y, z — элементы, следующие после этого паттерна.

Тройные точки также могут использоваться для обозначения пропущенных частей или диапазонов в последовательностях. Например, последовательность всех четных чисел можно записать как:

2, 4, 6, 8, …

или с использованием трех точек:

2, 4, 6, 8, …

Такое использование трех точек позволяет сделать запись более компактной и удобной.

В заключение, тройные точки являются важным инструментом в математике и используются для обозначения бесконечных последовательностей, вырожденных паттернов и пропущенных частей в последовательностях. Они позволяют сделать запись более лаконичной и упрощают понимание математических концепций.

Видео по теме:

Основные понятия трех точек

Одно из применений трех точек — определение прямой. Если три точки лежат на одной прямой, то говорят, что они коллинеарны. Если же они не лежат на одной прямой, то говорят, что они неколлинеарны.

Еще одно важное понятие, связанное с тройкой точек, — это треугольник. Треугольник — это геометрическая фигура, образованная тремя отрезками, соединяющими три точки. Треугольник может быть различных типов, в зависимости от своих сторон и углов.

Тройка точек также используется в алгебре для определения плоскости. Если три точки не лежат на одной прямой, то они определяют плоскость. Трехмерная плоскость можно представить как поверхность, проходящую через эти три точки.

Таким образом, тройка точек играет важную роль в математике, позволяя определить прямые, треугольники и плоскости. Понимание основных понятий трех точек является фундаментом для дальнейшего изучения геометрии и алгебры.

Принципы использования трех точек

В математике троечка точек обозначает многоточие или эллипсис и используется для обозначения пропущенных частей выражения или последовательности.

Основные принципы использования трех точек:

1. Обозначение пропущенной части выражения или последовательности: троечка точек может быть использована, чтобы указать на пропущенные части выражения или последовательности. Например, если есть последовательность чисел от 1 до 10, то можно записать ее как 1, 2, 3, …, 10.
2. Обозначение бесконечной последовательности: троечка точек может быть использована, чтобы указать на бесконечную последовательность. Например, если есть последовательность натуральных чисел, можно записать ее как 1, 2, 3, ….
3. Обозначение пропущенных частей доказательств: троечка точек может быть использована в доказательствах для обозначения пропущенных частей. Например, если в доказательстве есть несколько шагов, но не все из них приведены, то можно записать их как шаг 1, шаг 2, …, шаг n-1, …, шаг n.

Важно отметить, что троечка точек не является математической операцией и не имеет точного значения в числовом смысле. Ее значение определяется контекстом использования.

Вопрос-ответ:

Зачем в математике используются три точки?

Три точки в математике используются для обозначения бесконечной последовательности или множества значений. Они указывают на то, что последовательность продолжается или множество не полностью перечислено.

Какое значение имеют три точки в математических уравнениях?

В математических уравнениях три точки могут использоваться для обозначения пропущенных частей или неопределенных выражений. Они показывают, что уравнение продолжается или содержит бесконечное количество решений.

Для чего используются три точки в математической статистике?

В математической статистике три точки часто используются для обозначения диапазона значений или разброса данных. Например, в интервальной оценке дисперсии или стандартного отклонения может использоваться обозначение «x̄ ± 3σ», где «x̄» — среднее значение, а «σ» — стандартное отклонение.

Каким образом три точки связаны с алгеброй и геометрией?

В алгебре и геометрии три точки могут использоваться для определения линий, плоскостей и многогранников. Например, для задания прямой в трехмерном пространстве можно использовать две точки и направляющий вектор, а для определения плоскости достаточно трех неколлинеарных точек.

В каких случаях три точки могут быть использованы для обозначения векторов?

Три точки могут быть использованы для обозначения векторов в случае, когда нам известно начальное положение точки и ее конечное положение. В этом случае три точки могут быть использованы для задания направления и длины вектора.

Что означают три точки в математике?

В математике три точки обозначают троеточие или многоточие. Они указывают на продолжение последовательности или набора чисел, которое можно вывести или дополнить.

Применение трех точек в геометрии

В геометрии трех точек, выраженных в виде символа «…» или «…», используются в различных контекстах и имеют различные значения.

Одно из наиболее распространенных применений трех точек в геометрии – это обозначение прямой, продолжающейся в бесконечность. Троечка точек в этом случае указывает на то, что прямая продолжается вне пределов отображаемой области и не имеет конечного конца. Это важное понятие в геометрии, так как позволяет визуализировать и анализировать бесконечные линии и поверхности.

Троечка точек также может использоваться для обозначения пропуска в последовательности точек или чисел. Например, если имеется последовательность точек или чисел, образующих арифметическую или геометрическую прогрессию, и пропущена одна или несколько точек или чисел, то троечка точек может быть помещена между соседними элементами для обозначения пропуска. Это помогает визуально указать на шаблон последовательности и обозначить пропущенные элементы.

Еще одним применением трех точек в геометрии является обозначение плоскости или поверхности, продолжающейся за пределами отображаемой области. Троечка точек в этом случае указывает на то, что плоскость или поверхность простираются вне видимой области и не имеют ограничений в пространстве.

Таким образом, троечка точек в геометрии имеет различные значения и применяется для обозначения бесконечности, пропуска элементов в последовательности и продолжения плоскости или поверхности за пределами отображаемой области.

Применение трех точек в алгебре

Точки в алгебре могут иметь различные значения и играть важную роль в решении различных задач. Вот некоторые из основных способов использования трех точек в алгебре:

1. Обозначение бесконечности:

Три точки (…) могут использоваться для обозначения бесконечности в математических выражениях. Например, если сумма чисел неограничена, мы можем записать ее в виде:

a1 + a2 + a3 + …

где троеточие указывает на продолжение ряда чисел до бесконечности.

2. Интервалы:

Точки также могут использоваться для обозначения интервалов чисел. Например, можно записать интервал от 1 до 10 следующим образом:

1, 2, 3, …, 10

где троеточие указывает на продолжение ряда чисел в данном интервале.

3. Арифметические прогрессии:

Троеточие может использоваться для обозначения арифметической прогрессии. Например, если нам дана арифметическая прогрессия с первым членом a и разностью d, мы можем записать ее следующим образом:

a, a + d, a + 2d, …

где троеточие указывает на продолжение прогрессии.

Все эти применения трех точек в алгебре позволяют упростить запись математических выражений и увеличить их ясность и компактность.

Применение трех точек в тригонометрии

Три точки (…) в тригонометрии используются для обозначения бесконечности или непрерывности. Они могут указывать на то, что функция или последовательность продолжается далее в бесконечность.

Например, в тригонометрической функции синус (sin), три точки (…) могут использоваться для обозначения периодического повторения функции. Синус имеет периодическую природу, и его значения повторяются на протяжении всей числовой оси. Поэтому функцию синуса можно представить в виде повторяющегося графика, обозначенного тремя точками (…).

Также, три точки (…) могут использоваться для обозначения непрерывности графика функции. Например, в функции тангенс (tan), график функции имеет вертикальные асимптоты в точках, где тангенс не определен. Однако, при приближении к этим точкам справа или слева, функция все равно имеет значения. Три точки (…) могут быть использованы для обозначения того, что функция тангенс непрерывна и продолжается за пределы вертикальных асимптот.

Таким образом, использование трех точек (…) в тригонометрии позволяет наглядно указать на бесконечность или непрерывность функции или последовательности, что облегчает понимание и анализ математических моделей.

Применение трех точек в аналитической геометрии

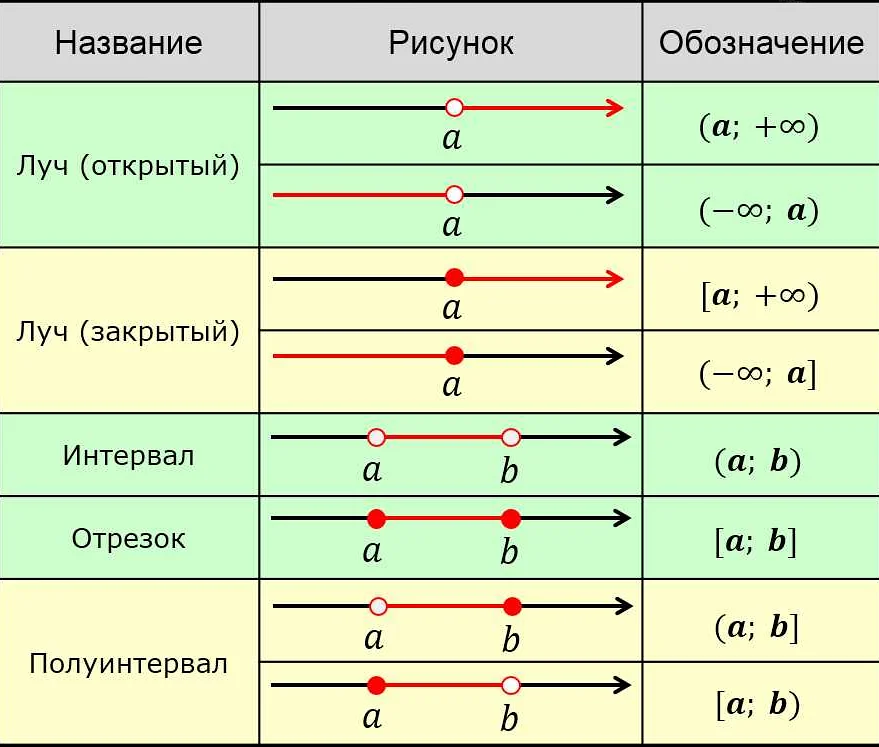
• Построение отрезка. При заданной начальной и конечной точке мы можем легко построить отрезок, используя трех точек. Это позволяет нам определить длину и направление отрезка.
• Нахождение середины отрезка. Зная две конечные точки отрезка, мы можем найти его середину, используя трех точек. Это полезно, когда нам нужно разделить отрезок пополам или найти точку, находящуюся на определенном расстоянии от одной из конечных точек.
• Нахождение угла. Трех точек можно использовать для определения угла между двумя отрезками. Это позволяет нам изучать геометрические фигуры, такие как треугольники и многоугольники, и решать задачи, связанные с их углами.
• Нахождение площади. Благодаря трех точкам мы можем вычислить площадь различных геометрических фигур, таких как треугольники, прямоугольники и круги. Это полезно при решении задач, связанных с площадью и объемом.
• Определение положения точки относительно прямой. При заданных трех точках мы можем определить, находится ли четвертая точка на прямой или вне ее. Это помогает нам изучать геометрические свойства прямых и определять их пересечения.

Применение трех точек в аналитической геометрии позволяет нам решать разнообразные задачи, связанные с геометрией. Они являются основой для изучения и понимания различных геометрических объектов и их свойств. Без трех точек было бы гораздо сложнее анализировать и решать геометрические задачи.

Применение трех точек в математическом анализе

Три точки, также известные как многоточие или троеточие, играют важную роль в математическом анализе. Они используются для обозначения бесконечных последовательностей и сумм.

Когда три точки используются в конце последовательности чисел или выражений, они обозначают, что последовательность продолжается в бесконечность. Например, если дана последовательность чисел 1, 2, 3, 4, …, то она может быть обозначена как 1, 2, 3, 4, … . Таким образом, троечка показывает, что последовательность продолжается далее, но не указывает, какие числа идут после.

Троечка также используется для обозначения суммы всех членов бесконечной последовательности. Например, если дана последовательность чисел 1, 2, 3, 4, …, то сумма всех членов этой последовательности может быть записана как 1 + 2 + 3 + 4 + … = … . Троечка показывает, что сумма продолжается в бесконечность.

Применение трех точек в математическом анализе позволяет удобно записывать и работать с бесконечными последовательностями и суммами. Они позволяют сделать запись более компактной и упрощают вычисления.