Что означает значок дуги в математике

Значок дуги в математике используется для обозначения угла между двумя линиями или отрезками. Узнайте, как читать и использовать этот символ в различных математических задачах.

Дуга — это фигура, образованная частью окружности. В математике дуга широко используется для обозначения связи между двумя точками на окружности или на плоскости. Значок дуги помогает нам указать направление и расстояние между этими точками.

В геометрии, значок дуги обычно обозначается двумя точками на окружности или на плоскости, соединенными дугой. Он может быть использован для обозначения угла, измеряемого в радианах, а также для указания промежуточных точек на окружности или на плоскости.

Например, если мы хотим указать угол между двумя линиями, мы можем использовать значок дуги для обозначения этого угла. Значок дуги позволяет нам указать меру угла и его направление.

В тригонометрии, значок дуги используется для обозначения угла и его меры в градусах или радианах. Он помогает нам определить связь между тригонометрическими функциями и углами.

Например, если мы хотим вычислить синус или косинус угла, мы можем использовать значок дуги для указания этого угла и его меры. Значок дуги помогает нам сопоставить углы с их тригонометрическими функциями.

В заключение, значок дуги в математике играет важную роль в указании связи между точками на окружности или на плоскости, а также в определении углов и их меры. Он является одним из основных инструментов для работы с геометрическими и тригонометрическими задачами.

Значение и применение значка дуги в математике

В математике значок дуги обозначает отрезок на окружности, ограниченный двумя точками. Дуга может быть полной, то есть занимать всю окружность, или же частичной, ограниченной углом, меньшим 360 градусов.

Значок дуги широко применяется в геометрии и тригонометрии. В геометрии он используется для обозначения углов и длин дуг на окружности. Например, при рассмотрении треугольника на плоскости, дуги могут обозначать углы между сторонами треугольника или между сторонами и радиусами окружности, описанной вокруг треугольника.

В тригонометрии дуги используются для определения тригонометрических функций. Например, синус угла определяется как отношение противолежащего катета к гипотенузе прямоугольного треугольника, а косинус угла — как отношение прилежащего катета к гипотенузе. Дуги помогают связать геометрические понятия с численными значениями.

Значок дуги также применяется в аналитической геометрии для обозначения длин дуг на координатной плоскости. Например, при построении графиков функций дуги могут отображать изменение значений функции в определенном интервале.

Таким образом, значок дуги имеет важное значение в математике и широко применяется для обозначения углов, длин дуг и значений тригонометрических функций. Он помогает визуализировать геометрические и численные свойства объектов и является основой для многих математических теорем и формул.

Роль дуги в геометрии

Дуги используются для измерения углов между лучами или отрезками, которые пересекают окружность. Угол, образованный дугой, называется центральным углом. Он измеряется в градусах и может быть как остроугольным, так и тупоугольным.

Дуги также используются при определении секторов окружности. Сектор — это фигура, ограниченная двумя лучами и дугой. Секторы помогают разделить окружность на части и упрощают вычисления площадей фигур.

Для работы с дугами в геометрии используются различные обозначения и символы. Например, дуга может быть обозначена двумя точками, находящимися на окружности, или с помощью специальных символов, таких как дуговая стрелка или дуговой значок.

В геометрии дуги являются важным инструментом для измерения углов и работы с окружностями. Они помогают определить углы и площади фигур, а также упростить вычисления и построения.

Использование дуги в тригонометрии

Использование дуги в тригонометрии позволяет вычислять значения тригонометрических функций (синуса, косинуса, тангенса и др.) для заданных углов. Дуга измеряется в радианах или градусах, и ее длина зависит от величины угла.

Для работы с дугой в тригонометрии используется таблица, которая содержит значения тригонометрических функций для разных углов. В таблице указывается значение синуса, косинуса, тангенса и других функций для каждого угла.

Угол (в градусах)СинусКосинусТангенс

0°	0	1	0
30°	1/2	√3/2	1/√3
45°	√2/2	√2/2	1
60°	√3/2	1/2	√3
90°	1	0	∞

Использование дуги в тригонометрии позволяет решать множество задач и проблем, связанных с измерением углов и вычислением значений тригонометрических функций. Например, с помощью дуги можно вычислить высоту недоступного объекта, определить расстояние между двумя точками на земле или решить задачу навигации.

Применение дуги в алгебре

Одно из основных применений дуги в алгебре — это представление угловых величин. Угол может быть измерен в радианах или в градусах. Дуга AB может представлять собой угол, измеренный от начальной точки A до конечной точки B на единичной окружности. Также дуга может быть использована для обозначения сектора, который представляет собой область между двумя радиусами и дугой на окружности.

Еще одно применение дуги в алгебре — это представление геометрических и алгебраических функций. Например, синус и косинус могут быть представлены в виде дуги на единичной окружности. Также дуга может использоваться для представления арктангенса, арккосинуса и арксинуса.

Дуга также может быть использована для представления логарифмических функций. Например, для представления простого логарифма можно использовать дугу с началом в единице и концом в числе, для которого нужно вычислить логарифм.

Таким образом, дуга имеет широкий спектр применений в алгебре и может быть использована для представления угловых величин, геометрических и алгебраических функций, а также логарифмических функций.

Значение дуги в статистике

В статистике дуга используется для представления различных видов данных, таких как распределение вероятности, частотность или процентное соотношение. Дуги обычно используются в круговых графиках или диаграммах, чтобы визуально отобразить относительные величины или пропорции различных категорий или групп данных.

Дуги в статистике могут быть представлены в виде секторов круга, где каждая дуга соответствует определенной категории или группе данных. Размер дуги может быть пропорциональным относительной величине данных или может быть задан вручную в соответствии с требованиями представления информации. Чем больше размер дуги, тем больше значение данной категории или группы данных.

Дуги в статистике могут быть использованы для представления множества различных данных, таких как доли населения разных групп, распределение доходов, пропорции результатов опроса и т. д. Они позволяют быстро и наглядно сравнивать разные категории данных и выявлять закономерности или отклонения в распределении или процентном соотношении данных.

Кроме того, дуги в статистике могут быть использованы для представления временных рядов или изменений в данных на протяжении определенного периода времени. Например, дуги могут быть использованы для представления изменений в составе населения или процентного соотношения продаж по категориям товаров в разные годы или кварталы.

В целом, дуги в статистике являются мощным инструментом для наглядного представления данных и анализа различных категорий или групп данных. Они позволяют сравнивать относительные величины, выявлять закономерности и отклонения, а также отображать изменения в данных на протяжении времени. Поэтому дуги широко используются в статистике и помогают наглядно представлять сложные данные и тенденции.

Дуга как элемент графического представления данных

В математике дуга представляет собой часть окружности, ограниченную двумя точками. Однако, помимо математических вычислений, дуга также активно используется в графическом представлении данных.

Дуга может быть применена для визуализации различных данных, таких как статистика, прогнозы, исследования и многое другое. Она позволяет наглядно представить информацию и сделать ее более понятной для аудитории.

Одним из основных применений дуги является построение круговых диаграмм. В таких диаграммах каждая дуга представляет собой долю от общего значения или процента. Часто дуги различной величины отображаются разными цветами или оттенками, что помогает визуально выделить различные категории данных.

Круговые диаграммы с использованием дуг также позволяют сравнивать данные между собой и выявлять зависимости. Например, если дуга одной категории занимает большую часть диаграммы, это может указывать на ее высокую значимость или доминирование в исследуемых данных.

Кроме того, дуги могут быть использованы для представления временных рядов или изменений данных во времени. При этом каждая дуга соответствует определенному временному периоду или шагу. Таким образом, можно наглядно отслеживать динамику изменения данных и выявлять тренды.

Использование дуг в графическом представлении данных помогает сделать информацию более доступной и понятной. Они позволяют увидеть визуальные связи и зависимости между данными, а также выделить ключевую информацию. Таким образом, дуги являются эффективным инструментом в анализе и визуализации данных в различных областях, включая науку, бизнес и образование.

Значение дуги в угловой мере

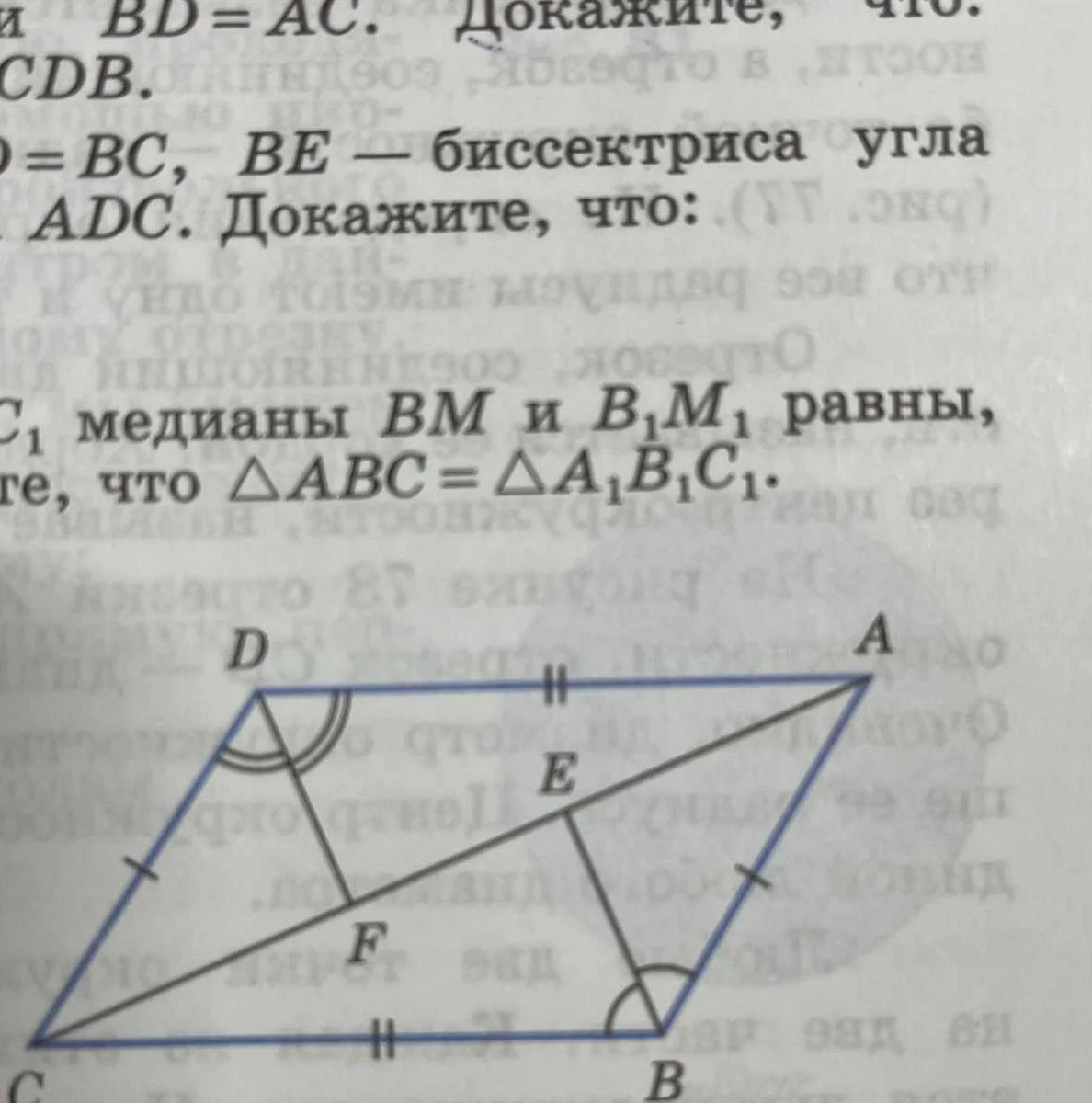
Для измерения дуг в угловой мере используется радиан. Радиан — это мера угла, при которой длина дуги равна радиусу окружности. Один радиан соответствует дуге, которая равна длине радиуса окружности.

Значение дуги в угловой мере выражается числом и может быть положительным или отрицательным. Положительное значение дуги указывает на поворот по часовой стрелке, а отрицательное значение — против часовой стрелки.

Дуги в угловой мере используются для решения различных задач, связанных с геометрией, физикой и другими областями науки. Например, они позволяют измерять углы в треугольниках, находить угловую скорость вращения тела и описывать гармонические колебания.

Использование дуг в угловой мере позволяет более точно определить положение и перемещение объектов, а также решать сложные задачи, связанные с углами и вращением.

Видео по теме:

Вопрос-ответ:

Зачем нужен значок дуги в математике?

Значок дуги используется для обозначения дуги на графике или окружности. Он позволяет легко проследить форму и положение дуги на плоскости.

Как правильно использовать значок дуги?

Чтобы использовать значок дуги, необходимо сначала определить начальную и конечную точки дуги. Затем, рисуя дугу, нужно следовать за направлением движения по окружности или графику. Начальную и конечную точки дуги обычно обозначаются специальными буквами или символами.

Где можно встретить значок дуги в математике?

Значок дуги может быть использован в различных областях математики. Например, он может быть использован для обозначения угла, дуги окружности, а также для построения графиков функций. Также значок дуги может быть использован в геометрии для обозначения дуги между двумя точками на плоскости.

Каким образом значок дуги может помочь в решении математических задач?

Значок дуги может помочь в решении математических задач, связанных с графиками функций и окружностями. Например, при анализе графика функции значение дуги может указывать на периодичность или симметрию функции. Также значок дуги может помочь визуализировать и понять геометрические свойства фигур и углов.

Применение дуги в физике и инженерии

Одним из применений дуги в физике является моделирование траектории движения объектов. Например, при изучении движения планет вокруг Солнца, дуга может быть использована для представления эллиптических орбит планет. Также дуга может использоваться для описания траектории движения проектайла или других объектов, брошенных под углом к горизонту.

В инженерии дуга также находит свое применение. Например, при проектировании дорожных развязок или строительстве мостов дуга может быть использована для определения формы и геометрии конструкции. Дуга также используется при моделировании течения жидкостей и газов, что позволяет инженерам предсказывать и анализировать различные физические процессы.

Таким образом, дуга является важным геометрическим понятием, которое находит применение в физике и инженерии. Ее использование позволяет моделировать и анализировать различные физические процессы, что является важным инструментом для развития науки и техники.

Дуга как символ в других науках и областях

Значение символа дуги используется не только в математике, но и в других науках и областях знания. Этот символ имеет свои особенности и интерпретации в разных контекстах.

В географии дуга может олицетворять границу между двумя территориями или регионами. Например, на картах мира дуга может обозначать границу между странами или континентами.

В астрономии символ дуги может указывать на траекторию движения небесных тел. Например, дуга может представлять орбиту планеты вокруг Солнца или траекторию кометы в космическом пространстве.

Дуга также является символом в различных областях искусства. В архитектуре дуга используется для создания арочных конструкций, которые придают зданиям или мостам особую красоту и стабильность. В живописи и дизайне дуга может быть использована как элемент композиции или декоративный узор.

В символике и религиозных верованиях дуга может иметь глубокий символический смысл. Например, в христианской традиции радуга ассоциируется с обетованием Божьим, которое было дано Ною после потопа.

Таким образом, символ дуги имеет широкое применение в различных науках и областях, отражая свои уникальные значения и интерпретации в каждой из них.