Что обозначает значок в математике

Значок в математике является символом или знаком, который представляет определенное математическое понятие или операцию. Он используется для обозначения различных математических операций, таких как сложение, вычитание, умножение и деление, а также для обозначения отношений между числами и переменными. Значки в математике также могут представлять специальные функции, константы или символы для обозначения множеств, пространств и операций в различных областях математики.

Значок — это специальный символ, который используется в математике для обозначения различных математических выражений и операций. Он позволяет наглядно представить сложные математические идеи и упростить запись формул.

В математике значок может обозначать различные вещи: от чисел и переменных до операций и отношений. Например, значок «x» может представлять неизвестное число или переменную, в то время как значок «+» обозначает операцию сложения. Значки могут быть использованы для обозначения выражений, формул и уравнений.

Одни значки могут быть более распространенными и широко используемыми, как, например, знаки «+», «-«, «*», «/», «=», «», а другие значки могут быть специфичными для определенных областей математики или научных дисциплин.

Использование значков в математике помогает упростить и улучшить понимание математических концепций. Значки позволяют строить логические цепочки и связи между различными элементами математических выражений и уравнений, а также сделать их более читаемыми и понятными для учеников и специалистов в области науки.

Значение значка в математике: основные понятия

Одним из наиболее распространенных значков в математике является символ «плюс» (+), который обозначает операцию сложения. Значок «минус» (-) обозначает операцию вычитания, а значок «умножить» (×) используется для обозначения умножения.

Значки также могут быть использованы для обозначения математических функций, таких как синус (sin), косинус (cos) и тангенс (tan). Например, для обозначения синуса используется символ «sin», за которым следует аргумент функции в круглых скобках.

Значки также могут представлять числа или переменные. Например, символ «π» представляет число Пи, а символ «x» может обозначать переменную в алгебре.

Значки в математике могут быть использованы для указания отношений между объектами. Например, символ «равно» (=) используется для обозначения равенства двух выражений или чисел. Значок «больше» (>) обозначает, что одно число больше другого, а символ «меньше» (

Значки в математике имеют свои строго определенные значения и правила использования. Понимание основных понятий и значений значков помогает в понимании и решении математических задач и уравнений.

Значение значка в математике: роль в выражении

В математике значки играют важную роль в выражении. Значки представляют собой символы или обозначения, которые используются для обозначения математических операций, переменных, констант и других элементов.

Значок может иметь различные значения в зависимости от контекста. Например, знак «+» может означать сложение, если он находится между двумя числами, или добавление, если он находится между строками или другими объектами.

В математических выражениях значки используются для обозначения операций, таких как сложение, вычитание, умножение и деление. Например, выражение «2 + 3» означает сложение чисел 2 и 3.

Значки также могут использоваться для обозначения переменных и констант. Например, буква «x» может использоваться в выражении для обозначения переменной, а буква «pi» может использоваться для обозначения числа пи.

Кроме того, значки могут иметь специальные значения в математике. Например, знак «!» может использоваться для обозначения факториала числа, а знак «^» может использоваться для обозначения возведения числа в степень.

Использование значков в математике позволяет более точно и ясно выражать математические идеи и операции. Значки помогают упростить запись и понимание математических выражений.

Значение значка в математике: важность при чтении формул

Значки в математике играют важную роль при чтении и понимании формул. Каждый математический символ имеет свое значение и выполняет определенную функцию в выражении или уравнении. Правильное использование значков позволяет математикам ясно и точно выражать свои мысли и идеи.

Когда мы видим математическую формулу, значки в ней работают вместе, чтобы передать определенное значение или смысл. Например, символ «x» в уравнении может представлять неизвестное значение, которое мы хотим найти. Символ «y» может представлять зависимую переменную, а «+», «-«, «*», «/» и другие математические операторы указывают на выполняемые действия.

Значки в математике также могут указывать на специфические свойства или отношения между числами или переменными. Например, символ «≠» означает «не равно», а символ «≥» означает «больше или равно». Значки могут быть использованы для обозначения специальных функций, таких как квадратный корень (√), синус (sin), косинус (cos), и многое другое.

Кроме того, значки в математике могут быть объединены в формулы и уравнения, которые позволяют нам решать сложные математические задачи. Чтение и понимание этих формул требует знания значения каждого значка и его роли в контексте формулы. Например, в уравнении «x + 2 = 5», мы знаем, что символ «+» обозначает сложение, а символ «=» обозначает равенство.

Важно помнить, что значки в математике обладают строгими правилами использования и значения. Неправильное использование значков может привести к неправильным результатам или непониманию формулы. Поэтому, при чтении и понимании математических формул необходимо быть внимательным и точным в использовании значков и их значений.

Значение значка в математике: использование в уравнениях

Значки в математике играют важную роль и используются для обозначения различных математических операций и понятий. Они помогают нам записывать и понимать уравнения, формулы и выражения.

Один из наиболее распространенных значков в математике — знак равенства (=). Этот значок используется для обозначения равенства двух математических выражений. Например, уравнение «2 + 3 = 5» означает, что сумма двух чисел 2 и 3 равна числу 5.

Значок плюса (+) используется для обозначения сложения двух чисел или выражений. Например, «2 + 3» обозначает сложение чисел 2 и 3, что дает результат 5.

Значок минуса (-) используется для обозначения вычитания или разности двух чисел или выражений. Например, «5 — 2» обозначает разность чисел 5 и 2, что дает результат 3.

Значок умножения (×) используется для обозначения умножения двух чисел или выражений. Например, «3 × 4» обозначает умножение чисел 3 и 4, что дает результат 12.

Значок деления (÷) используется для обозначения деления одного числа или выражения на другое. Например, «10 ÷ 2» обозначает деление числа 10 на 2, что дает результат 5.

Значок деления нацело (÷) используется для обозначения целочисленного деления одного числа или выражения на другое. Например, «10 ÷ 3» означает, что при делении числа 10 на 3 получится результат 3 без остатка.

Значок процента (%) используется для обозначения процентного значения или доли числа. Например, «50%» обозначает половину числа, а «25% от 100» означает четверть числа 100.

Значок корня (√) используется для обозначения извлечения квадратного корня из числа. Например, «√16» обозначает извлечение квадратного корня из числа 16, что дает результат 4.

Это лишь некоторые из значков, используемых в математике. Их правильное понимание и использование позволяет нам записывать и решать уравнения, проводить математические операции и доказывать математические теоремы.

Значение значка в математике: связь с операциями

Значки в математике имеют особое значение и связаны с определенными операциями. Знаки помогают нам записывать и выражать различные математические операции и отношения между числами.

Одним из основных значков в математике является знак «плюс» (+). Этот знак обозначает операцию сложения. Например, 2 + 3 = 5, что означает, что если сложить числа 2 и 3, получится число 5.

Вторым важным значком является знак «минус» (-). Он обозначает операцию вычитания. Например, 5 — 2 = 3, что означает, что если вычесть из числа 5 число 2, получится число 3.

Еще одним значимым знаком является знак «умножить» (×). Он обозначает операцию умножения. Например, 2 × 3 = 6, что означает, что если умножить число 2 на число 3, получится число 6.

Знак «делить» (÷) обозначает операцию деления. Например, 6 ÷ 2 = 3, что означает, что если разделить число 6 на число 2, получится число 3.

Также существуют другие значки, которые обозначают другие математические операции, такие как возведение в степень (^), извлечение корня (√) и др. Используя эти значки, мы можем записывать и решать сложные математические задачи и формулы.

Знание значений и связи значков с операциями помогает нам лучше понимать и использовать математические концепции и решать различные задачи в нашей повседневной жизни.

ЗначокОписаниеПримеры

+	Сложение	2 + 3 = 5
—	Вычитание	5 — 2 = 3
×	Умножение	2 × 3 = 6
÷	Деление	6 ÷ 2 = 3

Значение значка в математике: примеры в различных областях

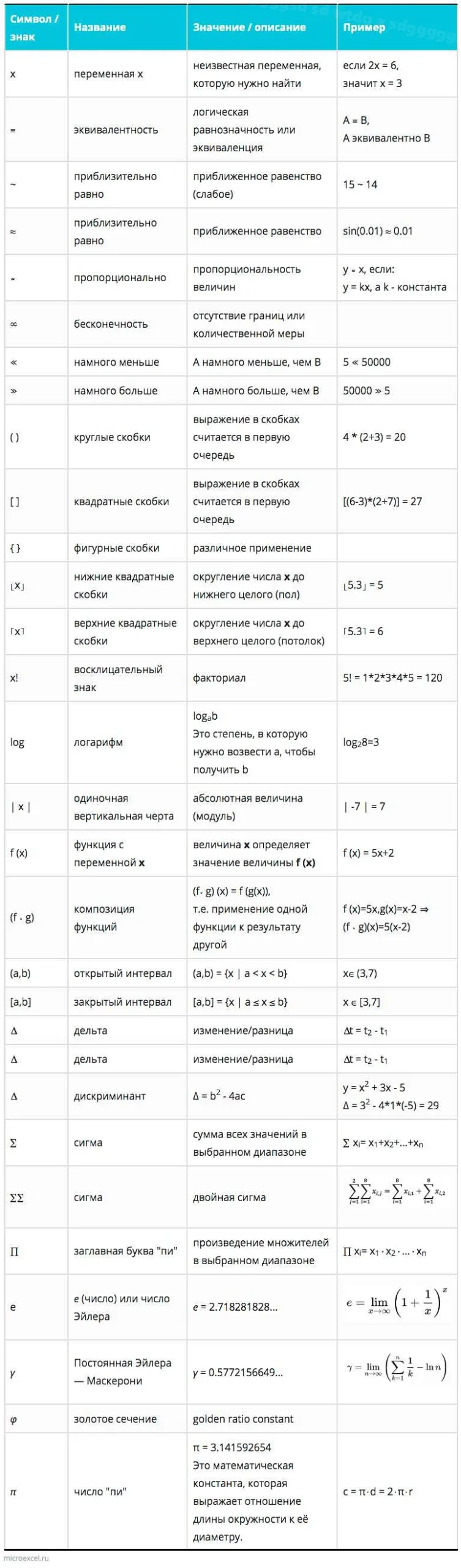
Математические значки играют важную роль в различных областях математики и науки в целом. Они помогают представить и объяснить сложные концепции, а также упрощают вычисления и решение задач. Ниже приведены некоторые примеры наиболее распространенных значков, которые встречаются в различных областях математики:

• ∑ (сигма) — символ суммы. Он используется для обозначения суммы последовательности чисел или выражений. Например, ∑(i=1 to n) i обозначает сумму всех чисел от 1 до n (1+2+3+…+n).
• ∫ (интеграл) — символ интеграла. Он используется в математическом анализе для обозначения интеграла функции. Например, ∫f(x)dx обозначает интеграл функции f(x) по переменной x.
• π (пи) — математическая константа, которая представляет отношение длины окружности к ее диаметру. Она используется в геометрии и тригонометрии для вычисления площадей и объемов.
• ≈ (примерно равно) — символ, который обозначает, что два числа или выражения примерно равны друг другу. Он используется для округления чисел или выражений до определенного числа знаков после запятой.
• √ (корень) — символ квадратного корня. Он используется для обозначения извлечения квадратного корня из числа или выражения.
• ∠ (угол) — символ угла. Он используется в геометрии для обозначения угла между двумя линиями или плоскостями.

Это лишь некоторые примеры значков, которые используются в математике. В каждой области математики существуют свои уникальные значки, которые помогают упростить и понять сложные концепции. Надеемся, что эти примеры помогут вам лучше понять роль значков в математике и их применение в различных областях.

Значение значка в математике: символы и их интерпретация

Математика использует широкий спектр символов для обозначения различных математических понятий. Каждый символ имеет своё уникальное значение и интерпретацию в контексте математических операций и формул.

Ниже приведены некоторые из наиболее распространенных символов и их интерпретация:

• + (плюс) – обозначает сложение двух или более чисел. Например, 2 + 3 = 5.
• — (минус) – обозначает вычитание одного числа из другого. Например, 5 — 3 = 2.
• * (звездочка) или x (латинская буква «x») – обозначают умножение двух или более чисел. Например, 2 * 3 = 6.
• / (деление) или : (двоеточие) – обозначают деление одного числа на другое. Например, 6 / 2 = 3.
• = (равно) – обозначает равенство двух выражений. Например, 2 + 3 = 5.
• < (меньше) – обозначает, что одно число меньше другого. Например, 2 < 3.
• > (больше) – обозначает, что одно число больше другого. Например, 3 > 2.

Это лишь несколько примеров символов и их значения в математике. Символы в математике играют важную роль в обозначении и описании различных математических операций и концепций. Понимание значения и интерпретации этих символов помогает в понимании и решении математических задач.

Значение значка в математике: важность для понимания концепций

Одним из основных значков в математике является знак равенства (=), который обозначает, что два выражения равны друг другу. Он позволяет нам сравнивать и связывать различные математические объекты.

Еще одним важным значком является плюс (+), который обозначает операцию сложения. Он используется для объединения двух или более чисел или выражений в одно.

Минус (-) обозначает операцию вычитания и используется для вычитания одного числа или выражения из другого.

Значок умножения (×) обозначает операцию умножения и используется для умножения двух или более чисел или выражений.

Значок деления (÷) обозначает операцию деления и используется для деления одного числа или выражения на другое.

Значки в математике также используются для обозначения различных функций и операций, таких как степень (^) для возведения в степень и корень (√) для извлечения квадратного корня.

Понимание значений и использование значков в математике помогает нам более глубоко понять различные концепции и операции. Они являются основой для построения математических моделей и решения различных задач.

Использование значков также помогает установить ясные и точные коммуникационные линии между математическими идеями и позволяет математикам обмениваться информацией и результатами своих исследований.

Важно понимать значения и использование значков в математике, чтобы быть успешным и эффективным в области математики и ее приложений.

Видео по теме:

Что такое значок в математике?

Значок в математике — это символ или знак, который используется для представления определенной операции или отношения между числами и объектами. Например, знак «+» используется для обозначения сложения, знак «-» — для вычитания, знак «*» — для умножения и т.д.

Какие основные значки используются в математике?

В математике используются различные значки для обозначения разных операций и отношений. Некоторые из основных значков включают знаки «+», «-«, «*», «/», «=», «>», »

Зачем нужны значки в математике?

Значки в математике необходимы для обозначения операций и отношений между числами и объектами. Они помогают нам записывать и понимать математические выражения и уравнения. Кроме того, значки позволяют нам выполнять вычисления и решать математические задачи.

Как помогают значки в решении математических задач?

Значки в решении математических задач играют важную роль. Они позволяют нам записывать и анализировать информацию, проводить необходимые вычисления и извлекать нужные выводы. Значки помогают нам формулировать и решать уравнения, неравенства и другие математические проблемы. Они также помогают нам понять отношения между числами и объектами.

Что такое значок в математике?

Значок в математике — это символ или знак, который используется для обозначения определенной математической операции, свойства или отношения.

Какие примеры значков в математике?

Примеры значков в математике включают знаки операций, такие как плюс (+), минус (-), умножить (×) и разделить (÷), а также символы для отношений, например, равно (=), больше (>), меньше (