Что значит знак дельта в математике

Знак дельта в математике обозначает разность между двумя значениями или изменение величины. Узнайте, как использовать знак дельта и его значение в математических вычислениях и уравнениях.

Знак дельта — один из наиболее широко используемых символов в математике, который обозначает изменение или разность между двумя величинами. В греческом алфавите дельта обозначает букву «D» и имеет форму треугольника. В математике этот символ широко используется для обозначения разности, приращения, изменения и дифференциала.

Основные свойства знака дельта позволяют упростить и удобно представить различные математические операции. Во-первых, дельта обозначает разность между двумя значениями, например, между начальным и конечным значением величины. Во-вторых, дельта используется для обозначения приращения, то есть изменения величины в течение определенного времени или интервала. В-третьих, дельта может быть использована для обозначения дифференциала — малой части изменения величины.

Применение знака дельта находится во многих различных областях математики и физики. В алгебре дельта используется для обозначения разности между двумя значениями или переменными. В дифференциальном исчислении дельта используется для обозначения малого изменения или дифференциала величины. В физике дельта может обозначать разность или приращение значений физических величин, таких как скорость или ускорение. В экономике дельта может использоваться для обозначения изменения цены, спроса или предложения.

Итак, знак дельта является важным символом в математике, который обозначает изменение или разность между двумя величинами. Он имеет много основных свойств и широкий спектр применений в различных областях науки и практической деятельности. Понимание и использование знака дельта помогает более точно и удобно представлять и анализировать различные процессы и явления.

Основные свойства и применение знака дельта в математике

Знак дельта (Δ) широко используется в математике и имеет несколько основных свойств и применений. Вот некоторые из них:

1. Δ используется для обозначения разности или изменения некоторой величины. Например, если у нас есть два числа a и b, то a — b может быть обозначено как Δ.
2. Δ также используется для обозначения дискриминанта в квадратном уравнении. Дискриминант позволяет определить, сколько корней имеет уравнение и какие они. Формула для вычисления дискриминанта выглядит следующим образом: Δ = b^2 — 4ac, где a, b и c — коэффициенты уравнения.
3. В математической статистике Δ может представлять разность между ожидаемыми и наблюдаемыми значениями. Например, если мы имеем две выборки данных и хотим сравнить их, мы можем вычислить Δ и использовать его для определения статистической значимости различий между ними.
4. Δ может также обозначать приращение некоторой функции. Например, если у нас есть функция f(x) и мы хотим вычислить изменение f(x) при изменении аргумента x на некоторое значение Δx, то мы можем записать это как f(x + Δx) — f(x).

Это лишь некоторые из основных свойств и применений знака дельта в математике. Он активно используется в различных областях математики, физики, статистики и других наук, где требуется обозначить разность или изменение величин.

Видео по теме:

Знак дельта: определение и происхождение

Символ Δ введен в математику в древности и происходит от буквы дельта греческого алфавита. Эта буква была часто использована в античной математике для обозначения изменения или разницы. Со временем знак дельта стал символизировать конкретные математические понятия и операции, связанные с изменениями, различиями или дельтами.

В современной математике знак дельта используется для обозначения разностей, изменений или приращений различных величин. Он может обозначать разницу между значениями функции в двух точках, изменение величины во времени или после некоторого события, а также другие подобные концепции.

Знак дельта имеет несколько свойств и правил, которые позволяют его использовать в математических выражениях и уравнениях. Он также нашел применение в других науках, таких как физика, химия, экономика и другие, где используется для обозначения изменений или разностей величин.

Знак дельта в алгебре: основные операции

Одной из основных операций, которая обозначается знаком дельта, является разность. Если у нас есть два числа a и b, то разность между ними можно обозначить следующим образом: Δ = a — b. Таким образом, знак дельта показывает, что мы вычитаем одно число из другого.

Знак дельта также используется для обозначения изменения или приращения величины. Например, если у нас есть начальное значение x и конечное значение y, то изменение этой величины можно записать как Δx = y — x. Здесь знак дельта показывает, что мы вычисляем разницу между конечным и начальным значением.

Кроме того, знак дельта используется для обозначения дискриминанта в квадратном уравнении. Дискриминант определяет количество и характер корней квадратного уравнения и вычисляется по формуле Δ = b^2 — 4ac, где a, b и c — коэффициенты уравнения.

Также знак дельта может использоваться для обозначения набора или совокупности в математике. Например, Δ = {x | x > 0} означает множество всех чисел x, которые больше нуля.

В заключение, знак дельта в алгебре играет важную роль и обозначает различные операции и свойства. Он позволяет выполнять вычисления и решать разнообразные задачи, связанные с алгеброй и математикой в целом.

Вопрос-ответ:

Зачем нужен знак дельта в математике?

Знак дельта в математике используется для обозначения разности между двумя величинами или изменения значения величины. Он помогает нам измерять и анализировать различия и изменения в математических моделях и уравнениях.

Каким образом применяется знак дельта в математике?

Знак дельта может быть использован для обозначения разности между двумя величинами, например: Δx = x2 — x1. Он также может быть использован для обозначения изменения значения величины, например: Δy = y2 — y1. Также знак дельта может быть использован в различных математических формулах и уравнениях.

Какие свойства имеет знак дельта в математике?

Знак дельта обладает несколькими свойствами. Во-первых, он является линейным оператором, то есть он сохраняет линейность операций. Во-вторых, знак дельта обладает свойством коммутативности, то есть порядок операций не влияет на результат. Кроме того, знак дельта может быть применен как к числам, так и к векторам и матрицам.

Какие примеры применения знака дельта в математике?

Применение знака дельта в математике может быть разнообразным. Одним из примеров является использование знака дельта для измерения разности между двумя числами или величинами. Например, мы можем вычислить разность между текущим и предыдущим значением температуры с помощью знака дельта. Еще одним примером является использование знака дельта для измерения изменения значения функции в математических уравнениях.

Знак дельта в геометрии: связь с площадью и объемом

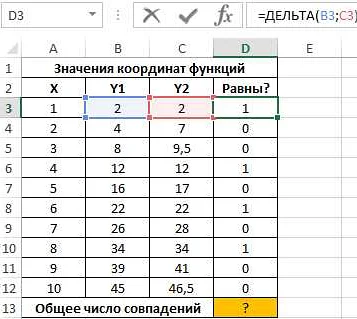
Знак дельта (Δ) в геометрии используется для обозначения площади треугольника или объема тела. Этот символ широко применяется в различных математических выражениях и формулах, связанных с геометрией.

Когда мы говорим о площади треугольника, знак дельта обычно используется для обозначения вычисляемой площади. Например, если у нас есть треугольник ABC, то его площадь может быть обозначена как SΔABC. Площадь треугольника можно вычислить, зная длины его сторон или длины сторон и угол между ними.

В случае с объемом тела, знак дельта также используется для обозначения вычисляемого объема. Например, если у нас есть параллелепипед с длиной a, шириной b и высотой c, то его объем может быть обозначен как VΔABC. Объем тела можно вычислить, зная его геометрические размеры.

Знак дельта играет важную роль в геометрии, помогая обозначить площадь треугольника или объем тела. Этот символ позволяет удобно записывать математические формулы и выражения, связанные с геометрией, и упрощает их понимание и восприятие.

Знак дельта в дифференциальном исчислении: производная и интеграл

Знак дельта (Δ) в математике используется для обозначения разницы или изменения величин. В дифференциальном исчислении знак дельта играет важную роль при определении производной и интеграла.

При рассмотрении производной, знак дельта используется для обозначения бесконечно малой разницы между значениями функции. Производная функции f(x) в точке x0 определяется как предел отношения изменения функции (Δf) к изменению аргумента (Δx), когда Δx стремится к нулю:

ΔxΔfΔf/Δx

x1 — x0	f(x1) — f(x0)	(f(x1) — f(x0)) / (x1 — x0)
x2 — x0	f(x2) — f(x0)	(f(x2) — f(x0)) / (x2 — x0)
…	…	…

Знак дельта (Δ) в производной помогает нам понять, как функция меняется при изменении аргумента и является ключевым понятием в дифференциальном исчислении.

При рассмотрении интеграла, знак дельта используется для обозначения бесконечно малого приращения аргумента. Интеграл функции f(x) от a до b определяется как предел суммы площадей бесконечно малых прямоугольников, где ширина каждого прямоугольника стремится к нулю:

Δxf(x)Δx * f(x)

x1 — x0	f(x0)	(x1 — x0) * f(x0)
x2 — x1	f(x1)	(x2 — x1) * f(x1)
…	…	…

Знак дельта (Δ) в интеграле помогает нам понять, как функция распределена на заданном интервале и является важной составляющей интегрального исчисления.

Использование знака дельта в дифференциальном исчислении позволяет нам более точно анализировать функции и их изменения. Именно благодаря знаку дельта мы можем определить производную и интеграл функции и применять их в различных областях науки и техники.

Знак дельта в теории вероятностей: вероятность и случайные величины

В теории вероятностей знак дельта (Δ) используется для обозначения разности между двумя случайными величинами. Вероятность разности между двумя случайными величинами может быть вычислена с использованием этого знака.

Одним из основных применений знака дельта в теории вероятностей является вычисление вероятности разности случайных величин. Для этого используется функция распределения разности (delta function), которая позволяет вычислить вероятность того, что разность двух случайных величин примет определенное значение.

Знак дельта также может использоваться для обозначения оператора разности в математических выражениях. Он может быть применен к функциям распределения и плотностям вероятности, чтобы указать на разность между двумя случайными величинами.

В теории вероятностей знак дельта играет важную роль в анализе случайных величин и вычислении их характеристик. Он позволяет определить вероятность разности между двумя случайными величинами, что помогает в решении различных задач, связанных с вероятностным анализом.

Использование знака дельта в теории вероятностей помогает упростить вычисления и обозначения, особенно при работе с различными случайными величинами. Это позволяет более эффективно анализировать и предсказывать случайные события и их вероятности.

Знак дельта в физике: изменение и производные величин

Знак дельта (Δ) в физике широко используется для обозначения изменения и производных величин. Этот символ позволяет выразить разницу между начальным и конечным значениями физической величины или изменение этой величины во времени.

Один из основных способов использования знака дельта в физике – обозначение приращения. Если физическая величина обозначается буквой, например, x, то изменение этой величины может быть выражено как Δx. Такое обозначение показывает, насколько изменилась величина x от начального значения до конечного. Например, если начальное значение x равно 10, а конечное – 15, то изменение величины x составит Δx = 15 — 10 = 5.

Кроме того, знак дельта может использоваться для обозначения производных величин. Например, скорость может быть обозначена как v, а изменение этой величины во времени – как Δv. Такое обозначение позволяет выразить разницу между начальной и конечной скоростью или изменение скорости во времени. Аналогично, ускорение может быть обозначено как a, а изменение ускорения во времени – как Δa.

Таким образом, знак дельта является важным инструментом в физике для обозначения изменения и производных величин. Он позволяет выразить разницу между начальным и конечным значениями физической величины или изменение этой величины во времени, что является основой для проведения анализа и решения задач в физике.

Знак дельта в компьютерных науках: алгоритмы и оптимизация

Знак дельта, обозначаемый символом Δ, имеет важное значение в компьютерных науках, особенно в области алгоритмов и оптимизации. Он используется для обозначения разности или изменения каких-либо величин или состояний.

В алгоритмах знак дельта широко применяется для вычисления и сравнения изменений во времени выполнения программы. Он позволяет определить, насколько эффективно работает алгоритм и какие улучшения могут быть внесены для оптимизации производительности.

Оптимизация является важным аспектом компьютерных наук, и знак дельта играет значительную роль в этом процессе. Он используется для измерения и сравнения различных параметров, таких как время выполнения, объем памяти или энергопотребление, для определения оптимальных параметров или алгоритмов.

Важно отметить, что знак дельта также используется в других областях компьютерных наук, таких как машинное обучение и статистика. Он может быть применен для оценки изменений в данных или моделях и анализа их статистической значимости.

Таким образом, знак дельта играет важную роль в компьютерных науках, особенно в области алгоритмов и оптимизации. Он позволяет измерить и сравнить изменения, а также определить эффективность и оптимальность различных параметров или алгоритмов.

Знак дельта в экономике: изменение и вариации показателей

В экономике знак дельта обычно используется для обозначения изменения или вариации показателей. Дельта-значение позволяет измерить разницу между двумя показателями или указать на изменение показателя во времени.

Дельта-значение может быть положительным, отражая рост показателя, или отрицательным, указывая на его снижение. Это позволяет анализировать динамику экономических показателей, идентифицировать тренды и оценивать эффективность различных стратегий и политик.

Применение знака дельта в экономике широко распространено. Он используется в финансовой аналитике для оценки изменения стоимости активов, доходности инвестиций и финансовых показателей компаний. Также дельта-значение применяется в макроэкономическом анализе для измерения изменения уровня инфляции, безработицы, ВВП и других важных экономических показателей.

Знак дельта в экономике является мощным инструментом для исследования динамики и изменения показателей. Он позволяет выявить тренды и установить причины изменений в экономической ситуации. Поэтому понимание и использование знака дельта в экономике является неотъемлемой частью анализа и прогнозирования экономических процессов.