Что этот знак обозначает в математике

Эта статья рассказывает о значении и использовании определенного знака в математике. Узнайте, каким образом этот знак применяется для обозначения конкретных математических операций и свойств, и как он может быть использован в различных математических формулах и уравнениях.

Математика — это наука, которая изучает числа, формулы, связи и паттерны, используемые для измерения и описания физических явлений. В математике, знаки играют важную роль в обозначении операций и отношений между числами и объектами. Каждый знак имеет своё специальное значение и используется для передачи определённой информации.

Один из самых известных знаков в математике — это знак равенства (=). Он используется для обозначения равенства двух выражений или чисел. Например, выражение «2+2=4» означает, что сумма двух чисел 2 равна числу 4. Знак равенства является основным знаком в математике и основой для решения уравнений и задач.

Если знак равенства — это основной знак математики, то знаки операций с числами (сложение, вычитание, умножение, деление) — это основные инструменты математического анализа и решения задач. Каждый знак операции имеет своё значение и используется для выполнения определённой математической операции.

Знаки операций являются ключевыми для арифметики, алгебры и других разделов математики. Например, знак сложения (+) используется для обозначения операции сложения двух чисел. Знак вычитания (-) используется для обозначения операции вычитания одного числа из другого. Знак умножения (*) используется для обозначения операции умножения двух чисел. Знак деления (/) используется для обозначения операции деления одного числа на другое. Знание этих знаков позволяет выполнять различные математические операции и решать сложные задачи.

Символы в математике: важность понимания

Символы в математике могут представлять операции, такие как сложение (+), вычитание (-), умножение (×) и деление (÷). Они также могут обозначать отношения, такие как равенство (=), больше (>), меньше (

Понимание этих символов позволяет математикам записывать и решать уравнения, формулировать и доказывать теоремы, анализировать и интерпретировать данные и многое другое. Они также позволяют общаться и передавать математические идеи и концепции другим людям.

Ошибки в понимании и использовании математических символов могут привести к неправильным результатам и непониманию математических концепций. Поэтому важно уделить внимание изучению и пониманию этих символов, чтобы быть успешным в математике и других научных областях, где они используются.

В заключение, знание и понимание символов в математике является неотъемлемой частью успешного изучения и применения математических концепций. Они позволяют нам записывать и решать уравнения, формулировать и доказывать теоремы и общаться математическими идеями. Поэтому необходимо уделить время и усилия, чтобы узнать и понять основные символы и их значения в математике.

Знак «плюс»: основная операция сложения

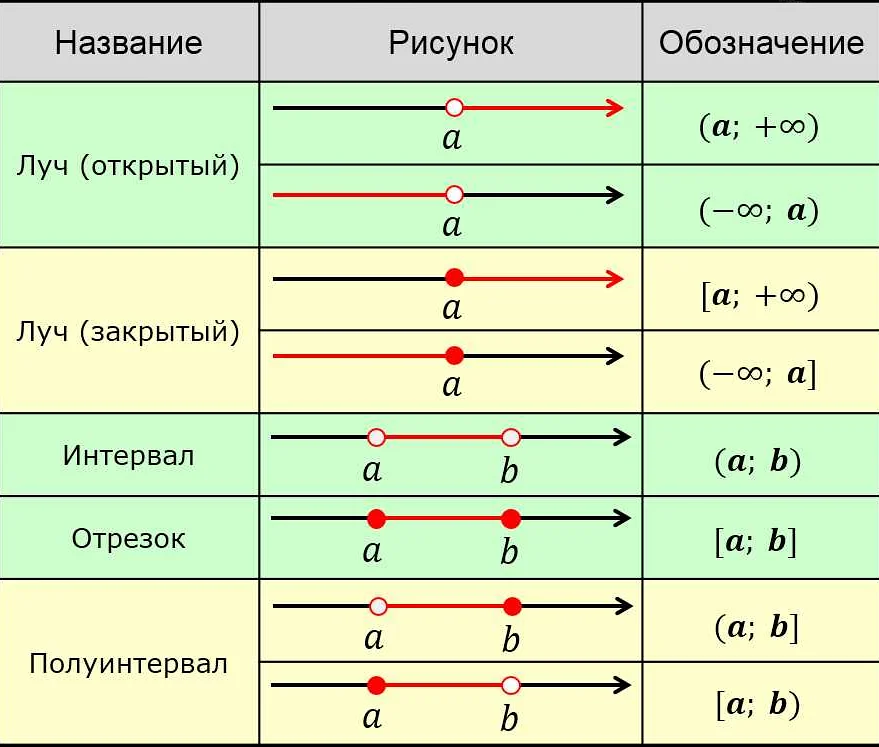
Знак «плюс» используется в математических выражениях для обозначения сложения чисел. Например, выражение 2 + 3 означает, что необходимо сложить числа 2 и 3, что в итоге даст сумму 5.

Числа, которые складываются, называются слагаемыми, а результат сложения — суммой. Например, в выражении 2 + 3, числа 2 и 3 являются слагаемыми, а сумма равна 5.

Операция сложения имеет несколько основных свойств:

СвойствоОписаниеПример

Коммутативность	Порядок слагаемых не влияет на результат сложения	2 + 3 = 3 + 2 = 5
Ассоциативность	Порядок скобок не влияет на результат сложения трех или более чисел	(2 + 3) + 4 = 2 + (3 + 4) = 9
Нейтральный элемент	Сумма числа и нуля равна этому числу	2 + 0 = 2
Обратный элемент	Сумма числа и его обратного равна нулю	2 + (-2) = 0

Знак «плюс» также используется в математических выражениях для обозначения положительных чисел. Например, число 5 можно записать как +5, чтобы подчеркнуть его положительность.

Важно отметить, что знак «плюс» имеет другие значения и применения за пределами операции сложения в математике. Например, он может использоваться для обозначения положительных зарядов в физике или положительных чисел в программировании.

Знак «минус»: операция вычитания и отрицательные числа

Операция вычитания выполняется следующим образом: первое число, из которого вычитают, называется уменьшаемым, а второе число, которое вычитают, называется вычитаемым. Результатом операции вычитания является разность между этими двумя числами.

Знак «минус» также используется для обозначения отрицательных чисел. Отрицательное число принято записывать с помощью знака «минус» перед числом. Например, число -5 означает, что на числовой оси данное число находится слева от нуля и имеет величину 5.

Отрицательные числа позволяют работать с долгами, температурой ниже нуля, отрицательными изменениями и другими ситуациями, где необходимо учитывать отрицательные значения. Они играют важную роль в математике и её приложениях.

Знак «умножить»: операция умножения и таблица умножения

Символ «умножить» выглядит как крестик (×) и обычно помещается между множителями. Например, выражение 2 × 3 означает, что число 2 умножается на число 3.

Операция умножения имеет несколько свойств, таких как коммутативность (порядок множителей не важен), ассоциативность (порядок выполнения умножения не важен) и дистрибутивность (умножение распространяется на сложение и вычитание).

Для облегчения запоминания результатов умножения, часто используется таблица умножения. Таблица умножения представляет собой матрицу, в которой значения произведений всех чисел от 1 до 10 записаны в ячейки таблицы.

Пример таблицы умножения:

• 1 х 1 = 1
• 1 х 2 = 2
• 1 х 3 = 3
• …
• 10 х 9 = 90
• 10 х 10 = 100

Таблица умножения помогает ученикам запомнить результаты умножения и быстро выполнять умножение чисел в уме. Она также является полезным инструментом для решения математических задач и составления таблиц и графиков.

Знак «разделить»: операция деления и десятичные дроби

В математике знак «разделить», обозначаемый символом «/», используется для обозначения операции деления. Операция деления позволяет разделить одно число на другое и найти результат этого разделения.

Например, если у нас есть числа 10 и 2, то запись «10 / 2» означает, что мы делим число 10 на число 2. Результатом этого деления будет число 5.

Десятичные дроби также могут быть представлены с использованием знака «разделить». Например, число 0,5 можно записать как «1 / 2», что означает, что число 1 разделено на число 2.

Знак «разделить» также может использоваться в комбинации с другими математическими символами. Например, если мы хотим выразить отношение двух величин, мы можем использовать знак «разделить» в формате «a / b», где «a» и «b» — числа или выражения. Это позволяет нам указать, что «a» разделено на «b» или что «a» составляет долю от «b».

Важно отметить, что операция деления может иметь ограничения, например, деление на ноль. Деление на ноль неопределено в математике и не имеет смысла.

Знак «равно»: сравнение и уравнения

В математике знак «равно» (=) используется для сравнения двух выражений или для записи уравнений.

Когда мы сравниваем два выражения, знак «равно» показывает, что эти выражения имеют одинаковое значение. Например, 2 + 3 = 5 означает, что сумма чисел 2 и 3 равна 5.

Знак «равно» также используется для записи уравнений, которые содержат одну или несколько переменных. Уравнение — это математическое выражение, в котором две стороны соединены знаком «равно». Решение уравнения состоит в нахождении значений переменных, при которых обе его стороны становятся равными.

Например, x + 5 = 10 — это уравнение, которое говорит нам, что сумма переменной x и числа 5 равна числу 10. Для решения этого уравнения мы должны найти значение переменной x, при котором данное равенство выполняется. В данном случае, значение переменной x равно 5.

Знак «равно» играет важную роль в математике, так как он позволяет сравнивать и связывать различные математические объекты. Он является основой для доказательств и решений уравнений, что делает его одним из ключевых символов в математической нотации.

Видео по теме:

Вопрос-ответ:

Что означает знак «+» в математике?

Знак «+» в математике обозначает операцию сложения. Он используется для того, чтобы указать, что нужно складывать два или более числа. Например, если написать 2 + 3, это значит, что нужно сложить числа 2 и 3, и результатом будет число 5.

Зачем нужен знак «-» в математике?

Знак «-» в математике обозначает операцию вычитания. Он используется для того, чтобы вычесть одно число из другого. Например, если написать 5 — 3, это значит, что нужно вычесть число 3 из числа 5, и результатом будет число 2.

Какое значение имеет знак «×» в математике?

Знак «×» в математике обозначает операцию умножения. Он используется для того, чтобы указать, что нужно умножить два или более числа. Например, если написать 2 × 3, это значит, что нужно умножить числа 2 и 3, и результатом будет число 6.

Что означает знак «÷» в математике?

Знак «÷» в математике обозначает операцию деления. Он используется для того, чтобы разделить одно число на другое. Например, если написать 6 ÷ 3, это значит, что нужно поделить число 6 на число 3, и результатом будет число 2.

Какое значение имеет знак «=» в математике?

Знак «=» в математике обозначает равенство. Он используется для того, чтобы указать, что два выражения или значения равны друг другу. Например, если написать 2 + 3 = 5, это значит, что выражение «2 + 3» равно значению «5».

Зачем нужны знаки в математике?

Знаки в математике играют важную роль, они помогают нам записывать и понимать различные математические операции и отношения. Они позволяют нам выражать и передавать информацию более точно и компактно.

Какие знаки используются в математике?

В математике используется большое количество различных знаков. Некоторые из самых распространенных знаков включают плюс (+), минус (-), умножить (×), делить (÷), равно (=), больше (>), меньше (

Знак «больше» и «меньше»: неравенства и сравнение чисел

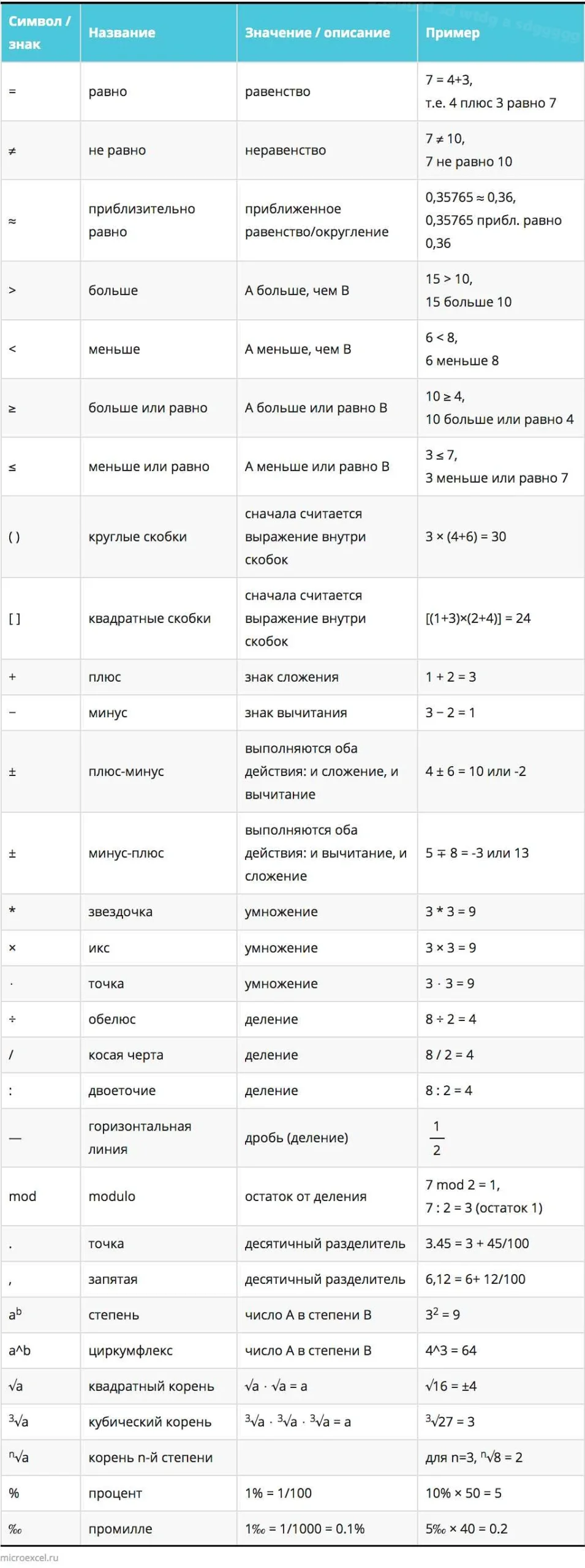
Если число a больше числа b, то можно записать неравенство a > b. Например, 5 > 3 означает, что число 5 больше числа 3.

Аналогично, если число a меньше числа b, то можно записать неравенство a < b. Например, 2 < 7 означает, что число 2 меньше числа 7.

При использовании знаков «больше» и «меньше» в математических выражениях можно использовать также знаки равенства (≥ и ≤) для обозначения «больше или равно» и «меньше или равно». Например, 4 ≤ 4 означает, что число 4 меньше или равно числу 4.

Знаки «больше» и «меньше» позволяют сравнивать не только целые числа, но и дробные, отрицательные и даже бесконечные числа. Например, -1 < 0 означает, что число -1 меньше числа 0, а 1/2 > 1/4 означает, что дробь 1/2 больше дроби 1/4.

Важно помнить, что знаки «больше» и «меньше» указывают только на отношение между числами и не выполняют абсолютного сравнения. Например, из неравенства 3 > 2 не следует, что число 3 во всех случаях больше числа 2. Они лишь указывают на отношение в конкретном контексте.

Таким образом, знаки «больше» и «меньше» играют важную роль в математике, позволяя сравнивать числа и устанавливать отношения между ними.

Знак «скобки»: порядок операций и группировка чисел

Один из основных случаев использования скобок — изменение порядка операций. В математике существует определенный порядок выполнения операций, который называется «правилом умножения и деления перед сложением и вычитанием». Согласно этому правилу, умножение и деление выполняются раньше сложения и вычитания. Однако, с помощью скобок можно изменить этот порядок и указать, какие операции должны быть выполнены первыми.

Например, рассмотрим выражение 2 + 3 * 4. Согласно правилу умножения и деления перед сложением и вычитанием, сначала производится умножение 3 * 4, а затем сложение 2 + 12, что дает результат равный 14. Однако, если мы добавим скобки в данное выражение (2 + 3) * 4, то сначала будет выполнена операция внутри скобок 2 + 3, что дает результат равный 5, а затем произведение 5 * 4, что дает результат равный 20.

Второй случай использования скобок — группировка чисел. С помощью скобок можно указать, какие числа должны быть сгруппированы вместе и рассматриваться как единое целое.

Например, рассмотрим выражение 3 * (2 + 4). Скобки здесь группируют числа 2 и 4 и указывают, что их нужно сначала сложить. Таким образом, сначала будет выполнена операция внутри скобок 2 + 4, что дает результат равный 6, а затем произведение 3 * 6, что дает результат равный 18.

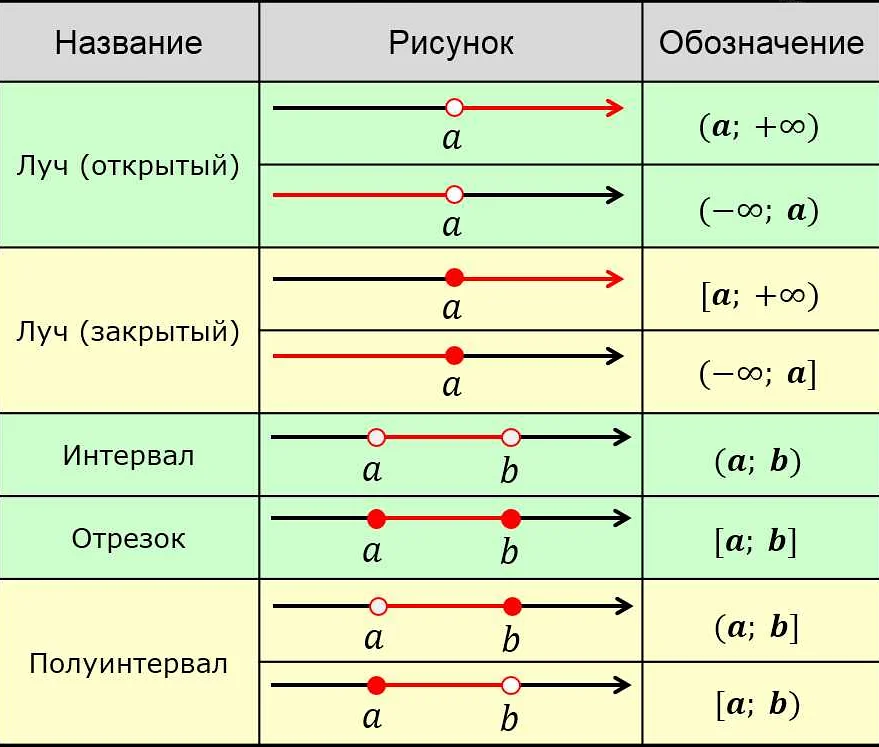
Важно знать, что в математике существуют различные типы скобок, такие как круглые скобки ( ), квадратные скобки [ ] и фигурные скобки { }. Каждый тип скобок имеет свои особенности и используется в определенных случаях. Например, круглые скобки обычно используются для обозначения приоритета операций и группировки чисел, квадратные скобки могут использоваться в матрицах или для обозначения интервалов, а фигурные скобки используются для обозначения множеств.

Тип скобокПример использования

Круглые скобки	(2 + 3) * 4
Квадратные скобки	[1, 2, 3]
Фигурные скобки	{x | x > 0}

В заключение, знак «скобки» в математике играет важную роль в определении порядка операций и группировки чисел. С помощью скобок можно изменить приоритет выполнения операций и указать, какие числа должны быть сгруппированы вместе. При использовании скобок важно учитывать правила математических операций и выбирать подходящий тип скобок для каждой конкретной ситуации.