Что является целью математической статистики

Цель математической статистики — разработка и применение математических методов для описания и анализа статистических данных. Она помогает исследователям выявлять закономерности, делать выводы на основе вероятностных моделей и принимать обоснованные решения на основе статистических данных.

Математическая статистика – это важная область математики, которая изучает методы сбора, анализа и интерпретации данных. Основная цель математической статистики заключается в выявлении закономерностей и моделей, скрытых в больших объемах данных, а также в принятии решений на основе этих данных.

Ключевыми аспектами математической статистики являются вероятностные распределения, выборочные методы и оценка параметров. Вероятностные распределения позволяют моделировать случайные явления, а выборочные методы позволяют изучать свойства выборок из генеральной совокупности. Оценка параметров позволяет определить значения неизвестных параметров на основе имеющихся данных.

Применение математической статистики находит широкое применение в различных областях, включая науку, экономику, социологию, медицину и технику. Например, математическая статистика используется для проведения опросов и исследований, анализа экономических данных, прогнозирования погоды, анализа медицинских данных и многое другое.

Использование математической статистики позволяет более объективно и точно изучать и анализировать данные, принимать взвешенные решения и предсказывать будущие события. Она помогает исследователям и специалистам находить скрытые закономерности и тенденции, основываясь на имеющихся данных, и принимать обоснованные решения на основе этих результатов.

Цель математической статистики

Одной из главных целей математической статистики является описание и интерпретация данных. Для этого статистики используют методы сбора, организации и анализа данных. С помощью этих методов можно выявить закономерности, связи и тренды в данных, а также оценить их достоверность и значимость.

Важной задачей математической статистики является построение статистических моделей для объяснения данных. С помощью моделей можно предсказывать поведение данных, исследовать влияние различных факторов и проверять гипотезы. Построение и использование статистических моделей позволяет принимать обоснованные решения на основе данных и сокращать риски ошибок и неправильных выводов.

Другой важной целью математической статистики является оценка неопределенности и рисков. Статистические методы позволяют оценить погрешности и доверительные интервалы для полученных результатов, что помогает принимать решения на основе уровня риска и надежности данных.

В целом, целью математической статистики является использование математических методов для анализа данных, построения моделей и принятия обоснованных решений на основе имеющихся данных. Она играет важную роль в различных областях, таких как экономика, медицина, социология, инженерия и другие, где требуется обработка и анализ данных для принятия важных решений.

Важность статистики в современном мире

Статистика играет ключевую роль в современном мире, она помогает нам понять и анализировать большие объемы данных. Статистика помогает нам принимать взвешенные решения на основе фактов и доказательств, а не на основе предположений или предубеждений.

Одним из важнейших аспектов статистики является ее применение в научных исследованиях. Статистический анализ позволяет установить закономерности и связи между различными явлениями, что является основой для формулирования новых гипотез и теорий. Благодаря статистике мы можем проверять гипотезы и делать выводы на основе наблюдений.

Статистика также играет важную роль в прогнозировании и планировании. Например, она помогает предсказать будущий спрос на товары и услуги, что позволяет компаниям принять решения о производстве и распределении ресурсов. Также статистика используется при разработке экономических моделей и прогнозировании экономической ситуации.

В современном мире большое значение приобретает анализ данных в различных областях, таких как маркетинг, медицина, социология и т.д. Статистика позволяет нам изучать и понимать поведение людей, прогнозировать рыночные тенденции и принимать управленческие решения на основе данных.

И наконец, статистика является неотъемлемой частью нашей повседневной жизни. Мы сталкиваемся с данными и статистикой везде – от новостей и политических обсуждений до спортсменов и развлекательной индустрии. Понимание статистики помогает нам проанализировать информацию и принимать осознанные решения.

Применение математической статистики в различных областях

Математическая статистика играет важную роль во многих областях науки, техники и социальных наук. Ее методы и инструменты широко используются для анализа данных, выявления закономерностей и принятия информированных решений. Ниже представлены несколько областей, в которых применение математической статистики имеет особое значение:

Медицина	Математическая статистика используется для анализа результатов клинических испытаний, оценки эффективности лекарственных препаратов, исследования эпидемиологических данных и моделирования заболеваемости. Она помогает выявлять факторы риска, проводить прогнозирование заболеваемости и оценивать качество медицинской помощи.
Финансы и экономика	В финансовой и экономической сферах математическая статистика применяется для анализа финансовых данных, моделирования цен на активы, прогнозирования финансовых рынков и оценки рисков. Она также играет важную роль в разработке статистических методов для оценки экономических показателей и макроэкономического анализа.
Инженерия и наука о материалах	В инженерии и науке о материалах математическая статистика используется для анализа результатов экспериментов, моделирования процессов и оптимизации производства. Она помогает оценивать качество и надежность изделий, прогнозировать и управлять рисками, а также проводить статистическое контролирование качества.
Социальные науки	В социальных науках математическая статистика используется для анализа социальных данных, изучения социальных явлений и прогнозирования социальных процессов. Она помогает выявлять тенденции, зависимости и взаимосвязи в обществе, а также оценивать социальные программы и политику.

Это лишь некоторые области, в которых математическая статистика применяется для анализа данных и принятия решений. Ее методы и подходы активно используются во многих других областях, таких как экология, телекоммуникации, геология, астрономия и другие.

Основные компоненты математической статистики

Основные компоненты математической статистики включают:

1. Выборка: выборка представляет собой подмножество данных, которые были собраны для исследования. Выборка может быть случайной или наблюдательной. Случайная выборка представляет собой случайно выбранные данные из генеральной совокупности, в то время как наблюдательная выборка состоит из данных, наблюдаемых или измеряемых исследователем.
2. Описательные статистики: описательные статистики используются для описания исследуемой выборки данных. Они включают такие характеристики, как среднее значение, медиана, дисперсия и другие.
3. Математические модели: математические модели используются для анализа данных и предсказания взаимосвязей между переменными. Они позволяют строить статистические модели, которые могут быть использованы для прогнозирования будущих событий или проверки гипотез.
4. Теория вероятности: теория вероятности является основой для математической статистики. Она позволяет оценивать вероятность того, что определенное событие произойдет, и использовать эту информацию для принятия статистических решений.
5. Статистические тесты: статистические тесты используются для проверки гипотез и определения, насколько результаты исследования статистически значимы. Они позволяют исследователям делать выводы на основе имеющихся данных и оценивать степень уверенности в этих выводах.

Основные компоненты математической статистики взаимосвязаны и позволяют исследователям получить достоверные и объективные результаты на основе данных. Их применение имеет важное значение для принятия решений в различных областях знаний и помогает понять закономерности в данных и решить ряд задач, связанных с прогнозированием, классификацией, оптимизацией и другими.

Сбор и обработка статистических данных

Сбор статистических данных включает в себя выборочное наблюдение за объектами или явлениями, измерение или фиксацию нужных характеристик и их запись. Для этого используются различные методы, такие как опросы, эксперименты или наблюдения.

Однако сбор данных может столкнуться с определенными проблемами, такими как ошибки наблюдения или сбора информации, несоответствие выбранной выборки популяции, а также проблемы соблюдения этических норм при проведении исследований.

Обработка статистических данных включает в себя анализ и интерпретацию полученной информации. Для этого используются различные методы статистики, такие как описательная статистика, статистический анализ и тестирование гипотез. Цель обработки данных заключается в выявлении паттернов, отношений и закономерностей, а также в проведении статистических выводов и прогнозировании.

Сбор и обработка статистических данных имеют широкое применение во многих областях, таких как наука, экономика, медицина, социология и маркетинг. Они помогают принимать взвешенные решения на основе фактических данных, а также предоставляют возможность оценивать эффективность и результаты различных процессов и действий.

Анализ и интерпретация статистических данных

На первом этапе анализа статистических данных выполняется их описательная статистика. В рамках этого этапа происходит вычисление таких показателей, как среднее значение, медиана, мода, дисперсия и стандартное отклонение. Эти показатели позволяют получить представление о центральных значениях, разбросе данных и форме их распределения.

Далее следует проведение корреляционного анализа, который позволяет определить степень связи между двумя или более переменными. Корреляция может быть положительной, отрицательной или незначительной. По результатам корреляционного анализа можно сделать выводы о наличии или отсутствии зависимостей между переменными.

Одним из основных методов анализа статистических данных является статистический тест. С его помощью можно проверить гипотезы о существовании различий между группами или о связи между переменными. Тестирование позволяет сделать статистически обоснованные выводы на основе имеющихся данных.

Интерпретация статистических данных заключается в объяснении полученных результатов и их применении в практической деятельности. На основе анализа и интерпретации данных можно принимать решения, разрабатывать стратегии и прогнозировать будущие события.

Все эти этапы анализа и интерпретации статистических данных позволяют извлекать информацию, делать выводы и принимать обоснованные решения. Математическая статистика является незаменимым инструментом в многих областях науки, бизнеса и социальной сферы, где требуется обработка и анализ больших объемов данных.

Прогнозирование на основе статистических данных

Для прогнозирования на основе статистических данных применяются различные методы и модели. Одним из основных инструментов является регрессионный анализ, который позволяет определить зависимость между независимыми и зависимыми переменными и использовать ее для прогнозирования.

Другим распространенным методом прогнозирования является временной ряд. Временной ряд представляет собой последовательность наблюдений, сделанных в разные моменты времени. Анализ временных рядов позволяет выявить тренды, цикличность и сезонность в данных и использовать их для прогнозирования будущих значений.

Прогнозирование на основе статистических данных широко применяется в различных областях, таких как экономика, финансы, маркетинг, медицина и другие. Например, на основе исторических данных о продажах компания может прогнозировать будущий спрос на свои товары, а биржевые трейдеры могут использовать статистические модели для предсказания цен на финансовых рынках.

Важным аспектом прогнозирования на основе статистических данных является оценка точности и надежности прогнозов. Для этого применяются различные методы, такие как кросс-валидация, анализ остатков и другие.

В целом, прогнозирование на основе статистических данных играет важную роль в принятии решений и планировании деятельности в различных сферах жизни и бизнеса. Оно позволяет прогнозировать будущие тенденции и повышать эффективность принимаемых решений.

Оценка достоверности и точности статистических выводов

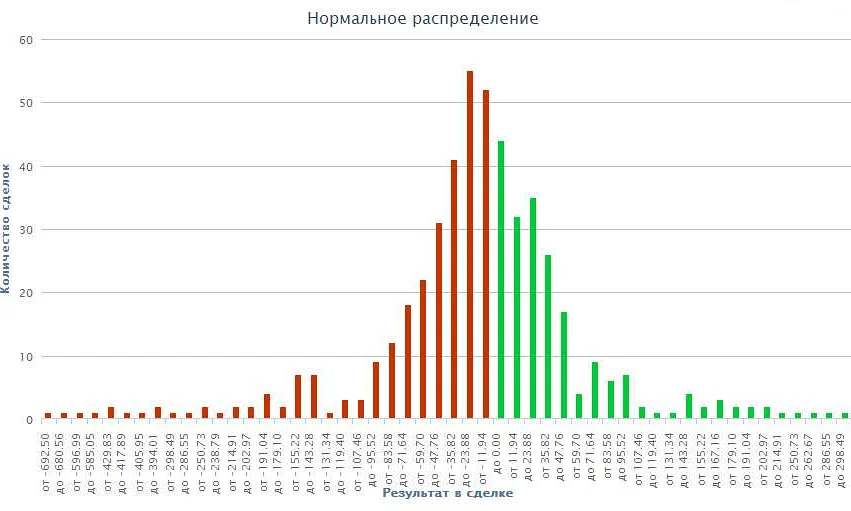
Оценка достоверности статистических выводов связана с проверкой статистических гипотез. При проверке гипотезы мы оцениваем вероятность того, что наблюдаемые данные могут быть объяснены случайностью. Для этого используется так называемый уровень значимости, который определяет, насколько нам нужно быть уверенными, чтобы отвергнуть нулевую гипотезу. Если вероятность того, что наблюдаемые данные могут быть объяснены случайностью, меньше уровня значимости, то мы отвергаем нулевую гипотезу в пользу альтернативной гипотезы.

Оценка точности статистических выводов связана с определением доверительных интервалов. Доверительный интервал – это интервал, который содержит оценку неизвестного параметра генеральной совокупности с определенной вероятностью. Чем больше доверительная вероятность, тем шире доверительный интервал. Оценка точности статистических выводов позволяет учитывать случайные флуктуации в данных и определять диапазон значений, в котором может находиться истинное значение параметра генеральной совокупности.

Важно отметить, что оценка достоверности и точности статистических выводов напрямую зависит от выбора статистических методов и моделей. Неправильный выбор метода или модели может привести к неверным или неточным результатам. Поэтому, при проведении статистического анализа данных, необходимо тщательно подходить к выбору методов и моделей и учитывать особенности и ограничения каждого из них.

Оценка достоверностиОценка точности

Проверка статистических гипотез	Определение доверительных интервалов
Уровень значимости	Доверительная вероятность
Отвержение нулевой гипотезы	Оценка случайных флуктуаций

Вопрос-ответ:

Какова цель математической статистики?

Цель математической статистики состоит в разработке методов и моделей для анализа данных и получения выводов о популяции на основе выборки. Она позволяет сделать выводы о характеристиках популяции на основе ограниченного количества данных.

В чем заключаются ключевые аспекты математической статистики?

Ключевые аспекты математической статистики включают сбор данных, их обработку и анализ, выбор моделей, проверку гипотез, оценку параметров и прогнозирование. Она также занимается изучением случайных явлений и разработкой статистических методов для работы с данными.

Какие методы используются в математической статистике?

В математической статистике используются различные методы, включая методы описательной статистики, методы статистического вывода, методы регрессионного анализа, методы анализа временных рядов и многие другие. Каждый метод имеет свои особенности и применяется в зависимости от конкретной задачи и данных.

Как математическая статистика применяется на практике?

Математическая статистика применяется в различных областях, таких как экономика, медицина, социология, финансы, инженерия и многие другие. Она используется для анализа данных, прогнозирования, принятия решений, проверки гипотез и многое другое. Например, она может помочь определить, какой продукт будет популярен на рынке, какой лечебный препарат эффективен, или какие факторы влияют на доходы компании.

Каким образом математическая статистика помогает в принятии решений?

Математическая статистика позволяет анализировать данные, делать выводы на основе этих данных и принимать обоснованные решения. Она помогает оценить вероятности различных событий, определить риски и прогнозировать результаты. Например, она может помочь банку определить, кому выдать кредит, основываясь на вероятности возврата долга, или помочь компании принять решение о внедрении нового продукта, основываясь на предсказании его популярности.

Зачем нужна математическая статистика?

Математическая статистика нужна для анализа данных и получения выводов о популяции на основе выборки. С ее помощью можно выявить закономерности, проверить гипотезы, прогнозировать и принимать решения.

Роль математической статистики в принятии решений

Математическая статистика играет важную роль в принятии решений во многих областях, где требуется анализ данных и выявление закономерностей. Она предоставляет набор инструментов и методов для обработки, интерпретации и использования статистических данных.

Одной из основных функций математической статистики является описание данных. С помощью статистических методов можно исследовать распределение данных, определить параметры распределений, выявить выбросы и аномалии. Это позволяет получить полное представление о данных и понять их характеристики и свойства.

Еще одной важной задачей математической статистики является проверка гипотез. С помощью статистических тестов можно проверить различные предположения и утверждения на основе имеющихся данных. Это помогает принимать обоснованные решения, основанные на статистических фактах и выводах.

Математическая статистика также используется для прогнозирования и построения моделей. С помощью статистических методов можно анализировать и прогнозировать будущие значения на основе имеющихся данных. Это позволяет принимать решения, учитывая возможные сценарии и их вероятности.

Кроме того, математическая статистика помогает в принятии решений на основе оценки рисков. С помощью статистических методов можно анализировать и оценивать риски различных событий и принимать решения, основанные на вероятностной оценке их возникновения и последствий.

Таким образом, математическая статистика играет важную роль в принятии решений, обеспечивая анализ и интерпретацию данных, проверку гипотез, прогнозирование и оценку рисков. Она позволяет принимать обоснованные и информированные решения, основанные на статистических фактах и выводах.

Видео по теме: