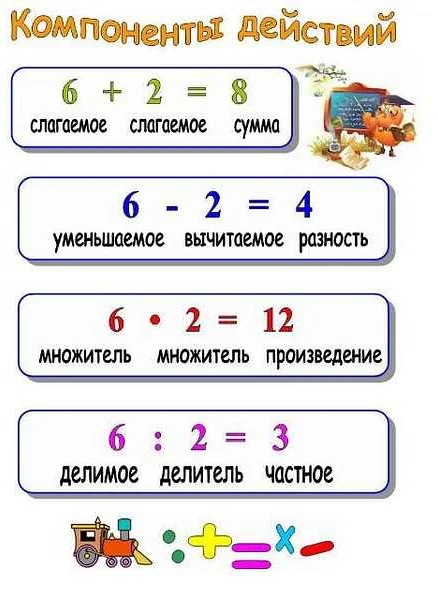
Что такое частные в математике

Частные в математике — это результат деления одного числа на другое. Частные могут быть целыми числами, десятичными дробями или дробями. Узнайте подробнее о понятии частных и их использовании в математике.

В математике понятие частного является одним из фундаментальных и используется в различных областях, начиная от арифметики и заканчивая дифференциальным исчислением. Частные позволяют решать задачи, связанные с делением, распределением и анализом данных. В этой статье мы рассмотрим основные понятия и примеры частных в математике.

Одним из базовых определений является частное чисел. Оно обозначает результат деления одного числа на другое. Например, частное чисел 10 и 2 равно 5, так как 10 разделить на 2 дает 5. В данном случае 10 называется делимым, а 2 — делителем. Частное числа может быть как целым числом, так и десятичной дробью или дробью.

В алгебре понятие частного расширяется и применяется к многочленам. Частное многочленов — это результат деления одного многочлена на другой. Например, если у нас есть многочлены 3x^2 + 4x + 2 и x + 1, то их частное будет равно 3x + 1. В данном случае 3x^2 + 4x + 2 — делимый, а x + 1 — делитель.

Частное является важным понятием не только в арифметике и алгебре, но и в других областях математики, таких как теория вероятностей, математическая статистика, математический анализ и теория чисел. Понимание основных понятий и примеров частных поможет в решении сложных математических задач и развитии аналитического мышления.

Определение частного в математике

Для нахождения частного двух чисел, первое число называется делимым, а второе число — делителем. Результатом деления является частное, которое обозначается символом «Q» или словом «частное».

Частное можно представить в виде десятичной дроби или обыкновенной дроби. В десятичной форме частное может быть бесконечной последовательностью цифр после запятой.

Например, если мы хотим разделить число 10 на 2, то 10 будет делимым, а 2 — делителем. Результатом деления будет число 5, так как 10 разделить на 2 равно 5.

В математике существуют также понятия остатка и целой части от деления, которые могут быть использованы вместе с частным.

Видео по теме:

Частное и деление

Деление — это арифметическая операция, позволяющая разделить одно число на другое и найти результат этого разделения, который и называется частным.

Чтобы найти частное двух чисел, нужно разделить делимое на делитель. Делимое — это число, которое мы делим, а делитель — это число, на которое мы делим.

Частное обозначается символом «/», который ставится между делимым и делителем. Например, если мы делим число 10 на число 2, то частное будет равно 10/2 = 5.

Важно учитывать, что в математике есть некоторые правила и ограничения в отношении деления. Например, на ноль делить нельзя, так как результатом такого деления будет бесконечность или неопределенность.

Также стоит помнить о понятии остатка от деления. Остатком называется число, которое остается после того, как делимое число разделено на делитель.

В общем случае, частное может быть как целым числом, так и дробным числом, в зависимости от того, какое число мы делим и на что делим.

Знание понятий частного и деления является основой для решения множества задач в математике и других науках, а также на практике в повседневной жизни.

Частное и десятичная дробь

Десятичная дробь — это способ представления дробного числа с использованием десятичной системы счисления. В десятичной дроби, числа разделены точкой, где целая часть числа находится слева от точки, а десятичная часть — справа.

При делении чисел, иногда результат может быть представлен в виде десятичной дроби. Например, при делении 1 на 3, результат будет 0.33333… В этом случае, десятичная дробь получается путем повторения одной или нескольких цифр после точки.

Десятичные дроби можно записывать и в виде конечных десятичных дробей, где количество цифр после точки ограничено. Например, 1/4 можно записать как 0.25, где 25 является конечной десятичной дробью.

Десятичные дроби могут быть представлены в различных форматах, таких как обыкновенная десятичная дробь или десятичная дробь с фиксированной точностью. В обыкновенной десятичной дроби, количество цифр после точки может быть разным для разных чисел. В десятичной дроби с фиксированной точностью, количество цифр после точки ограничено.

Десятичные дроби широко используются в нашей повседневной жизни, особенно при работе с деньгами и измерениями.

Понятие остатка от деления

Формально, остаток от деления числа a на число b можно представить следующим образом: a % b = r, где a – делимое, b – делитель, r – остаток от деления. Оператор % обозначает остаток от деления.

Например, при делении 10 на 3, остаток будет равен 1. Это можно записать следующим образом: 10 % 3 = 1.

Остаток от деления имеет множество применений в математике и программировании. Например, он используется для определения четности или нечетности числа, а также для проверки делимости числа на другое число.

В таблице ниже приведены примеры вычисления остатка от деления:

Делимое (a)Делитель (b)Остаток (a % b)

10	3	1
15	4	3
20	7	6

Частное и числительная дробь

Числительная дробь — это дробное число, в котором числитель и знаменатель представлены целыми числами. Числительная дробь может быть положительной или отрицательной.

Например, если мы имеем число 5 и число 2, то частное будет равно 2.5, что можно представить как десятичную дробь. Если мы хотим представить это в виде числительной дроби, то числитель будет равен 5, а знаменатель будет равен 2.

Частное и натуральные числа

Натуральные числа — это набор положительных целых чисел, начиная от 1 и бесконечно продолжающийся. Обозначаются символом N. Натуральные числа используются для подсчета объектов или описания их количества.

ДелительДелительЧастное

10	2	5
12	3	4
15	5	3

В таблице приведены примеры деления некоторых чисел. Делитель — это число, на которое происходит деление, делимое — это число, которое делится, а частное — это результат деления.

Частное и дробь

Частным двух чисел называется результат деления одного числа на другое. Если числа обозначаются как a и b, то частное можно записать как a/b или с помощью знака деления ÷.

Пример:

ДелимоеДелительЧастное

10	2	5
15	3	5
7	4	1.75

Дробь — это числовое выражение, состоящее из числителя и знаменателя, разделенных чертой. Числитель обозначает количество частей, а знаменатель — количество частей, на которые разделено целое число.

Примеры дробей:

• 1/2
• 3/4
• 5/6

В математике дроби используются для представления долей, долей чисел, нецелых чисел и результатов десятичных дробей.

Примеры вычисления частного в математике

ДелимоеДелительЧастное

10	2	5
15	3	5
20	4	5

В первом примере, когда делимое равно 10, а делитель равен 2, частное будет равно 5, так как 10 разделить на 2 равно 5.

Аналогично, во втором и третьем примере частное также будет равно 5. Это демонстрирует тот факт, что при делении чисел, когда делимое кратно делителю, частное всегда будет одинаковым.

Вычисление частного является важной математической операцией и широко используется в различных областях, таких как алгебра, геометрия, физика и экономика.

Вопрос-ответ:

Что такое частные в математике?

Частные в математике — это результат деления одного числа на другое.

Как найти частное двух чисел?

Чтобы найти частное двух чисел, нужно разделить одно число на другое. Например, частное чисел 10 и 2 равно 5, так как 10 разделить на 2 равно 5.

Какие основные свойства имеют частные в математике?

Частные в математике обладают следующими основными свойствами: коммутативность (порядок чисел не влияет на результат деления), ассоциативность (результат деления не зависит от порядка выполнения операций), дистрибутивность (деление можно распределить по сложению или умножению), нейтральный элемент (деление на 1 не меняет число) и отсутствие деления на 0 (деление на 0 является недопустимой операцией).

Можете привести примеры использования частных в математике?

Конечно! Частные используются во многих областях математики и повседневной жизни. Например, при расчете среднего значения, при нахождении процентов, при делении предметов на группы и т.д. В математических формулах и уравнениях также часто встречаются частные.