Чем система отличается от совокупности в математике

Система и совокупность в математике — два разных понятия. Система представляет собой упорядоченное множество элементов, где каждый элемент связан с другими элементами определенными отношениями. Совокупность же представляет собой неупорядоченное множество элементов, где каждый элемент может быть независим от других элементов. Разница между системой и совокупностью заключается в их структуре и связях между элементами.

В математике понятие «система» имеет свои особенности и отличается от понятия «совокупность». Система — это упорядоченное множество элементов или объектов, которые взаимодействуют между собой и образуют единую целостность. В отличие от системы, совокупность представляет собой неупорядоченное множество элементов, связь между которыми может быть произвольной.

В системе каждый элемент имеет свою роль и функцию, которая согласована с целями и общими правилами системы. Элементы системы взаимодействуют между собой и влияют друг на друга, образуя определенные взаимосвязи и зависимости. В совокупности же каждый элемент может быть независимым и не связанным с другими элементами.

Еще одним отличием системы от совокупности является наличие в системе структуры и организации. Система имеет определенные правила и принципы, по которым функционирует, а также определенную иерархию элементов. Совокупность же не имеет строгой структуры и организации.

Интересно, что система может состоять из нескольких совокупностей, но это не делает ее совокупностью. Совокупность — это просто множество элементов, а система — это упорядоченное и организованное множество, где каждый элемент имеет свою роль и функцию.

Определение и характеристики системы в математике

Основные характеристики системы в математике:

1. Элементы:

Система состоит из отдельных элементов, которые могут быть числами, объектами, функциями и т. д. Элементы могут быть как конечными, так и бесконечными.

2. Взаимодействие:

Элементы системы взаимодействуют друг с другом. Взаимодействие может быть определено различными математическими отношениями, операциями или функциями.

3. Целостность:

Система обладает свойством целостности, то есть элементы и их взаимодействие образуют определенную структуру или организацию, которая отличает систему от простой совокупности элементов.

4. Взаимозависимость:

Элементы системы взаимозависимы друг от друга. Изменение одного элемента может вызывать изменение других элементов системы.

5. Свойства:

Система может иметь определенные свойства или характеристики, которые могут быть изучены и описаны с помощью математических методов и моделей.

В математике системы широко используются для анализа сложных структур и процессов, а также для моделирования реальных явлений.

Понятие системы в математике

В математике понятие системы используется для описания совокупности связанных элементов или объектов, которые образуют единое целое и взаимодействуют между собой.

Система в математике может быть определена как упорядоченное множество элементов, для которых заданы определенные правила взаимодействия или зависимости. Каждый элемент системы называется компонентом. Важно отметить, что сами компоненты системы могут быть объектами, числами, уравнениями или другими математическими сущностями.

Основная особенность системы в математике заключается в том, что изменение одного компонента может влиять на другие компоненты и на всю систему в целом. Таким образом, система является динамической и может иметь различные состояния в зависимости от состояний ее компонентов.

Одним из примеров системы в математике может быть система уравнений, где каждое уравнение является компонентом системы, а решение системы представляет собой набор значений переменных, удовлетворяющих всем уравнениям системы.

Понятие системы в математике имеет широкое применение и используется для моделирования и анализа различных явлений и процессов. Математические модели систем могут помочь в исследовании сложных взаимосвязей и прогнозировании поведения системы в различных условиях.

Таким образом, система в математике отличается от совокупности тем, что она представляет собой не просто набор элементов, а объединенное целое, где каждый элемент взаимодействует с другими элементами и влияет на состояние всей системы.

Характеристики системы в математике

1. Элементы системы: система состоит из отдельных элементов, которые могут быть числами, символами, функциями или другими математическими объектами.
2. Отношения: элементы системы могут быть связаны между собой определенными отношениями, которые определяют правила взаимодействия между ними.
3. Структура: система имеет определенную структуру, которая определяет порядок и организацию элементов системы.
4. Ограничения: система может иметь определенные ограничения или условия, которым должны удовлетворять элементы системы или их отношения.
5. Цели и функции: система может иметь определенные цели или функции, которые определяют ее назначение и предназначение.
6. Иерархия: элементы системы могут быть организованы в иерархическую структуру, где некоторые элементы являются подчиненными другим элементам.

Характеристики системы в математике помогают в изучении и анализе сложных математических структур и явлений, а также в разработке методов и моделей для их описания и предсказания.

Определение и характеристики совокупности в математике

Совокупность в математике представляет собой собрание или группу элементов, которые могут быть какими угодно объектами или явлениями. Элементы совокупности называются членами или элементами совокупности.

Совокупность может быть конечной или бесконечной. Конечная совокупность содержит конечное число элементов, тогда как бесконечная совокупность содержит несчётное число элементов.

Совокупность может быть задана явно или неявно. Явное задание совокупности предполагает перечисление всех ее элементов, например: {1, 2, 3, 4, 5}. Неявное задание совокупности предполагает определение правил, по которым можно определить, является ли элемент членом совокупности, например: {x | x > 0}.

Важным понятием, связанным со совокупностью, является понятие подмножества. Подмножество — это совокупность, состоящая из элементов исходной совокупности, принадлежащих определенным условиям. Например, если исходная совокупность — это {1, 2, 3, 4, 5}, то подмножество может быть {1, 3, 5}, состоящее только из нечетных чисел.

Совокупность в математике представляет собой важный инструмент для описания и анализа различных явлений, объектов и процессов. Она позволяет систематизировать информацию и делать выводы на основе обобщенных данных.

Характеристики совокупностиОписание

Мощность совокупности	Количество элементов в совокупности.
Пустая совокупность	Совокупность, не содержащая ни одного элемента.
Равные совокупности	Две совокупности, имеющие одинаковое количество элементов.
Совокупность как множество	Совокупность может быть представлена в виде множества, где каждый элемент совокупности является элементом множества.
Операции над совокупностями	В математике существуют операции над совокупностями, такие как объединение, пересечение, разность и декартово произведение.

Понятие совокупности в математике

В математике понятие совокупности применяется для описания группы элементов, объединенных определенным свойством или условием. Совокупность представляет собой набор объектов, которые могут быть числами, предметами, событиями или любыми другими элементами, зависящими от контекста задачи.

Совокупность в математике обычно обозначается фигурными скобками и содержит элементы, разделенные запятыми. Например, совокупность всех целых чисел от 1 до 10 можно записать следующим образом:

{

1, 2, 3, 4, 5, 6, 7, 8, 9, 10

}

Совокупность может быть конечной или бесконечной. Кроме того, она может быть упорядоченной или неупорядоченной. В случае упорядоченной совокупности элементы располагаются в определенном порядке, в то время как в неупорядоченной порядок элементов не имеет значения.

Совокупность может также быть пустой, то есть не содержать ни одного элемента. Она обычно обозначается пустыми фигурными скобками {} или символом ∅. Например, пустая совокупность всех натуральных чисел меньше 1 записывается следующим образом:

{}

или

∅

Совокупность может быть использована для определения множества, которое является более формализованным понятием в математике. Множество состоит из совокупности элементов, удовлетворяющих определенному свойству или условию.

Важно отметить, что совокупность и система — это разные понятия в математике. Система обычно описывает связанные между собой элементы или правила, которые характеризуют определенный порядок или взаимодействие. Совокупность, напротив, фокусируется на группе элементов, без учета их взаимосвязи или порядка.

Характеристики совокупности в математике

Совокупность в математике представляет собой набор элементов, которые объединены общим свойством или признаком. Основные характеристики совокупности включают:

• Элементы: совокупность состоит из отдельных элементов, которые могут быть числами, объектами, событиями или другими математическими объектами.
• Объем: количество элементов в совокупности определяет ее объем. Объем совокупности может быть конечным или бесконечным.
• Свойства: каждый элемент совокупности обладает определенными свойствами или признаками, которые объединяют их в совокупность.
• Распределение: элементы совокупности могут быть распределены по различным категориям или группам на основе их свойств или признаков.
• Упорядоченность: элементы совокупности могут быть упорядочены по определенному критерию, например, по возрастанию или убыванию.

Характеристики совокупности помогают нам анализировать и описывать ее состав, структуру и свойства. Они являются важным инструментом в математическом анализе и статистике, а также в других областях, где требуется работа с наборами элементов.

Отличия между системой и совокупностью

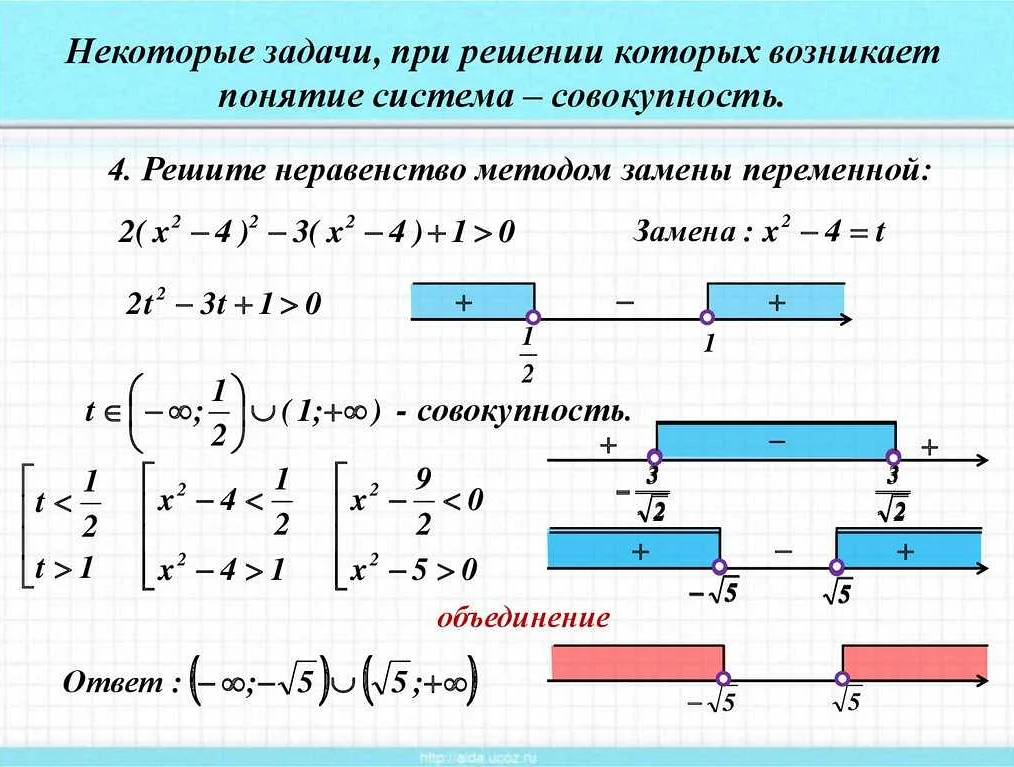
Совокупность — это набор элементов, которые могут быть связаны друг с другом только на основе какого-либо общего признака. В совокупности элементы не обязательно взаимосвязаны друг с другом и могут находиться в любом порядке. Элементы могут быть собраны вместе без какой-либо определенной структуры. Например, совокупность всех целых чисел или совокупность всех студентов в университете.

Система — это упорядоченная совокупность элементов, которая имеет определенную структуру и взаимосвязь между элементами. Элементы системы взаимодействуют между собой и образуют целостное целое. В системе каждый элемент играет свою роль и выполняет свои функции в соответствии с заданной структурой. Например, система линейных уравнений или система органов человека.

Основные отличия между системой и совокупностью:

1. Структура: система имеет определенную структуру, в то время как совокупность не имеет определенной структуры.
2. Взаимосвязь: элементы системы взаимосвязаны и взаимодействуют друг с другом, в то время как элементы совокупности могут быть независимыми и не взаимосвязанными.
3. Роль и функции: каждый элемент системы играет свою роль и выполняет свои функции в соответствии с заданной структурой, в то время как элементы совокупности могут быть однородными и выполнять одну и ту же функцию.
4. Целостность: система образует целостное целое, в то время как совокупность не обязательно образует целостность.

Использование понятий системы и совокупности зависит от контекста и конкретной задачи. Понимание и различение этих понятий позволяет математикам анализировать и описывать различные объекты и явления в мире.

Различия в определении

Система — это упорядоченное множество элементов, где каждый элемент имеет свою роль и взаимосвязь с другими элементами. В системе каждый элемент представляет собой часть целого, и изменение одного элемента может повлиять на остальные. Элементы системы могут быть связаны логически, функционально или просто находиться в определенной взаимосвязи друг с другом.

Совокупность, с другой стороны, это неупорядоченное множество элементов, которые могут быть связаны между собой только путем принадлежности к этой совокупности. Элементы совокупности могут быть произвольными и не обязательно иметь какую-либо взаимосвязь.

Важно отметить, что система может быть рассмотрена как совокупность элементов, но не каждая совокупность является системой. В системе элементы связаны между собой и выполняют определенную функцию или цель, в то время как в совокупности элементы могут быть случайными и не иметь какой-либо организации или цели.

Например, можно представить систему в виде таблицы, где каждый столбец представляет собой элемент системы, а каждая строка — различные свойства или характеристики этих элементов. Такая таблица позволяет упорядочить элементы и показать их взаимосвязь. Совокупность, с другой стороны, может быть представлена простым списком элементов без какой-либо организации или связи между ними.

Элементы системыСвойства/характеристики

Элемент 1	Свойства 1
Элемент 2	Свойства 2
Элемент 3	Свойства 3

Таким образом, система и совокупность имеют различные определения и свойства. Система — это упорядоченное множество элементов с взаимосвязью и целью, в то время как совокупность — это неупорядоченное множество элементов без какой-либо организации или цели.

Различия в характеристиках

Система — это упорядоченное множество объектов, которые связаны между собой определенными правилами или законами. В системе каждый объект имеет свое определенное место и роль, и его действия или свойства зависят от других объектов в этой системе.

Совокупность — это неупорядоченное множество объектов, которые могут быть связаны между собой или не связаны вообще. В отличие от системы, каждый объект в совокупности имеет свою индивидуальность и независимость, и его действия или свойства могут не зависеть от других объектов.

Таким образом, система характеризуется упорядоченностью, взаимосвязью и взаимозависимостью объектов, а совокупность — неупорядоченностью и независимостью объектов.

Пример: В системе могут быть представлены уравнения, в которых каждое уравнение зависит от других уравнений в системе. В совокупности могут быть представлены наборы чисел, которые не имеют какой-либо взаимосвязи или зависимости друг от друга.

Видео по теме:

Чем система отличается от совокупности в математике?

Система и совокупность — это два разных понятия в математике. Система представляет собой упорядоченное множество элементов, где каждый элемент связан с другими элементами определенными правилами. Совокупность же представляет собой неупорядоченное множество элементов, где элементы могут быть связаны между собой или не связаны вообще.

Какие основные характеристики у системы в математике?

Основные характеристики системы в математике включают ее упорядоченность, взаимосвязь элементов внутри системы, наличие определенных правил и законов, которым подчиняется система, а также возможность изменения системы при добавлении или удалении элементов.

В чем суть понятия системы в математике?

Понятие системы в математике описывает упорядоченное множество элементов, где каждый элемент связан с другими элементами по определенным правилам. В системе каждый элемент играет определенную роль и взаимодействует с другими элементами для достижения определенной цели или результата.

Какие примеры систем можно привести в математике?

В математике есть множество примеров систем, таких как системы уравнений, системы координат, системы логических утверждений, системы аксиом и т. д. В каждом из этих примеров элементы системы взаимодействуют друг с другом и подчиняются определенным правилам и законам.

Какова роль систем в математике?

Системы играют важную роль в математике, так как они позволяют упорядочить и организовать множество элементов. С помощью систем можно решать сложные задачи, находить закономерности, моделировать различные процессы и явления. Они также позволяют развивать логическое мышление и аналитические навыки.

Чем система отличается от совокупности в математике?

Система и совокупность — это два разных понятия в математике. Система — это совокупность элементов, в которой каждый элемент взаимодействует с другими элементами внутри этой системы, образуя взаимосвязи и зависимости. Совокупность же представляет собой просто набор отдельных элементов, не имеющих между собой никаких взаимосвязей или зависимостей.