Генеральная совокупность в математике: определение и примеры использования

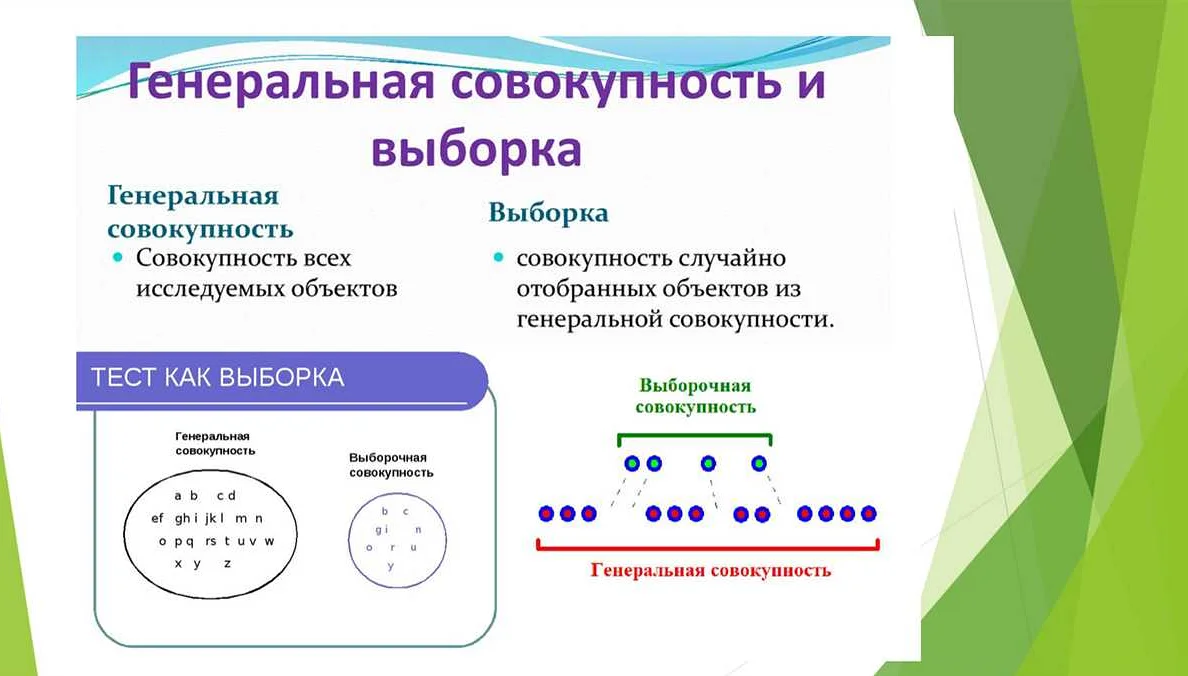
Генеральная совокупность — это множество всех элементов, которые могут быть рассмотрены в исследовании, включая все возможные значения. В математике она играет важную роль в статистическом анализе и позволяет проводить репрезентативные и точные выводы на основе данных о выборочной совокупности. Понимание этого термина может быть полезно для всех, кто работает в области статистики и анализа данных.

Генеральная совокупность — это один из основных терминов математической статистики, который имеет важное значение для проведения исследований и анализа данных. Это множество всех возможных значений, которые могут быть получены при изучении конкретного явления или процесса.

Для того чтобы получить информацию о генеральной совокупности, проводятся исследования ее части — выборки. Выборка — это подмножество генеральной совокупности, которое используется для анализа. Изучение выборки позволяет дать оценку параметров генеральной совокупности и сделать выводы о ее свойствах.

Одним из примеров использования генеральной совокупности является определение среднего значения и стандартного отклонения. При этом изучается выборка, из которой находят среднее значение значений и стандартное отклонение от этого значения. Эта информация позволяет сделать выводы о свойствах генеральной совокупности.

В математике генеральная совокупность является одним из основных понятий, которое используется в статистике, теории вероятностей, экономике, социологии и других областях науки. Понимание этого термина имеет важное значение для создания статистических моделей и прогнозирования различных явлений и процессов.

Что такое генеральная совокупность?

Генеральная совокупность в математике — это совокупность всех возможных значений определенной величины. Генеральная совокупность может быть бесконечной или конечной, и часто используется для описания свойств определенного процесса, объекта или населения.

Определение генеральной совокупности широко используется в статистике, где она является основой статистических исследований. Например, если мы хотим изучить образование в нашей стране, генеральной совокупностью будет все население России в возрасте от 18 лет.

Важно отметить, что изучение генеральной совокупности может быть чрезвычайно сложным и занимать много времени и ресурсов. Поэтому исследователи часто используют выборку — подмножество генеральной совокупности, чтобы получить более точные данные.

Наконец, при изучении генеральной совокупности важно учитывать, что она может меняться со временем и подвергаться внешним влияниям, которые могут повлиять на результаты исследований.

Зачем нужна генеральная совокупность в математике?

Генеральная совокупность является одним из основных понятий статистики и математики в целом. Она описывает все возможные результаты эксперимента или наблюдения на интересующий нас вопрос.

Зачем же нам нужна генеральная совокупность? Во-первых, она позволяет проводить статистические исследования с высокой точностью. Если мы изучаем группу людей, например, то результаты нашего исследования будут надежными, если мы будем знать генеральную совокупность, то есть всех людей в данном обществе или стране.

Во-вторых, генеральная совокупность помогает сравнивать результаты различных исследований и наблюдений. Благодаря общей картине исследования мы можем лучше понимать, как наше исследование соотносится с другими, проводимыми в этой же области.

Наконец, генеральная совокупность позволяет нам строить верные выводы и делать правильные решения на основе статистических данных. Если мы хотим принимать обоснованные решения в какой-то ситуации, то необходимо учитывать все возможные факторы и знать генеральную совокупность.

Таким образом, генеральная совокупность является основой для проведения любых статистических исследований и позволяет получить достоверные результаты и делать обоснованные выводы на основе данных.

Как определить генеральную совокупность?

Генеральная совокупность — это множество всех объектов, явлений или событий, к которым применимо изучаемое свойство. Определить генеральную совокупность можно на основе цели исследования:

• Если цель исследования — изучение всех объектов с определенным свойством, то генеральную совокупность можно определить как все объекты, подходящие под описание этого свойства. Например, если мы исследуем рост всех девушек в возрасте от 18 до 25 лет, то генеральной совокупностью будут все девушки этого возраста.
• Если цель исследования — выяснить свойства группы объектов, то генеральную совокупность можно определить как множество всех объектов, из которых случайным образом была выбрана данная группа. Например, если мы исследуем студентов определенного факультета, то генеральной совокупностью будут все студенты этого факультета.

Для более точного определения генеральной совокупности могут использоваться статистические методы, такие как выборочное исследование или анализ данных. Следует учитывать, что определение генеральной совокупности имеет огромное значение для проведения качественного и точного исследования.

Как собрать данные для генеральной совокупности?

Сбор данных для генеральной совокупности является важным этапом и требует тщательной подготовки и планирования.

Первоначально необходимо определить генеральную совокупность – это все объекты/люди/ситуации, которые подходят под категорию исследования и включаются в выборку. Определение генеральной совокупности позволяет определить, какие группы людей/ситуаций будут включены в исследование.

Далее нужно разработать план сбора данных. Это может включать выбор метода сбора данных (например, опросы, интервью, наблюдение) и определение размера выборки. Размер выборки должен быть достаточно большим, чтобы дать точную оценку генеральной совокупности, но не слишком большим, чтобы сбор данных был невыполнимым.

После этого можно начать сбор данных. Здесь важно следовать разработанному плану сбора данных, чтобы исключить возможность искажения результатов исследования. Также важно уделять внимание контролю качества данных, чтобы избежать ошибок при их обработке и анализе.

Важным этапом является анализ данных. Здесь проводится обработка исходной информации и её представление в удобном виде для последующей интерпретации. Значительную роль при этом играет выбор инструментов статистического анализа и определение критериев, по которым будут оцениваться полученные данные.

В целом, сбор данных для генеральной совокупности требует систематичности, внимательности и планирования. Это позволяет получить более точные результаты исследования и сделать выводы, которые можно применять на практике.

Как обработать данные генеральной совокупности?

Одним из методов обработки данных генеральной совокупности является вычисление её основных характеристик, таких как среднее значение, медиана, мода, стандартное отклонение, интерквартильный размах и др.

Для вычисления среднего значения необходимо найти сумму всех значений в генеральной совокупности и разделить на общее число значений. Для вычисления медианы нужно упорядочить все значения в порядке возрастания или убывания и найти середину ряда. Если число значений нечетное, то медиана – это среднее значение двух центральных значений. Если число значений четное, то медиана – это среднее значение двух соседних значений по середине ряда.

Другим методом обработки данных генеральной совокупности является анализ распределения характеристик в выборке, которая является частью генеральной совокупности. Для этого используются графические методы, такие как диаграммы рассеивания, гистограммы, ящики с усами и диаграммы квантилей. Они позволяют оценить форму распределения, наличие выбросов и возможную корреляцию между характеристиками.

Еще одним методом обработки данных генеральной совокупности является использование статистических тестов, которые позволяют проверить гипотезы о связи между характеристиками или о различии характеристик в разных выборках. Например, t-тест Стьюдента используется для проверки равенства средних значений двух независимых выборок, а корреляционный анализ – для оценки связи между двумя переменными.

1. Вычисление основных характеристик
2. Анализ распределения характеристик в выборке
3. Использование статистических тестов

Как использовать генеральную совокупность в статистических расчетах?

Генеральная совокупность в статистических расчетах очень важна, так как именно она позволяет оценить параметры самой выборки. Но как использовать генеральную совокупность в расчетах?

1. Определите генеральную совокупность

Перед тем, как начать расчеты, необходимо определить генеральную совокупность. Например, если вам нужно проанализировать доходы жителей города, то генеральной совокупностью будут являться все жители этого города.

2. Определите выборку

Выборка — это часть генеральной совокупности, которая будет использоваться для проведения статистических расчетов. Она должна быть достаточно большой, чтобы ее результаты можно было обобщить на всю генеральную совокупность. Например, если вы решите проанализировать доходы жителей города, то выборкой могут стать все жители одного или нескольких районов города.

3. Проведите статистические расчеты

После того, как вы определили генеральную совокупность и выборку, вы можете начать проводить статистические расчеты. Например, вы можете рассчитать средний доход жителей выбранной выборки и сравнить его с средним доходом всей генеральной совокупности. Также можно проводить более сложные статистические анализы, такие как корреляционный анализ, регрессионный анализ и т.д.

4. Оцените точность результатов

Оценка точности результатов является важной частью статистических расчетов. Чтобы оценить точность результатов, необходимо провести дополнительные анализы, такие как определение стандартного отклонения или ошибок выборки. Это поможет определить, насколько точны полученные результаты и насколько их можно обобщить на всю генеральную совокупность.

В заключение, использование генеральной совокупности в статистических расчетах позволяет проводить более точные анализы и получать более достоверные результаты. При правильном использовании генеральной совокупности, вы сможете получить репрезентативную информацию о целевой группе, что поможет принимать взвешенные решения.

Пример использования генеральной совокупности в математике: расчет среднего арифметического

Генеральная совокупность – это совокупность всех элементов, которые могут быть подвергнуты исследованию, исследовательскими методами. В математике, генеральной совокупностью могут быть числа, значения, некоторые характеристики, и так далее.

Одним из способов использования генеральной совокупности является расчет среднего арифметического. Для этого необходимо получить данные о каждом элементе генеральной совокупности и подсчитать их общую сумму. Затем, эту сумму следует разделить на количество элементов генеральной совокупности. Результатом будет среднее арифметическое.

Например, предположим, что мы исследуем генеральную совокупность, состоящую из 7 чисел: 1, 3, 5, 7, 9, 11, 13. Сначала, необходимо подсчитать их общую сумму: 1+3+5+7+9+11+13=49. Затем, мы делим эту сумму на количество элементов генеральной совокупности (7): 49/7=7. Таким образом, среднее арифметическое равно 7.

Такой расчет среднего арифметического может быть полезным, например, при анализе данных в бизнесе, финансах, экономике, социологии и других областях. Он позволяет оценить типичное значение в генеральной совокупности и использовать его в дальнейшем анализе и принятии решений.

Пример использования генеральной совокупности в экономике: анализ рынка

Для проведения анализа рынка, требуется изучение генеральной совокупности, которая представляет собой полный набор элементов, относящихся к данной сфере. Например, если мы анализируем рынок автомобилей, то генеральной совокупностью являются все автомобили, продаваемые в данной стране или регионе.

Одной из задач анализа является оценка размеров и структуры генеральной совокупности. Для этого используются различные методы, такие как опросы, определение объемов продаж, изучение конкуренции и т.д. Важно получить максимально точную информацию о генеральной совокупности, чтобы правильно оценить текущее состояние рынка и выработать стратегию развития.

Другим важным аспектом анализа генеральной совокупности является выборка. Для того, чтобы провести статистический анализ рынка, необходимо выбрать определенное количество элементов из генеральной совокупности и проанализировать их. Это делается с помощью различных методов, например, случайной выборки.

В результате анализа генеральной совокупности можно получить ценные данные о состоянии рынка, такие как потенциальный объем продаж, уровень конкуренции, потребительский спрос и т.д. Таким образом, использование генеральной совокупности в экономике является необходимым инструментом для успешного анализа рынка и разработки стратегии бизнеса.

Пример использования генеральной совокупности в биологии: исследование популяции

Генеральная совокупность в биологии может определяться как общее количество организмов, составляющих конкретную популяцию в определенном месте и времени. Изучение генеральной совокупности с целью выявления закономерностей в поведении популяции или влияния на нее внешних факторов может быть полезным инструментом при проведении биологических исследований.

Рассмотрим пример: если мы хотим изучить поведение популяции лис в лесу, генеральной совокупностью, в данном случае, будут все лисы, находящиеся в данном лесу. На основе этой генеральной совокупности мы можем проанализировать поведение лис, например, их движение, питание, размножение и взаимодействие с другими организмами в лесу. Результаты исследования генеральной совокупности могут помочь нам понять, как изменения в среде обитания влияют на поведение лис и других животных, находящихся в этом лесу.

Важно отметить, что для изучения генеральной совокупности, требуется собирать информацию о каждом организме в рамках выбранного исследования. Это может быть трудоемкой задачей, особенно для больших популяций. Однако, результаты такого исследования могут быть более точными и иметь больший научный вес, чем результаты изучения только определенной части популяции.

Какие ограничения есть у генеральной совокупности в математике?

Генеральная совокупность — это совокупность всех объектов, описываемых заданным признаком или характеристикой, в математике. Однако, существуют определенные ограничения, которые могут повлиять на описание и использование генеральной совокупности.

• Ограничения доступности информации: В некоторых случаях, может быть невозможно получить доступ ко всем объектам генеральной совокупности, из-за ограничений на сбор и использование данных.
• Ограничения точности описания: Как правило, описание генеральной совокупности основывается на ее выборке и ограничено объемом данных, что может привести к некоторым неточностям и упрощениям в описании совокупности.
• Ограничения изменяемости генеральной совокупности: В некоторых случаях, генеральная совокупность может быть незначительно изменена во времени или по мере появления новых данных, что может повлиять на то, как она была описана или использована в математических моделях.

Кроме того, в математике может быть использовано ограниченное число методов и техник для анализа и описания генеральной совокупности, в зависимости от ее природы и объема данных. Несмотря на это, генеральная совокупность все еще является важным концептом для многих областей математики, в том числе для статистики, теории вероятности и логики.

Как использовать генеральную совокупность для принятия решений?

Генеральная совокупность — это множество всех возможных значений для определенного параметра в исследуемой ситуации. Она является основой для принятия точных и обоснованных решений.

Для использования генеральной совокупности для принятия решений необходимо провести статистический анализ выборочных данных. На основе этого анализа можно сделать выводы о генеральной совокупности и принимать решения на основе полученной информации.

Например, если необходимо принять решение о продаже продукта в определенном регионе, можно провести исследование выборки потенциальных клиентов и на основе полученных данных сделать выводы о потенциальной прибыльности и рисках продажи продукта. Это позволит принять обоснованное решение.

Важно также учитывать возможные ограничения и неопределенности при работе с генеральной совокупностью. Например, если исследование проводится на основе данных прошлых лет, необходимо учитывать возможные изменения в экономической и социальной сфере, которые могут повлиять на результаты исследования.

Итак, использование генеральной совокупности для принятия решений позволяет получать точные и обоснованные выводы, основанные на изучении большого количества данных. Однако при работе с генеральной совокупностью важно учитывать неопределенности и возможные ограничения, чтобы принимать решения, основанные на реалистичных оценках.

Вопрос-ответ:

Как определить генеральную совокупность в математике?

Генеральная совокупность в математике — это общая совокупность всех элементов, которые изучаются в определенной выборке. Она может быть любого размера, и ее определение зависит от контекста исследования.

Какую роль играет генеральная совокупность в статистике?

Генеральная совокупность играет ключевую роль в статистике, так как она позволяет сделать выводы о характеристиках выборки и сделать общие выводы о всех элементах совокупности.

Можно ли установить характеристики генеральной совокупности?

Да, можно установить характеристики генеральной совокупности, используя методы математической статистики. Например, можно вычислить среднее значение и стандартное отклонение генеральной совокупности на основе выборки.

Как выбрать правильный размер выборки для получения точных результатов?

Размер выборки должен быть достаточно большим для получения достоверных результатов. Обычно рекомендуется, чтобы размер выборки составлял не менее 30 элементов. Однако, для точных результатов лучше использовать большие выборки.

Какие методы можно использовать для выборки генеральной совокупности?

Существует несколько методов для выборки генеральной совокупности, включая простую случайную выборку, стратифицированную выборку, кластерную выборку и выборку по критериальным признакам.

Какие примеры можно привести использования генеральной совокупности в науке и бизнесе?

Генеральная совокупность может быть использована в научных исследованиях для получения точных результатов и выводов, а также в бизнесе для оценки рынка, улучшения продуктов и услуг.

Что такое стандартная ошибка среднего и как ее вычислить?

Стандартная ошибка среднего — это мера дисперсии выборочного среднего относительно истинного среднего значения генеральной совокупности. Ее можно вычислить, используя формулу: s/корень n, где s — стандартное отклонение выборки, а n — размер выборки.

Видео по теме: