Совокупность в математике как обозначается

Совокупность в математике обозначается символом {}. Она представляет собой набор элементов, объединенных общими свойствами или условиями. Примеры использования совокупности в математике и ее обозначение.

Совокупность — это одно из фундаментальных понятий математики, которое используется для описания и анализа группы элементов, объединенных по некоторому признаку или свойству. Совокупности широко применяются в различных областях математики, а также в других науках, где требуется упорядочить или классифицировать объекты.

В математике совокупность обычно обозначается специальным символом, который указывает на множество элементов, входящих в данную совокупность. Например, для обозначения совокупности натуральных чисел используется символ N, для совокупности целых чисел — символ Z, для совокупности действительных чисел — символ R и т.д.

Совокупности играют ключевую роль в математическом анализе, теории множеств, теории вероятности, алгебре и других разделах математики. Они позволяют строить различные модели, описывающие множества, отношения и операции над ними. Благодаря совокупностям математики удается формализовать и абстрагировать сложные явления, что позволяет получать новые знания и решать различные практические задачи.

Использование совокупностей в математике имеет широкий спектр применений. Например, они могут быть использованы для определения области значений функций, описания наборов данных, моделирования статистических явлений, создания алгоритмов и многое другое. Благодаря точным математическим обозначениям совокупностей, их свойствам и операциям над ними, математики и другие ученые могут проводить систематические исследования и делать точные выводы.

Совокупность в математике: определение и области применения

Одна из основных областей, где используется понятие совокупности, — это теория множеств. В теории множеств совокупность представляется в виде множества, состоящего из элементов. Множество может быть конечным или бесконечным, и его элементы могут быть числами, объектами или другими множествами.

Совокупности также широко применяются в статистике и вероятности. Например, в статистике совокупность может представлять собой группу людей, популяцию или набор данных. Применение совокупностей в статистике позволяет анализировать и делать выводы о всей группе, основываясь на данных, полученных только из выборки.

Вероятностная теория также использует понятие совокупности для описания возможных исходов или событий. Совокупность всех возможных исходов называется пространством элементарных исходов, а отдельные элементы этой совокупности — элементарными событиями.

Кроме того, совокупности применяются в других областях математики, таких как логика, алгебра, геометрия и теория чисел. В каждой из этих областей совокупности используются для описания и классификации объектов, исследования их свойств и построения логических заключений.

Таким образом, понятие совокупности играет важную роль в математике и находит широкое применение в различных ее областях. Оно позволяет систематизировать и анализировать элементы, объединенные общими свойствами или правилами, и строить логические выводы на основе этих данных.

Видео по теме:

Множество элементов и их связь в совокупности

Связь между элементами множества может быть представлена различными способами, в зависимости от конкретной задачи или условий. Однако наиболее распространенными способами представления связи между элементами множества являются:

Способ представленияОписание

Диаграмма Эйлера	Графическое представление множеств и их взаимоотношений с помощью пересекающихся окружностей или других фигур.
Матрица связей	Таблица, в которой указывается, какие элементы множества связаны между собой, а какие нет.
Граф	Совокупность вершин и ребер, где вершины представляют элементы множества, а ребра — связи между элементами.

Выбор конкретного способа представления связи между элементами множества зависит от задачи и требований к наглядности и удобству представления информации.

Примеры использования совокупности в математике

1. Статистика: совокупность может использоваться для описания набора данных. Например, можно представить совокупность результатов экзамена или опроса.
2. Теория множеств: совокупность может быть использована для определения множества элементов с общими свойствами. Например, можно представить совокупность всех четных чисел или всех красных фруктов.
3. Теория вероятности: совокупность может использоваться для описания пространства элементарных событий. Например, можно представить совокупность возможных исходов при подбрасывании монеты.
4. Алгебра: совокупность может использоваться для определения группы элементов с определенными свойствами. Например, можно представить совокупность всех целых чисел или всех положительных вещественных чисел.

Это лишь несколько примеров использования совокупности в математике. Совокупность является важным инструментом для описания и анализа данных в различных математических дисциплинах.

Вопрос-ответ:

Что такое обозначение совокупности в математике?

Обозначение совокупности в математике представляет собой способ записи или описания группы элементов, объединенных определенным правилом или свойством.

Какие символы обычно используются для обозначения совокупности в математике?

Для обозначения совокупности в математике часто используются символы, такие как фигурные скобки { }, вертикальная черта | или двоеточие : . Например, {x | x > 0} обозначает множество всех x, таких что x больше нуля.

Какие примеры применения обозначения совокупности в математике?

Обозначение совокупности широко используется в различных областях математики. Например, в теории множеств с помощью обозначения совокупности можно записать множество всех натуральных чисел {1, 2, 3, …}, множество всех четных чисел {2, 4, 6, …} и так далее. Также обозначение совокупности используется в математической логике для записи условий и ограничений, например, {x | x > 5} означает множество всех x, которые больше пяти.

Как использовать обозначение совокупности для записи условий и ограничений?

Для использования обозначения совокупности для записи условий и ограничений нужно указать переменную, которая будет принимать значения из совокупности, а затем описать условие или ограничение, которому должны удовлетворять эти значения. Например, если нужно записать множество всех четных чисел, можно использовать обозначение {x | x % 2 = 0}, где x — переменная, а x % 2 = 0 — условие, что x делится на 2 без остатка.

Различные типы совокупностей и их характеристики

В математике существует несколько различных типов совокупностей, каждый из которых имеет свои характеристики и особенности.

• Пустая совокупность — это совокупность, не содержащая ни одного элемента. Она обозначается символом ∅. Например, если у нас нет ни одной цифры, мы можем представить это как пустую совокупность.
• Единичная совокупность — это совокупность, содержащая только один элемент. Она обозначается фигурной скобкой { } с элементом внутри. Например, совокупность всех натуральных чисел от 1 до 1 будет выглядеть как {1}.
• Конечная совокупность — это совокупность, содержащая конечное количество элементов. Она обозначается фигурными скобками с элементами внутри, разделенными запятыми. Например, совокупность состоящая из трех первых целых чисел будет выглядеть как {1, 2, 3}.
• Бесконечная совокупность — это совокупность, содержащая несчетное количество элементов. Она обозначается фигурными скобками с элементами внутри, разделенными запятыми, и многоточием для обозначения бесконечности. Например, совокупность всех натуральных чисел будет выглядеть как {1, 2, 3, …}.

Каждый тип совокупности имеет свои уникальные свойства и может использоваться в различных математических контекстах в зависимости от поставленной задачи.

Операции над совокупностями и их свойства

Объединение: объединение двух совокупностей A и B образует новую совокупность, состоящую из всех элементов, которые принадлежат хотя бы одной из этих совокупностей. Обозначается символом ∪.

Пересечение: пересечение двух совокупностей A и B образует новую совокупность, состоящую из всех элементов, которые принадлежат одновременно и A, и B. Обозначается символом ∩.

Разность: разность двух совокупностей A и B образует новую совокупность, состоящую из всех элементов, которые принадлежат A, но не принадлежат B. Обозначается символом \.

Операции над совокупностями обладают рядом свойств, которые облегчают и упрощают работу с ними:

• Коммутативность: операции объединения и пересечения коммутативны, то есть порядок совокупностей не влияет на результат. Например, A ∪ B = B ∪ A.
• Ассоциативность: операции объединения и пересечения ассоциативны, то есть результат не зависит от скобочной структуры. Например, (A ∪ B) ∪ C = A ∪ (B ∪ C).
• Идемпотентность: операции объединения и пересечения идемпотентны, то есть повторное применение операции не меняет результат. Например, A ∪ A = A и A ∩ A = A.
• Распределительность: операция пересечения дистрибутивна относительно операции объединения и наоборот. Например, A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
• Пустое множество: пустое множество является нейтральным элементом для операции объединения, то есть A ∪ ∅ = A. Пустое множество также является абсорбирующим элементом для операции пересечения, то есть A ∩ ∅ = ∅.

Понимание операций над совокупностями и их свойств позволяет эффективно работать с математическими моделями и решать разнообразные задачи, связанные с совокупностями.

Связь совокупностей с другими математическими понятиями

Совокупность в математике тесно связана с другими понятиями, которые помогают ее определить и применять в различных математических задачах.

Одним из основных понятий, связанных со совокупностью, является множество. Множество представляет собой совокупность элементов, объединенных общим свойством. Совокупность может быть представлена как одно множество, содержащее все элементы, или как объединение нескольких множеств.

Другим важным понятием, связанным со совокупностью, является подмножество. Подмножество — это часть множества, которая содержит только некоторые из его элементов. В контексте совокупности, подмножество может описывать группу элементов, которые удовлетворяют определенным условиям или критериям.

Совокупности также связаны с понятием отношения. Отношение определяет связь между элементами двух или более множеств. В контексте совокупности, отношение может помочь определить, какие элементы принадлежат совокупности и как они связаны между собой.

Еще одним понятием, связанным со совокупностью, является функция. Функция определяет соответствие между элементами одного множества и элементами другого множества. В контексте совокупности, функция может помочь определить, какие элементы принадлежат совокупности и как они связаны с другими элементами.

Таким образом, совокупность в математике имеет связь с другими важными понятиями, такими как множество, подмножество, отношение и функция. Эти понятия помогают определить и использовать совокупности в различных математических задачах.

Роль совокупностей в решении прикладных задач

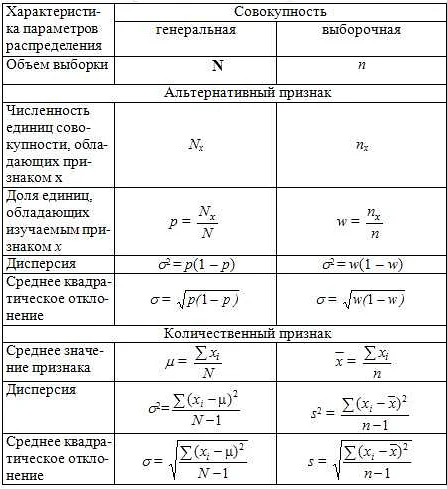
Совокупности играют важную роль в решении прикладных математических задач. Они позволяют описывать и анализировать множество объектов или явлений, которые встречаются в реальном мире.

В прикладных задачах совокупности могут использоваться для сбора и структурирования данных. Например, при анализе результатов опроса или исследования, данные часто группируются в совокупности по различным критериям. Это позволяет исследователям получить общую картину и выявить закономерности.

Совокупности также используются для определения вероятностей и статистических характеристик. Например, в экономике совокупности могут использоваться для моделирования поведения рынка и прогнозирования будущих тенденций.

Кроме того, совокупности могут быть полезны для решения задач в области оптимизации. Например, при планировании производства или распределении ресурсов, совокупности позволяют учесть все необходимые факторы и принять оптимальные решения.

Исследование и использование совокупностей в решении прикладных задач помогает улучшить точность прогнозов, оптимизировать процессы и принять обоснованные решения на основе имеющихся данных. Поэтому понимание и применение совокупностей является важной компетенцией в различных областях науки и промышленности.