Чем занимается математическая статистика
Содержимое
- 1 Чем занимается математическая статистика
- 1.1 Математическая статистика: основные понятия и методы
- 1.2 Что такое математическая статистика
- 1.3 Роль математической статистики в науке и промышленности
- 1.4 Основные понятия математической статистики
- 1.5 Виды данных в математической статистике
- 1.6 Методы сбора данных в математической статистике
- 1.7 Вопрос-ответ:
- 1.8 Описательная статистика: анализ и интерпретация данных
- 1.9 Видео по теме:
Математическая статистика — это наука, которая занимается сбором, анализом и интерпретацией данных для принятия решений на основе математических методов. Она помогает понять статистические закономерности и прогнозировать вероятности событий на основе имеющихся данных. Математическая статистика используется в различных областях, включая экономику, финансы, медицину, социологию и многое другое.
Математическая статистика является разделом статистики, который использует математические методы и модели для анализа данных. Ее основная цель состоит в том, чтобы извлекать информацию и делать выводы на основе имеющихся данных. Математическая статистика широко применяется в различных областях, включая науку, инженерию, экономику и медицину.
Основные понятия математической статистики включают в себя понятия случайной величины, выборки, вероятностных распределений и статистических оценок. Случайная величина представляет собой числовую характеристику случайного эксперимента, такую как количество выпавших орлов при многократном подбрасывании монеты. Выборка представляет собой подмножество случайных величин из генеральной совокупности. Вероятностное распределение определяет вероятности различных значений случайной величины. Статистическая оценка позволяет делать выводы о генеральной совокупности на основе данных из выборки.
Методы математической статистики включают в себя описательную статистику, которая предоставляет сводные характеристики данных, такие как среднее значение или стандартное отклонение. Другие методы включают проверку статистических гипотез, построение доверительных интервалов и анализ регрессии. Проверка статистических гипотез позволяет делать выводы о параметрах генеральной совокупности на основе данных из выборки. Построение доверительных интервалов позволяет оценить неопределенность статистических оценок. Анализ регрессии позволяет исследовать зависимости между переменными и строить прогнозы на основе этих зависимостей.
Математическая статистика играет важную роль в современной науке и позволяет исследователям делать выводы на основе данных. Она предоставляет инструменты для анализа и интерпретации данных, а также для построения статистических моделей. Знание основных понятий и методов математической статистики является важным для всех, кто работает с данными и стремится делать обоснованные выводы на их основе.
Математическая статистика: основные понятия и методы

Основными понятиями в математической статистике являются выборка, статистический ряд, вероятность, математическое ожидание, дисперсия, корреляция и регрессия. Выборка представляет собой набор случайных наблюдений, взятых из некоторого исследуемого множества. Статистический ряд — это упорядоченный набор значений в выборке с указанием их частоты появления. Вероятность определяет степень возможности наступления определенного события. Математическое ожидание и дисперсия характеризуют среднюю величину и разброс случайной величины. Корреляция и регрессия используются для анализа зависимостей между случайными величинами.
Для обработки данных в математической статистике применяются различные методы. Одним из основных методов является описательная статистика, которая позволяет суммировать, описывать и интерпретировать имеющиеся данные. Она включает в себя вычисление средних значений, дисперсий, стандартных отклонений и других характеристик выборки.
Для проверки статистических гипотез используются статистические тесты. Они позволяют определить, насколько вероятно получить наблюдаемые данные при условии, что некоторая гипотеза верна. Статистические тесты могут быть параметрическими или непараметрическими, в зависимости от предположений о распределении данных.
Математическая статистика также занимается построением статистических моделей. Статистическая модель описывает зависимости между переменными и позволяет прогнозировать значения одной переменной на основе других. Методы построения статистических моделей включают линейную и нелинейную регрессию, временные ряды, анализ выживаемости и др.
Математическая статистика имеет широкое применение в различных областях, включая экономику, финансы, медицину, социологию, биологию и многое другое. Она позволяет делать выводы на основе данных и принимать обоснованные решения на основе статистического анализа.
Что такое математическая статистика

Математическая статистика является важным инструментом для исследования данных в различных областях, таких как экономика, социология, медицина, физика и многое другое. Она помогает нам понять статистическую значимость результатов и определить, насколько они достоверны.
Основные понятия и методы математической статистики включают:
- Выборка и генеральная совокупность: выборка — это подмножество данных, которое мы анализируем, а генеральная совокупность — это полный набор данных, из которого была взята выборка.
- Меры центральной тенденции: такие как среднее значение, медиана и мода, позволяют нам описать типичное значение в выборке.
- Меры изменчивости: такие как дисперсия и стандартное отклонение, помогают оценить степень разброса данных в выборке.
- Распределения вероятностей: такие как нормальное распределение, позволяют нам описать вероятностные характеристики данных и проводить статистические тесты.
- Статистические тесты: такие как t-тест, анализ дисперсии и регрессионный анализ, используются для проверки гипотез и выявления связей между переменными.
Математическая статистика позволяет нам использовать математические методы и модели для анализа данных и принятия обоснованных выводов. Она является неотъемлемой частью современной науки и позволяет нам получать новые знания и делать предсказания на основе имеющихся данных.
Роль математической статистики в науке и промышленности
В науке математическая статистика позволяет проводить эксперименты, собирать данные и статистически анализировать полученные результаты. Она помогает исследователям проверять гипотезы, делать выводы и формулировать законы и теории на основе имеющихся данных. Математическая статистика также позволяет оценивать степень достоверности полученных результатов и определять их статистическую значимость.
В промышленности математическая статистика используется для улучшения процессов производства и оптимизации бизнес-процессов. Она помогает анализировать и интерпретировать данные, полученные в ходе производства, и принимать решения на основе этих данных. Математическая статистика позволяет выявлять причинно-следственные связи между различными переменными, определять факторы, влияющие на производительность и качество продукции, а также предсказывать будущие результаты.
Основные понятия и методы математической статистики, такие как статистические тесты, регрессионный анализ, корреляционный анализ и др., широко применяются в различных областях науки и промышленности, включая экономику, медицину, социологию, физику, инженерию и многие другие.
Примеры применения математической статистики в науке и промышленности:
| Оценка эффективности нового лекарственного препарата |
| Анализ климатических данных для прогнозирования погоды |
| Определение факторов, влияющих на рост продаж |
| Статистическое моделирование для прогнозирования трендов в экономике |
Таким образом, математическая статистика играет важную роль в науке и промышленности, помогая исследователям и бизнесменам принимать обоснованные решения на основе анализа данных и статистических методов.
Основные понятия математической статистики

Основные понятия математической статистики включают в себя:
Выборка: это набор данных, полученных из исследуемой генеральной совокупности. Исследователи часто не имеют возможности изучить всю генеральную совокупность, поэтому они берут выборку для проведения статистического анализа.
Параметрические и непараметрические методы: параметрические методы статистики основываются на предположении о форме вероятностного распределения данных, например, нормального распределения. Непараметрические методы не делают такого предположения и позволяют анализировать данные, которые не удовлетворяют предположениям о распределении.
Математическое ожидание: среднее значение распределения исследуемой случайной величины. Математическое ожидание является одной из мер центральной тенденции и используется для описания среднего значения выборки.
Дисперсия: мера разброса данных относительно их среднего значения. Дисперсия позволяет оценить, насколько значения отклоняются от среднего и как они распределены вокруг него.
Статистические тесты: статистические тесты позволяют проверить гипотезы о различиях между группами данных или о влиянии факторов на данные. Они основаны на применении статистических моделей и позволяют делать выводы на основе статистической значимости.
Доверительный интервал: интервал, в котором с определенной вероятностью содержится истинное значение параметра генеральной совокупности. Доверительный интервал позволяет оценить неопределенность параметра на основе выборки и указать на то, как точно можно сделать выводы на основе этих данных.
Основные понятия математической статистики являются основой для проведения статистического анализа данных. Они позволяют исследователям делать выводы и принимать решения на основе данных, а также оценивать неопределенность и риски своих выводов.
Виды данных в математической статистике

Математическая статистика изучает различные виды данных, которые могут быть получены из исследований и наблюдений. В зависимости от природы данных и их характеристик, применяются различные методы и подходы для их анализа и интерпретации.
В математической статистике выделяют следующие виды данных:
Вид данныхОписание
| Количественные данные | Представляют числовые значения и могут быть измерены с определенной точностью. Например, возраст, вес, рост. |
| Качественные данные | Представляют категории или качественные характеристики, которые не могут быть измерены числовыми значениями. Например, пол, цвет глаз, национальность. |
| Дискретные данные | Представляют отдельные значения, которые могут быть перечислены или посчитаны. Например, количество детей в семье, количество аварий на дорогах в течение года. |
| Непрерывные данные | Представляют значения, которые находятся в определенном диапазоне и могут быть измерены с любой точностью. Например, время, температура, длина. |
Корректный выбор метода анализа данных в математической статистике зависит от типа данных, их распределения, объема выборки и поставленных задач. Каждый вид данных требует своего подхода и специфических методов статистического анализа.
Методы сбора данных в математической статистике
Математическая статистика включает в себя различные методы сбора данных, которые позволяют получить информацию о случайной величине или наблюдаемом явлении. Важно выбрать подходящий метод сбора данных, чтобы полученная выборка была репрезентативной и позволяла делать статистические выводы о всей генеральной совокупности.
Основные методы сбора данных в математической статистике включают:
- Репрезентативная выборка. Этот метод предполагает случайное выборку из генеральной совокупности, чтобы получить данные, которые наиболее точно отражают характеристики всей генеральной совокупности. Репрезентативная выборка может быть простой случайной выборкой, стратифицированной выборкой или кластерной выборкой.
- Опросы. Опросы являются одним из самых распространенных методов сбора данных в математической статистике. Они могут быть проведены путем личного интервью, телефонного опроса, письменного опроса или веб-опроса. Опросы позволяют получить информацию от респондентов напрямую, что позволяет изучать их мнения, предпочтения и поведение.
- Наблюдение. Метод наблюдения предполагает наблюдение за явлениями или событиями в естественной среде без вмешательства. Наблюдение может быть структурированным, когда исследователь следит за определенными параметрами, или неструктурированным, когда исследователь наблюдает явления без предварительного определения параметров.
- Эксперименты. В экспериментах исследователи манипулируют независимыми переменными, чтобы изучить их влияние на зависимые переменные. Эксперименты позволяют устанавливать причинно-следственные связи и делать выводы о влиянии определенных факторов на исследуемые явления.
- Анализ существующих данных. Иногда исследователи могут использовать уже существующие данные для анализа. Это могут быть данные, полученные в предыдущих исследованиях, архивные данные или данные, собранные другими организациями. Анализ существующих данных позволяет проводить ретроспективные исследования, а также исследования на основе больших объемов данных.
Выбор конкретного метода сбора данных зависит от целей исследования, доступных ресурсов и ограничений. Важно учитывать преимущества и недостатки каждого метода, чтобы получить достоверные и репрезентативные результаты и сделать статистически обоснованные выводы.
Вопрос-ответ:
Какие основные понятия изучает математическая статистика?
Математическая статистика изучает различные понятия, связанные с сбором, анализом и интерпретацией данных. Основные понятия включают в себя выборку, статистический показатель, вероятностное распределение, гипотезу, статистическую модель и многое другое.
Какие методы применяются в математической статистике?
В математической статистике применяется ряд различных методов. Некоторые из них включают методы описательной статистики, методы статистического вывода, методы проверки гипотез, методы регрессионного анализа и методы анализа временных рядов.
Какова роль математической статистики в науке и исследованиях?
Математическая статистика играет важную роль в науке и исследованиях. Она позволяет проводить анализ данных, делать выводы на основе имеющихся данных, проверять гипотезы и строить статистические модели. Без математической статистики было бы очень сложно проводить объективные и надежные исследования.
Каким образом математическая статистика помогает в принятии решений?
Математическая статистика помогает в принятии решений путем анализа данных и проведения статистического вывода. Она позволяет определить вероятность различных событий и оценить степень уверенности в принимаемых решениях. Математическая статистика также помогает выявить взаимосвязи между различными переменными и предсказать будущие значения.
Описательная статистика: анализ и интерпретация данных

Одним из основных понятий в описательной статистике является понятие «переменная». Переменная — это характеристика, которая может принимать различные значения. Например, возраст, рост, вес — все это переменные.
Для описания данных мы используем такие показатели, как среднее значение, медиана, мода, дисперсия, стандартное отклонение и другие. Среднее значение показывает среднюю величину переменной в выборке, медиана — значение, разделяющее выборку пополам, мода — значение, которое встречается наиболее часто.
Описательная статистика также позволяет нам оценить разброс данных. Для этого мы используем такие показатели, как дисперсия и стандартное отклонение. Дисперсия показывает, насколько переменная распределена вокруг своего среднего значения, а стандартное отклонение — меру разброса данных.
Определение формы распределения данных также является важным аспектом описательной статистики. Для этого мы используем графические методы, такие как гистограмма, диаграмма рассеяния и другие.
Интерпретация данных является неотъемлемой частью описательной статистики. Она позволяет нам делать выводы и сделать заключения на основе имеющихся данных. Например, мы можем сравнивать различные группы данных, выявлять различия и сходства между ними, а также исследовать связи и зависимости между переменными.
В целом, описательная статистика является важным инструментом для анализа данных. Она позволяет нам систематизировать информацию, выявлять основные характеристики данных и делать выводы на основе имеющихся фактов. Благодаря описательной статистике мы можем лучше понять и интерпретировать данные, а также использовать их для принятия решений и обоснования выводов.


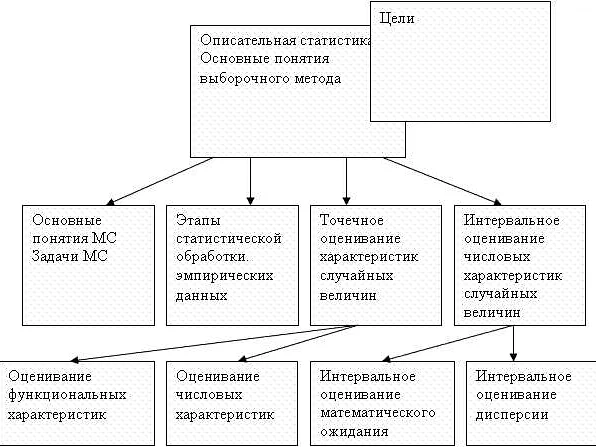


Математическая статистика – это наука, которая изучает методы анализа и интерпретации данных для принятия обоснованных выводов и решений. В основе этой дисциплины лежит математическая теория вероятностей, которая позволяет строить модели и прогнозировать различные события. Одна из основных задач математической статистики – определение характеристик выборки, таких как среднее значение, дисперсия и корреляция. Эти параметры позволяют оценить, насколько выборка отражает генеральную совокупность и какие закономерности могут быть выявлены. Для достижения этой цели математическая статистика использует различные методы, такие как метод максимального правдоподобия, метод наименьших квадратов, критерии согласия и доверительные интервалы. Они позволяют проверить гипотезы о параметрах генеральной совокупности и делать статистические выводы. Одним из важных аспектов математической статистики является также анализ регрессии и корреляционный анализ. Они позволяют установить зависимости между переменными и построить математические модели для прогнозирования. В целом, математическая статистика играет ключевую роль в научных исследованиях, анализе данных и принятии решений в различных областях, таких как экономика, медицина, социология и многие другие. Она позволяет выявлять закономерности, делать статистически обоснованные выводы и прогнозировать будущие события.