Что такое методы математической статистики
Содержимое
- 1 Что такое методы математической статистики
- 1.1 Понятие математической статистики
- 1.2 Применение математической статистики
- 1.3 Основные принципы математической статистики
- 1.4 Методы сбора данных в математической статистике
- 1.5 Методы анализа данных в математической статистике
- 1.6 Видео по теме:
- 1.7 Вопрос-ответ:
- 1.7.0.1 Что такое методы математической статистики?
- 1.7.0.2 Какие основные принципы лежат в основе методов математической статистики?
- 1.7.0.3 Какие области применения имеют методы математической статистики?
- 1.7.0.4 Какие методы математической статистики используются для проверки гипотез?
- 1.7.0.5 Что такое методы математической статистики?
- 1.7.0.6 Какие основные принципы лежат в основе методов математической статистики?
- 1.7.0.7 Каким образом методы математической статистики применяются в реальной жизни?
- 1.8 Виды статистических выводов
- 1.9 Применение математической статистики в различных областях
Методы математической статистики — это совокупность математических методов и подходов, применяемых для анализа данных, извлечения статистических выводов и принятия решений на основе этих данных. Эта область науки позволяет оценивать параметры распределений, проверять гипотезы, строить прогнозы и моделировать случайные процессы. Понимание методов математической статистики является ключевым для решения различных задач в науке, экономике, медицине и других областях, где требуется анализ данных и статистическое обоснование решений.
Математическая статистика – это раздел математики, который изучает методы и процедуры анализа данных с целью выявления закономерностей и получения выводов на основе вероятностных моделей. Она является одним из основных инструментов для работы с данными в различных областях, включая науку, технику, экономику и социологию.
Применение методов математической статистики позволяет сделать выводы о генеральной совокупности на основе информации, полученной из выборки. Она позволяет извлечь полезную информацию из огромного объема данных и выявить основные закономерности. Статистические методы позволяют определить характеристики распределения данных, оценить параметры моделей, проверить статистические гипотезы и сделать прогнозы.
Основными принципами математической статистики являются выборочное исследование и статистическое выводы на основе вероятностных моделей. Выборочное исследование предусматривает изучение характеристик выборки и их экстраполяцию на генеральную совокупность. Статистический вывод — это процесс сделать выводы и принять решения на основе статистических данных и методов.
Методы математической статистики используются для решения различных задач, таких как анализ и интерпретация данных, проведение экспериментов, моделирование и прогнозирование. Они используются для обработки и интерпретации результатов научных исследований, а также для принятия решений на основе доступных данных. Знание и применение методов математической статистики позволяют получить объективные оценки, уменьшить ошибку и риски и принять обоснованные решения.
Понятие математической статистики
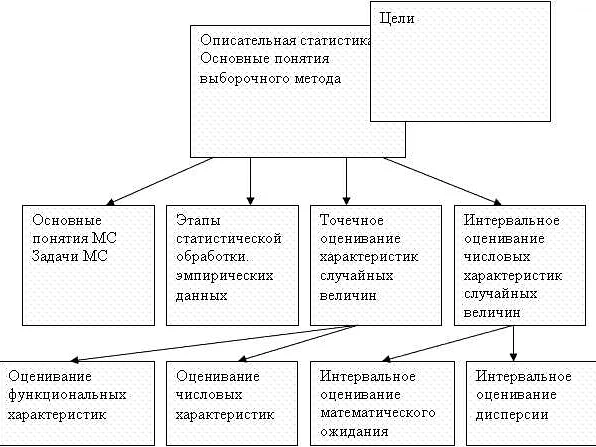
Основная цель математической статистики – изучение случайных процессов и явлений на основе имеющейся информации. Этот раздел математики позволяет ученым делать выводы и прогнозы на основе собранных данных, а также проверять гипотезы и решать различные задачи, связанные с вероятностными моделями.
Математическая статистика включает в себя различные методы, такие как описательная статистика, статистические выводы, регрессионный анализ, анализ временных рядов и другие. Она активно применяется в различных областях науки и практической деятельности, таких как экономика, финансы, социология, медицина и др.
Основные принципы математической статистики включают сбор данных, их анализ, построение статистических моделей, проверку гипотез и выводы на основе полученных результатов. Одним из ключевых принципов является использование вероятностных моделей для описания и анализа случайных явлений.
Математическая статистика играет важную роль в научном и практическом исследовании, позволяя получать объективные результаты и делать обоснованные выводы на основе имеющихся данных.
Применение математической статистики

Математическая статистика имеет широкое применение в различных областях науки и практике. Ее основные принципы и методы позволяют решать задачи, связанные с анализом данных, проверкой гипотез, оценкой параметров и прогнозированием.
Одной из сфер применения математической статистики является исследование социально-экономических явлений. С ее помощью можно анализировать данные о доходах населения, уровне безработицы, инфляции и других показателях, чтобы выявить закономерности и тенденции развития. На основе статистических данных можно принимать решения о разработке и реализации социально-экономической политики.
Математическая статистика также применяется в медицине для анализа клинических исследований. Она позволяет оценить эффективность новых лекарственных препаратов, определить факторы риска различных заболеваний и разработать стратегии их профилактики. Статистические методы помогают принимать обоснованные решения в области здравоохранения и повышать качество медицинского обслуживания.
В финансовой сфере математическая статистика используется для анализа финансовых рынков, прогнозирования цен на акции и другие финансовые инструменты. Статистические методы позволяют определить риски и доходность инвестиционных портфелей, разработать стратегии управления рисками и принять обоснованные инвестиционные решения.
Математическая статистика находит применение в различных научных исследованиях, включая физику, биологию, психологию и социологию. Она позволяет анализировать экспериментальные данные, проверять гипотезы, оценивать параметры и строить математические модели. Статистические методы помогают ученым извлекать информацию из сложных и многообразных данных и делать выводы на основе статистической значимости.
Наконец, математическая статистика применяется в машинном обучении и искусственном интеллекте. Статистические методы позволяют обрабатывать и анализировать большие объемы данных, делать прогнозы и принимать решения на основе статистических закономерностей. Они являются основой для разработки алгоритмов машинного обучения и создания интеллектуальных систем.
Таким образом, математическая статистика играет важную роль в различных областях человеческой деятельности, предоставляя надежные инструменты для анализа данных, принятия обоснованных решений и развития науки и технологий.
Основные принципы математической статистики
1. Случайность: В основе математической статистики лежит предположение о случайности данных. Данные считаются случайными в том смысле, что они представляют собой результат случайного процесса или эксперимента, и их значения могут варьироваться. Использование методов математической статистики позволяет извлечь информацию из случайных данных и сделать выводы о всей генеральной совокупности.
2. Выборка: В математической статистике данные собираются путем проведения выборки. Выборка представляет собой подмножество данных из генеральной совокупности. От выборки зависит точность и достоверность статистических выводов. Правильное формирование выборки, учет ее размера и методов отбора являются важными принципами математической статистики.
3. Статистические оценки: Математическая статистика предоставляет методы для оценки неизвестных параметров генеральной совокупности на основе выборки. Статистические оценки позволяют получить приближенные значения параметров и определить их точность. Кроме того, на основе статистических оценок можно проводить статистические сравнения и тестирование гипотез.
4. Вероятность: Вероятностный подход является ключевым в математической статистике. Он позволяет формализовать статистические модели и методы с помощью понятий вероятности и случайных величин. Вероятностные модели используются для описания случайных данных и для построения статистических выводов.
5. Интерпретация результатов: Один из важных принципов математической статистики заключается в правильной интерпретации полученных статистических результатов. Это включает в себя объяснение статистических выводов и их применимости к реальным ситуациям. Интерпретация статистических результатов должна быть основана на теоретических знаниях и понимании предметной области исследования.
Основные принципы математической статистики позволяют проводить анализ данных, делать выводы о генеральной совокупности и принимать решения на основе статистических закономерностей. Правильное применение этих принципов позволяет улучшить качество и надежность статистических выводов и сделать более точные решения в различных областях знаний и научных исследований.
Методы сбора данных в математической статистике
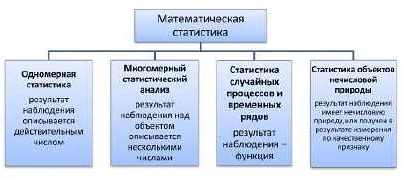
В математической статистике существует несколько основных методов сбора данных. Один из самых распространенных методов — опрос. Опрос предполагает проведение анкетирования или интервьюирования, в ходе которого исследователь задает определенные вопросы и получает ответы от респондентов. Опрос может быть структурированным, когда вопросы заранее подготовлены и формализованы, или неструктурированным, когда исследователь задает вопросы по ходу беседы.
Еще один метод сбора данных — эксперимент. Эксперимент предполагает контролируемое воздействие на объект исследования с целью изучения его реакции. Эксперимент может проводиться в лабораторных условиях или на практике, в зависимости от предмета исследования.
Также в математической статистике используется метод наблюдения. Наблюдение предполагает фиксацию и изучение реальных процессов и явлений, без вмешательства исследователя. Наблюдение может быть непосредственным, когда исследователь сам непосредственно наблюдает за объектом, или опосредованным, когда данные собираются через различные устройства и системы.
Кроме того, в математической статистике используются методы регистрации данных. Регистрация предполагает сбор данных при помощи различных приборов и устройств: счетчиков, датчиков, камер и т.д. Такой метод позволяет получить точные и объективные данные.
Важно отметить, что выбор метода сбора данных зависит от целей исследования, доступности ресурсов, а также характера исследуемого объекта. Каждый метод имеет свои преимущества и ограничения, поэтому исследователь должен внимательно подходить к выбору метода и учитывать его особенности.
Методы анализа данных в математической статистике
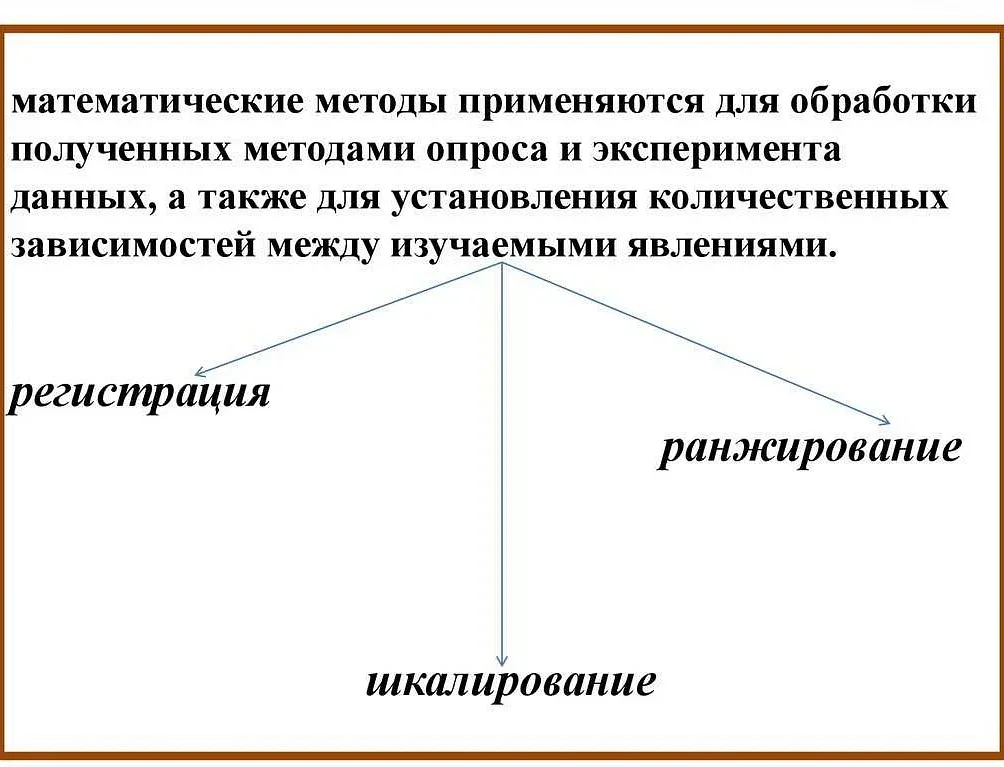
Одним из основных методов анализа данных является описательная статистика. Она включает в себя различные показатели, такие как среднее арифметическое, медиана, мода, дисперсия и стандартное отклонение. Описательная статистика позволяет получить представление о распределении данных и выявить основные характеристики выборки.
Для более глубокого анализа данных применяются регрессионный анализ и корреляционный анализ. Регрессионный анализ позволяет определить зависимость между двумя переменными и построить уравнение регрессии. Корреляционный анализ позволяет оценить степень связи между двумя переменными и определить коэффициент корреляции.
Для проверки гипотез о параметрах генеральной совокупности используются статистические тесты. Наиболее известные из них — t-тест Стьюдента и z-тест. Они позволяют определить, насколько выборочные данные отличаются от ожидаемых значений и делать выводы о статистической значимости этих различий.
Помимо приведенных методов, в математической статистике существуют и другие методы анализа данных, такие как анализ дисперсии, факторный анализ, временные ряды и другие. Все они имеют свои особенности и применяются в различных ситуациях для более глубокого и точного анализа данных.
МетодОписание
| Описательная статистика | Позволяет получить основные характеристики выборки |
| Регрессионный анализ | Определяет зависимость между переменными и строит уравнение регрессии |
| Корреляционный анализ | Оценивает степень связи между переменными и определяет коэффициент корреляции |
| Статистические тесты | Позволяют проверить гипотезы о параметрах генеральной совокупности |
Все эти методы анализа данных являются важными инструментами математической статистики и позволяют сделать выводы на основе выборочных данных. Они широко применяются в различных областях, таких как экономика, медицина, социология и другие, для анализа и интерпретации данных.
Видео по теме:
Вопрос-ответ:
Что такое методы математической статистики?
Методы математической статистики — это совокупность математических методов и инструментов, которые используются для анализа статистических данных и извлечения из них полезной информации. Они позволяют провести объективное и точное исследование, оценку и прогнозирование явлений в различных областях науки и практики.
Какие основные принципы лежат в основе методов математической статистики?
Основные принципы методов математической статистики включают сбор и обработку данных, их описательный анализ, построение статистических моделей и проверка их адекватности, а также статистическую оценку и проверку гипотез. Эти принципы позволяют выявить закономерности и зависимости в данных, сделать выводы о статистической значимости полученных результатов и сделать прогнозы о будущих явлениях.
Какие области применения имеют методы математической статистики?
Методы математической статистики находят применение во многих областях знания и практики, включая экономику, финансы, медицину, биологию, психологию, социологию, астрономию и физику. Они используются для анализа и прогнозирования экономических показателей, изучения эффективности лекарственных препаратов, исследования влияния различных факторов на поведение людей или оценки вероятности наступления определенных событий.
Какие методы математической статистики используются для проверки гипотез?
Для проверки гипотез в методах математической статистики используются различные статистические тесты. Например, t-тест используется для проверки значимости различий между средними значениями двух выборок, а анализ дисперсии (ANOVA) — для проверки значимости различий между средними значениями трех или более выборок. С помощью этих тестов можно определить, являются ли различия между выборками статистически значимыми или они могут быть случайными.
Что такое методы математической статистики?
Методы математической статистики представляют собой совокупность математических и статистических методов, используемых для анализа данных и извлечения информации о случайных явлениях.
Какие основные принципы лежат в основе методов математической статистики?
Основными принципами методов математической статистики являются статистический вывод, оценивание параметров, проверка статистических гипотез и анализ регрессии.
Каким образом методы математической статистики применяются в реальной жизни?
Методы математической статистики широко применяются в различных областях, таких как экономика, медицина, физика, социология и другие. Они позволяют анализировать и интерпретировать данные, прогнозировать будущие события и принимать научно обоснованные решения.
Виды статистических выводов

В математической статистике существует несколько видов статистических выводов, которые позволяют делать заключения о генеральной совокупности на основе выборки. Рассмотрим основные из них:
1. Параметрические статистические выводы: в этом случае предполагается, что генеральная совокупность имеет определенное распределение вероятностей с заданными параметрами. На основе выборки вычисляются оценки параметров распределения и строятся интервальные оценки для этих параметров. Данный вид выводов основывается на применении математических моделей и требует соответствия выборки определенным условиям.
2. Непараметрические статистические выводы: в этом случае не делается предположений о виде распределения генеральной совокупности. Вместо этого используются ранги или порядковые значения данных. Непараметрические методы основываются на знаках, рангах, перестановках и других статистических критериях, которые не требуют определения параметров распределения. Этот вид выводов более гибкий и применим в случаях, когда параметрические методы не могут быть использованы.
3. Байесовские статистические выводы: основаны на применении теоремы Байеса, которая позволяет обновлять априорные вероятности на основе новой информации. Вместо точечных оценок параметров используются апостериорные распределения. Байесовские методы могут быть полезны в случаях, когда у нас есть некоторые априорные знания о генеральной совокупности или когда нам нужно учесть неопределенность в данных.
Выбор конкретного метода статистического вывода зависит от специфики задачи и доступных данных. Важно учитывать ограничения и предпосылки каждого метода, чтобы правильно интерпретировать полученные результаты.
Применение математической статистики в различных областях

В экономике математическая статистика применяется для анализа финансовых данных, моделирования экономических процессов, определения тенденций и прогнозирования развития рынков. Она позволяет выявить закономерности в статистических данных, оценить степень влияния различных факторов на экономические показатели и принять обоснованные решения в сфере бизнеса и финансов.
В медицине математическая статистика помогает анализировать результаты клинических исследований, определять эффективность лечения, прогнозировать развитие заболеваний и оценивать риски для пациентов. С ее помощью врачи могут выявить взаимосвязи между различными факторами и заболеваниями, определить эффективность лекарственных препаратов и проводить статистические исследования для разработки новых методов лечения.
В социологии математическая статистика используется для анализа социальных явлений и процессов, определения тенденций и закономерностей в обществе. Она позволяет проводить опросы и исследования, анализировать социальные данные, оценивать общественное мнение и прогнозировать социальные процессы. С ее помощью можно выявить взаимосвязи между различными социальными факторами и предсказывать развитие общества.
В науке математическая статистика используется для анализа результатов экспериментов, проверки гипотез, моделирования и прогнозирования. Она позволяет выявить статистически значимые зависимости и закономерности, оценить точность и достоверность полученных результатов, а также проводить статистические исследования для развития новых научных теорий и концепций.
Таким образом, математическая статистика находит применение в различных областях, где требуется анализ, моделирование, прогнозирование и принятие решений на основе статистических данных. Она является мощным инструментом для извлечения информации из больших объемов данных, выявления закономерностей и прогнозирования различных явлений и процессов.
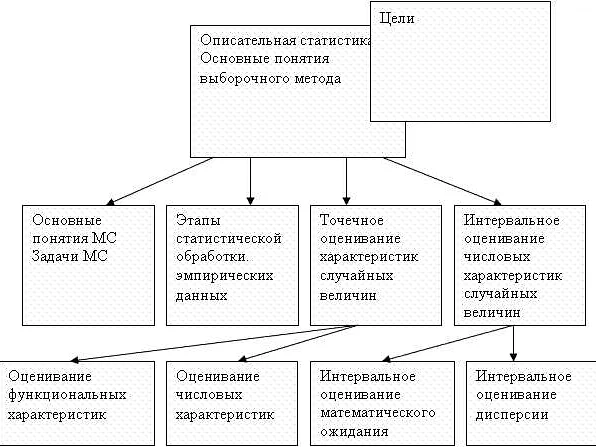




Математическая статистика – это наука, которая помогает нам понять и объяснить различные явления и закономерности в наших данных. Она является неотъемлемой частью современной науки и технологий, ведь все, что мы делаем, основывается на данных. Методы математической статистики широко применяются во многих областях, от экономики и медицины до физики и машинного обучения. Эти методы позволяют нам извлекать полезную информацию из данных, проводить статистические тесты гипотез, строить прогнозы и принимать обоснованные решения. Основные принципы математической статистики включают сбор и описание данных, их анализ и интерпретацию. Важным аспектом является выбор подходящей модели для описания данных и использование статистических методов для проверки гипотез и получения выводов. Математическая статистика помогает нам понять вероятностные закономерности и связи в данных, а также оценить надежность и точность наших результатов. Она требует точности и аккуратности в работе с данными, чтобы избежать ошибок и искажений. В заключение, методы математической статистики являются мощным инструментом для анализа данных и принятия обоснованных решений. Они широко применяются в различных областях и помогают нам найти закономерности и понять мир вокруг нас.
Статья очень интересная и полезная! Я всегда была заинтересована в математике и статистике, но никогда не смогла разобраться в их методах и принципах. Эта статья прекрасно объясняет основные понятия и применение математической статистики. Математическая статистика – это наука, которая изучает методы сбора, описания, анализа и интерпретации данных. Она играет важную роль во многих областях, включая экономику, медицину, социологию и многие другие. Статья подробно описывает основные принципы математической статистики, такие как выборка, распределение вероятностей, статистическая оценка и проверка гипотез. Она также показывает, как эти принципы могут быть применены на практике. Особенно мне понравился пример использования методов математической статистики для анализа данных о заболеваемости в разных регионах. Это пример, который помогает лучше понять, как можно использовать эти методы для получения полезной информации. Статья написана очень понятно и доступно. Я узнала много нового о методах математической статистики и теперь чувствую себя более уверенно в этой области. Спасибо автору за такую информативную статью!