Что такое числительное в математике

Числительное в математике – это особый тип чисел, который используется для обозначения количества или порядка предметов или явлений. В данной статье мы рассмотрим основные понятия и свойства числительных, а также их применение в математике и повседневной жизни.

В математике числительное – это понятие, которое используется для обозначения количества или порядка объектов. Числительные являются одной из основных составляющих числовой системы и позволяют нам оперировать с числами и выполнять различные математические операции.

Одно из основных свойств числительных – это их классификация на кардинальные, порядковые и множественные. Кардинальные числительные обозначают количество объектов, порядковые – их порядок, а множественные – количество составляющих элементов.

Примеры числительных в математике могут быть разными. Например, в кардинальном числе «три» обозначается количество объектов: «у меня есть три яблока». В порядковом числе «пятый» обозначается позиция объекта в ряду: «он занял пятую строчку». А в множественном числе «четыре» обозначается количество составляющих элементов: «у нас было четыре команды на соревнованиях».

Что такое числительное в математике?

Числительные включают в себя различные типы чисел, такие как натуральные числа, целые числа, рациональные числа и действительные числа. Натуральные числа – это числа, которые используются для обозначения количества предметов или явлений, начиная с единицы и увеличиваясь на единицу. Целые числа включают в себя натуральные числа, ноль и отрицательные числа. Рациональные числа – это числа, которые могут быть представлены в виде дроби, где числитель и знаменатель являются целыми числами. Действительные числа – это числа, которые могут быть представлены на числовой оси и включают в себя как рациональные числа, так и иррациональные числа.

Числительные имеют свои специфические свойства, которые позволяют выполнять различные операции над ними. Например, натуральные числа можно складывать, вычитать, умножать и делить. Целые числа можно складывать, вычитать и умножать, а также выполнять операции деления и нахождения остатка от деления. Рациональные числа можно складывать, вычитать, умножать и делить, а также находить их противоположные числа и абсолютные значения. Действительные числа можно складывать, вычитать, умножать и делить, а также извлекать их квадратные корни и находить их противоположные числа и абсолютные значения.

Примеры числительных в математике включают следующие числа: 1, 2, 3, 4, 5 (натуральные числа), 0, -1, -2, -3, -4 (целые числа), 1/2, 3/4, 2/3, 5/6 (рациональные числа), 1.5, -2.7, 3.14 (действительные числа).

Видео по теме:

Основные свойства числительного

Основные свойства числительного включают:

1. Сложение и вычитание числительных: числительные можно складывать и вычитать, чтобы получить новое числительное. Например, 4 + 3 = 7 и 10 — 2 = 8.
2. Умножение и деление числительных: числительные можно умножать и делить, чтобы получить новое числительное. Например, 5 × 2 = 10 и 16 ÷ 4 = 4.
3. Возведение в степень: числительное можно возвести в степень, чтобы получить новое числительное. Например, 2^3 = 8 и 10^2 = 100.
4. Сравнение числительных: числительные можно сравнивать между собой, чтобы определить, какое из них больше или меньше. Например, 7 > 5 и 12 < 15.
5. Использование числительных в уравнениях: числительные могут быть частью уравнений и неравенств, где они могут быть решением или неизвестным значением. Например, 3 + x = 8, где x = 5.

Эти основные свойства числительного позволяют использовать их для выполнения различных математических операций и решения задач.

Числительные в разных системах счисления

Наиболее распространенной системой счисления является десятичная система, которая использует десять цифр от 0 до 9. В десятичной системе числительные образуются с помощью этих цифр, например: 1, 2, 3, 10, 100 и т.д.

Однако в разных культурах и в разных системах счисления используются и другие числительные. Например, в двоичной системе счисления используются только две цифры — 0 и 1. Поэтому числительные в двоичной системе образуются с помощью этих двух цифр, например: 1, 10, 11, 100 и т.д.

Также существует восьмеричная и шестнадцатеричная системы счисления. В восьмеричной системе используются восемь цифр от 0 до 7, а в шестнадцатеричной системе — шестнадцать цифр от 0 до 9 и от A до F. Числительные в этих системах образуются аналогичным образом.

Интересно отметить, что в некоторых системах счисления, таких как римская система, числительные образуются с помощью букв. Например, в римской системе буква I обозначает 1, буква V — 5, буква X — 10 и т.д.

В зависимости от системы счисления, числительные могут иметь различные свойства и правила записи. Поэтому при работе с числительными в математике важно учитывать используемую систему счисления.

Вопрос-ответ:

Что такое числительное в математике?

Числительное в математике — это слово или выражение, которое обозначает количество предметов или объектов в группе или весьма точное значение числа.

Какие свойства имеют числительные в математике?

Свойства числительных в математике включают сложение, вычитание, умножение и деление. Они также могут быть положительными или отрицательными, целыми или десятичными.

Какие примеры числительных можно привести?

Примерами числительных могут быть: 3 (три), 7 (семь), 10 (десять), 0.5 (ноль целых пять десятых).

Можно ли использовать числительные в реальной жизни?

Да, числительные используются в реальной жизни для измерения количества предметов или объектов, например, при покупках в магазине, измерении расстояния или времени.

Какие еще математические операции можно использовать с числительными?

Кроме сложения, вычитания, умножения и деления, с числительными можно выполнять операции возведения в степень и извлечения корня. Также можно применять функции округления и преобразования в десятичную дробь.

Что такое числительное в математике?

Числительное в математике — это слово или выражение, которое обозначает количество или порядок предметов, явлений и т.д. Оно используется для измерения и учета количественных характеристик.

Какие свойства имеют числительные?

Числительные имеют несколько свойств. Во-первых, они могут быть классифицированы как кардинальные (обозначают количество предметов) и порядковые (обозначают порядок предметов в упорядоченной последовательности). Во-вторых, числительные могут быть простыми (состоят из одного слова) или сложными (состоят из нескольких слов или выражений). В-третьих, они могут быть положительными (обозначают положительные числа) и отрицательными (обозначают отрицательные числа).

Числительные в десятичной системе

Например, в числе 2457, цифра 2 находится на позиции сотен, цифра 4 на позиции десятков, цифра 5 на позиции единиц, а цифра 7 на позиции десятитысячных.

Числительные в десятичной системе можно разделить на две категории: натуральные числительные и десятичные дроби.

Натуральные числительные — это числа, которые используются для обозначения количества предметов. Они могут быть как положительными, так и нулем. Натуральные числительные включают все числа, начиная с 0 и увеличивающиеся на единицу.

Десятичные дроби — это числа, которые используются для обозначения части целого числа. Они состоят из целой части и десятичной части, разделенных десятичной запятой. Десятичные дроби могут быть как положительными, так и отрицательными.

Например, число 3,14 является десятичной дробью, где 3 — целая часть, а 14 — десятичная часть. Также число 0,5 является десятичной дробью, где 0 — целая часть, а 5 — десятичная часть.

Числительные в десятичной системе являются основой для многих математических операций, таких как сложение, вычитание, умножение и деление. Они позволяют нам работать с числами и решать различные задачи в математике и повседневной жизни.

Десятичные дроби в числительной форме

В десятичной дроби числитель представлен в виде конечного или бесконечного ряда цифр, разделенных запятой или точкой. Запятая или точка отделяет целую часть числа от десятичной части. Например, в числительной форме числа 3,14 целая часть равна 3, а десятичная часть равна 0,14.

Для записи бесконечных десятичных дробей, используют периодическую десятичную запись, где одна или несколько цифр повторяются бесконечно. Например, число 1/3 в числительной форме будет выглядеть как 0,3333333…

Десятичная дробьЧислительная форма

0,5	пять десятых
1,25	один целый и двадцать пять сотых
2,75	два целых и семьдесят пять сотых

Десятичные дроби в числительной форме позволяют удобно и точно описывать различные значения и результаты измерений. Они играют важную роль в научных расчетах, финансовой сфере и многих других областях жизни.

Числительные в римской системе счисления

Основные римские числительные:

• I — 1
• V — 5
• X — 10
• L — 50
• C — 100
• D — 500
• M — 1000

Числа в римской системе образуются путем суммирования и вычитания этих числительных. Правила записи и вычитания следующие:

• Если меньшая цифра стоит перед большей, их значения складываются. Например, II — 2, VI — 6.
• Если меньшая цифра стоит после большей, ее значение вычитается из значения большей цифры. Например, IV — 4, IX — 9.
• Цифра, повторенная несколько раз, обозначает сумму этих цифр. Например, III — 3, XX — 20.

Римские числительные используются до сих пор, например, для обозначения годов, номеров королевских правлений и т.д. Они также широко встречаются в исторических исследованиях, а также в литературе и искусстве.

Примеры использования числительных

В математике числительные широко используются для обозначения количества объектов или значений, а также для указания порядка или ранжирования элементов в последовательности. Рассмотрим несколько примеров использования числительных:

1. Количество элементов:

Числительные могут использоваться для обозначения количества элементов в наборе. Например, «в круге 7 точек» или «у меня 3 яблока».

2. Порядковые числительные:

Числительные могут также использоваться для указания порядка или ранжирования элементов в последовательности. Например, «первый», «второй», «третий» и т.д.

3. Интервалы и диапазоны:

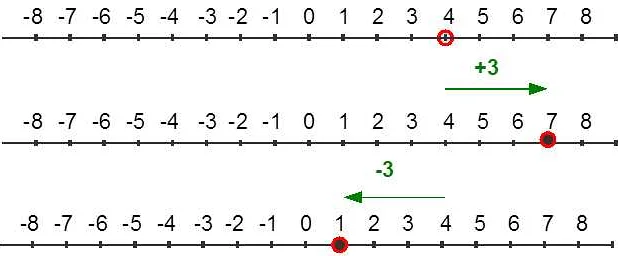
Числительные могут использоваться для обозначения интервалов и диапазонов значений. Например, «от 1 до 10», «с 5 по 15» или «в промежутке от -5 до 5».

4. Математические операции:

Числительные могут служить аргументами в математических операциях. Например, «сложить два числа», «умножить на пять», «разделить на три».

Приведенные примеры демонстрируют лишь некоторые способы использования числительных в математике. В зависимости от контекста, числительные могут иметь различные значения и использоваться в разных ситуациях.