Что такое порядок в математике

Порядок в математике — это концепция, которая определяет отношение между элементами множества. Он используется для установления относительного положения чисел, объектов или событий, а также для сравнения и упорядочивания данных. Порядок может быть линейным или частичным и имеет важное значение в различных областях математики, включая алгебру, теорию множеств и дискретную математику.

Порядок — одно из фундаментальных понятий в математике, которое определяет отношение между элементами множества. Оно позволяет устанавливать, какой элемент является первым, вторым, третьим и так далее. Понимание порядка в математике важно для решения многих задач и построения различных моделей.

Основные принципы порядка в математике основываются на транзитивности, антисимметричности и рефлексивности. Транзитивность означает, что если элемент A предшествует элементу B, и элемент B предшествует элементу C, то элемент A также предшествует элементу C. Антисимметричность означает, что если элемент A предшествует элементу B и элемент B предшествует элементу A, то A и B равны. Рефлексивность означает, что любой элемент предшествует самому себе.

Порядок можно представить в виде линейной упорядоченной структуры, называемой линейным порядком. В линейном порядке каждый элемент имеет определенное положение и предшествует или следует за другими элементами.

Порядок используется в различных областях математики, а также в других науках, таких как физика, химия, экономика и информатика. Он позволяет упорядочить данные и объекты, что ведет к более понятным и систематическим решениям задач.

Определение понятия «порядок» в математике

Порядок может быть определен на различных типах множеств: на числах, на множествах точек, на буквах и т. д. Он позволяет установить, какой элемент множества является меньшим или большим по сравнению с другим элементом.

В математике существуют разные типы порядков. Например, в числовом порядке элементы множества чисел упорядочиваются по их величине. В алфавитном порядке буквы располагаются в алфавитном порядке.

Порядок может быть задан с помощью отношений «меньше», «больше», «меньше или равно», «больше или равно» и т. д. Эти отношения устанавливаются на основе определенных правил и аксиом порядка.

Понимание и использование понятия «порядок» является важным для решения задач, связанных с сравнением элементов и упорядочиванием данных. Оно имеет широкое применение в различных областях математики, а также в других науках и повседневной жизни.

Порядок: что это такое?

Порядок может быть задан на различных множествах, например, на множестве натуральных чисел или на множестве точек на прямой. Определение порядка зависит от конкретного множества и может включать различные свойства и правила.

Важным свойством порядка является транзитивность. Это означает, что если элемент А расположен перед элементом В, а элемент В перед элементом С, то элемент А также будет расположен перед элементом С.

Другим важным свойством порядка является антисимметрия. Это означает, что если элемент А расположен перед элементом В, и элемент В расположен перед элементом А, то элементы А и В должны быть одинаковыми.

Порядок может быть задан с помощью различных символов и обозначений, таких как «», «≤» или «≥». Они указывают на направление порядка и позволяют сравнивать элементы множества.

Понимание порядка является важным для решения различных задач и проблем в математике. Он позволяет упорядочить данные и определить их взаимное положение, что является основой для дальнейшего анализа и выводов.

Таким образом, порядок в математике играет важную роль и позволяет установить отношение между элементами множества, определить их положение и сравнивать их между собой.

Основные принципы порядка

Основные принципы порядка в математике связаны с установлением отношения «больше», «меньше» или «равно» между числами. Они позволяют упорядочить числа в последовательности или на числовой прямой.

Первый принцип порядка — транзитивность. Если одно число больше другого, а второе число больше третьего, то первое число будет больше третьего. Например, если а > b и b > c, то а > c.

Второй принцип порядка — антисимметричность. Если одно число больше другого, то они не могут быть равны между собой. Например, если а > b, то а ≠ b.

Третий принцип порядка — линейность. Любые два числа можно сравнить между собой, то есть они либо будут равны, либо одно будет больше другого. Например, для любых чисел а и b, справедливо либо а > b, либо а = b, либо а < b.

Принципы порядка в математике помогают сортировать числа, упорядочивать их в последовательности или на числовой прямой, а также решать задачи, связанные с сравнением чисел.

Сравнение и упорядочение чисел

Для сравнения чисел используется знаки сравнения: «больше», «меньше» и «равно». Если число A больше числа B, то записывается A > B. Если число A меньше числа B, то записывается A < B. Если числа A и B равны, то записывается A = B.

Для упорядочения чисел применяется принцип сравнения. Если числа A и B сравниваются, то можно сравнить число A с другим числом C. Если A > C, то можно сделать вывод, что B > C. Аналогично, если A < C, то B < C. Таким образом, два числа сравниваются через третье число.

Для удобства и наглядности сравнения и упорядочения чисел, можно использовать таблицу сравнений. В таблице указываются числа и их отношения друг к другу. Например:

ЧислоОтношение

A	A > B, A > C
B	B < A, B < C
C	C < A, C < B

Такая таблица позволяет наглядно увидеть отношения между числами и определить их порядок.

Важно помнить, что порядок чисел зависит от выбранной системы сравнения. В некоторых системах сравнения могут применяться и другие знаки, например, «больше или равно» и «меньше или равно». Также стоит учитывать особенности сравнения дробных чисел и отрицательных чисел.

Порядок и операции

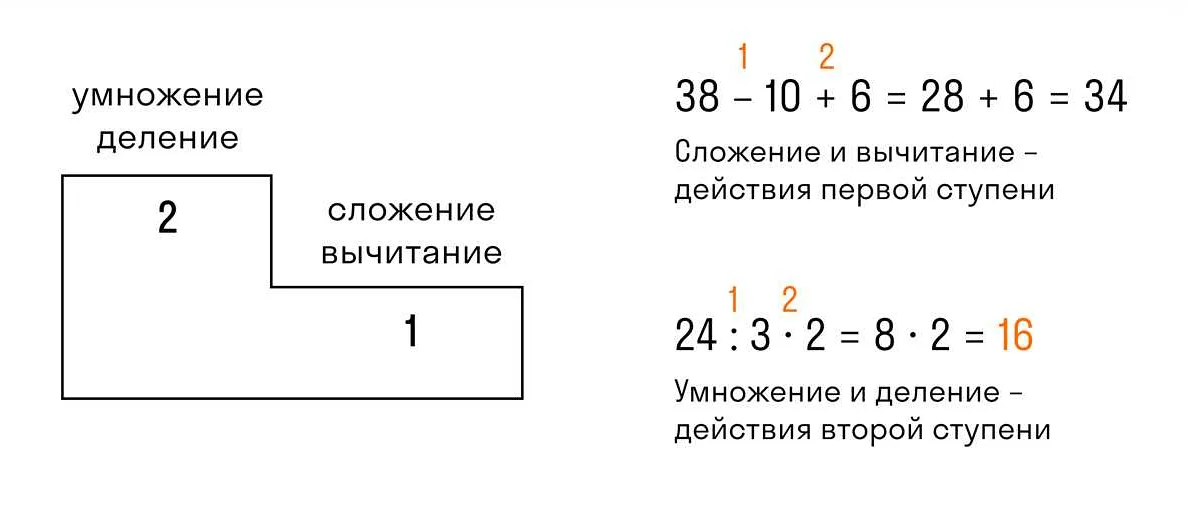
В математике порядок имеет особое значение при выполнении операций. Он определяет последовательность действий, которую нужно выполнить, чтобы получить правильный результат.

В общем случае, порядок операций определяется следующими правилами:

1. Сначала выполняются операции в скобках.
2. Затем выполняются умножение и деление.
3. В конце выполняются сложение и вычитание.

Важным принципом порядка является правило умножения и деления перед сложением и вычитанием. Это означает, что умножение и деление всегда выполняются перед сложением и вычитанием, даже если они находятся в другом порядке в выражении.

Например, в выражении 3 + 4 * 2 сначала выполняется умножение, а затем сложение. Результат будет равен 11: 4 * 2 = 8, 3 + 8 = 11.

Если нужно изменить порядок выполнения операций, можно использовать скобки. Скобки позволяют группировать операции и указывают, что операции внутри скобок должны быть выполнены первыми.

Например, в выражении (3 + 4) * 2 сначала выполняется операция в скобках, а затем умножение. Результат будет равен 14: 3 + 4 = 7, 7 * 2 = 14.

Правильный порядок выполнения операций важен для получения правильного результата. Поэтому в математике порядок играет значительную роль и должен быть учитыван при решении задач и вычислении значений.

Порядок и неравенства

В математике понятие порядка играет важную роль при сравнении чисел и выражений. Оно позволяет упорядочить элементы множества и определить их отношение друг к другу.

Основным инструментом для сравнения чисел являются неравенства. Неравенство — это выражение, в котором два числа или выражения сравниваются с помощью знаков «больше» (>), «меньше» (

Порядок чисел определяется следующими основными принципами:

1. Если два числа сравниваются с помощью знака «больше» (>) или «меньше» (
2. Если два числа сравниваются с помощью знака «больше или равно» (≥) или «меньше или равно» (≤), то число, стоящее слева от знака, является меньшим или равным, а число, стоящее справа от знака, — большим или равным.
3. При сравнении выражений с участием операций сложения и вычитания, сначала сравниваются их старшие члены. Если старшие члены равны, то сравниваются следующие по степени члены, и так далее.
4. При сравнении выражений с участием операций умножения и деления, сначала сравниваются их множители или делители. Если множители или делители равны, то сравниваются другие части выражений.
5. Порядок чисел может быть изменен при выполнении операций возведения в степень и извлечения корня. Например, извлечение корня из отрицательного числа приводит к комплексным числам, которые нельзя упорядочить по величине.

Знание порядка и умение работать с неравенствами позволяет решать различные задачи и доказывать математические утверждения.

Порядок и рациональные числа

Рациональные числа – это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Рациональные числа включают в себя все целые числа, а также все числа, которые можно представить в виде конечной или периодической десятичной дроби.

Порядок рациональных чисел определяется сравнением их десятичных представлений. Для сравнения двух рациональных чисел сначала сравниваются их целые части. Если они различны, то большее число – число с большей целой частью. Если целые части равны, то сравниваются дробные части чисел.

Сравнение десятичных дробей происходит путем сравнения цифр в соответствующих разрядах. Если цифры в разрядах равны, то сравниваются следующие разряды и так далее. Если все разряды чисел совпадают, то числа равны.

Пример:

Рациональное числоДесятичное представление

1/2	0.5
2/3	0.6666…
3/4	0.75

Исходя из десятичных представлений, можно сравнить эти рациональные числа и установить порядок между ними:

Рациональные числаПорядок

1/2	Меньше
2/3	Меньше
3/4	Больше

Таким образом, в математике порядок помогает упорядочить рациональные числа и определить их взаимное положение на числовой прямой или в таблице сравнения чисел.

Порядок и иррациональные числа

В математике существует два основных типа чисел: рациональные и иррациональные. Рациональные числа можно представить в виде обыкновенных дробей, где числитель и знаменатель являются целыми числами. Иррациональные числа, в свою очередь, не могут быть представлены в виде обыкновенной дроби и имеют бесконечную десятичную дробь без повторяющихся цифр.

При сравнении рациональных чисел, порядок определяется сравнением числителей и знаменателей. Например, если у нас есть две рациональные числа: 1/2 и 3/4, то мы можем сказать, что 1/2 меньше 3/4.

Однако, при сравнении иррациональных чисел, порядок становится более сложным. В этом случае мы не можем использовать простое сравнение чисел, как в случае с рациональными числами. Например, если у нас есть два иррациональных числа: √2 и √3, то невозможно сказать, какое из них больше или меньше.

Вместо этого, для сравнения иррациональных чисел мы используем другие методы и приближенные значения. Мы можем приближенно вычислить значения иррациональных чисел и сравнить их таким образом. Например, мы можем вычислить приближенные значения √2 и √3 и сравнить их с помощью десятичной дроби.

Таким образом, порядок в математике применяется не только к рациональным числам, но и к иррациональным числам. Он позволяет упорядочивать числа и сравнивать их между собой, что является важным принципом для работы с числами и решения математических задач.

Видео по теме:

Что такое порядок в математике?

В математике порядок отношений определяет, как элементы множества расположены друг относительно друга. Он позволяет сравнивать элементы на «больше» или «меньше».

Какие основные принципы лежат в основе порядка в математике?

Основными принципами порядка являются рефлексивность (любой элемент множества всегда больше или равен самому себе), антисимметричность (если один элемент больше другого, то другой элемент не может быть больше первого) и транзитивность (если один элемент больше второго, а второй элемент больше третьего, то первый элемент также больше третьего).

Как можно представить порядок в математике?

Порядок можно представить с помощью отношения «больше» или «меньше», либо с помощью символов «>» и »

Зачем нужен порядок в математике?

Порядок в математике играет важную роль при сравнении элементов и установлении отношений между ними. Он позволяет упорядочить данные и сделать выводы о их взаимосвязи. Например, порядок чисел на числовой оси позволяет определить, какое число больше или меньше другого.

В каких областях математики применяется понятие порядка?

Понятие порядка применяется во многих областях математики, таких как алгебра, теория чисел, математическая логика, топология и дискретная математика. Оно также находит применение в других науках, например, в физике, экономике и компьютерных науках.

Что такое порядок в математике?

Порядок в математике — это упорядочивание элементов в некотором множестве. Он определяет отношение между элементами множества и позволяет сравнивать их величину, определять наименьший и наибольший элементы, а также строить упорядоченные ряды или последовательности.