Что такое числовой луч в математике 3 класс

Числовой луч в математике 3 класс – это предмет изучения, который помогает детям понять и представить числа на числовой прямой. Учебная статья подробно объясняет, как использовать числовой луч для определения положительных и отрицательных чисел, а также показывает его применение в задачах и играх.

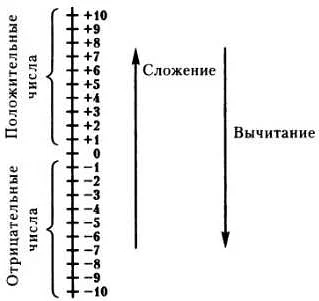
Числовой луч – это важное понятие в математике, которое изучается уже в третьем классе. Он помогает детям лучше понять и визуализировать числа на числовой прямой. Числовой луч представляет собой отрезок со стрелкой, который начинается с нуля и продолжается вправо бесконечно. Он помогает представить положительные числа и их порядок на числовой прямой.

Использование числового луча помогает третьеклассникам лучше понять различные математические понятия, такие как сравнение чисел, сложение и вычитание, а также умножение и деление. Они могут легко определить, какое число больше или меньше, насколько они отличаются друг от друга. Числовой луч также помогает детям представлять числа разными способами, например, в виде десятков и единиц, и легко переходить от одного представления к другому.

Использование числового луча может быть интерактивным и веселым. Дети могут играть в игры, в которых им нужно перемещаться по числовому лучу, отмечая числа и решая задачи. Это помогает им лучше усваивать материал и развивать навыки в работе с числами. Числовой луч – это не только учебный инструмент, но и игровой элемент, который делает изучение математики увлекательным и интересным для детей.

Определение числового луча в математике

Например, если мы имеем числовой луч, начинающийся с точки 2, то все числа, которые больше 2 и находятся справа от него, будут принадлежать этому числовому лучу. Он будет обозначаться как (2, +∞) или как «>2».

Числовые лучи могут быть как положительными, так и отрицательными. Например, если числовой луч начинается с точки -3 и продолжается до -∞, он будет обозначаться как (-∞, -3) или как «

Числовые лучи часто используются в математике для задания интервалов и решения уравнений. Они позволяют удобно представлять множества чисел на числовой прямой и определять их взаимное расположение.

Видео по теме:

Как изображать числовой луч на плоскости

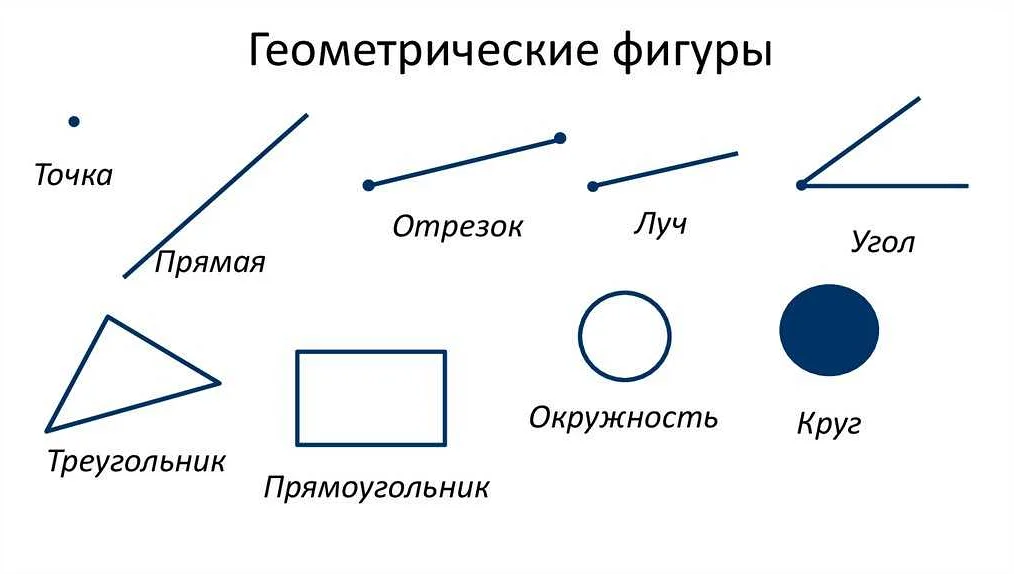
Для изображения числового луча на плоскости нужно использовать прямую линию, которая начинается с определенной точки и продолжается в одном направлении бесконечно.

Чтобы задать числовой луч, нужно выбрать начальную точку и указать направление, в котором луч будет располагаться. Начальная точка обычно обозначается точкой на числовой оси, а направление указывается стрелкой, которая указывает на положительные числа.

Числовой луч можно изобразить на плоскости горизонтальной прямой. Начальная точка будет находиться на этой прямой, а направление будет указывать вправо от этой точки.

Также можно изображать числовой луч на плоскости вертикальной прямой. В этом случае начальная точка будет находиться на этой прямой, а направление будет указывать вверх от этой точки.

Изображение числового луча на плоскости позволяет наглядно представить его направление и позволяет легко сравнивать числа, находящиеся на разных частях луча.

Понятие начала и конца числового луча

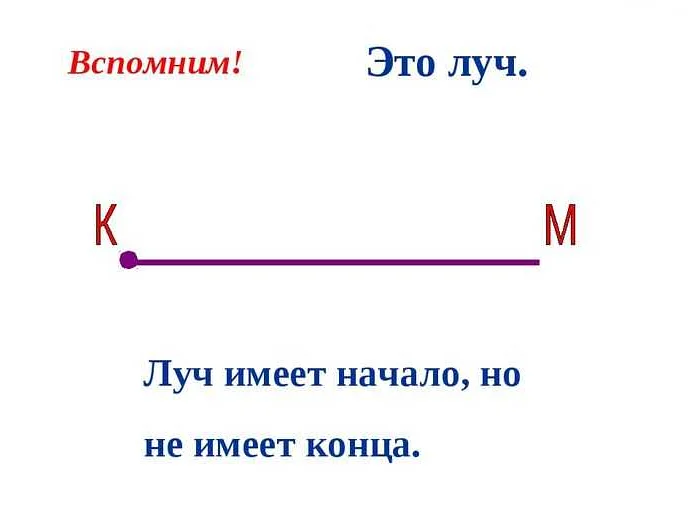
Начало числового луча обозначается точкой на числовой прямой, которая является начальной точкой луча. Конец числового луча также обозначается точкой на числовой прямой, которая является конечной точкой луча. Начало и конец числового луча важны для определения направления, в котором находятся числа на прямой.

Обозначение начала и конца числового луча может быть различным. В некоторых случаях используются буквы, например, «A» и «B». В других случаях, начало и конец числового луча могут быть обозначены числами, например, «0» и «1». Важно помнить, что обозначение начала и конца числового луча не влияет на его свойства и функциональность.

Зная начало и конец числового луча, можно определить, какие числа находятся на этом луче. Например, если начало числового луча обозначено числом 0, а конец обозначено числом 10, то все числа от 0 до 10 включительно находятся на этом луче.

Понимание понятия начала и конца числового луча является важным для работы с числовыми лучами и их использования в математических задачах и вычислениях.

Вопрос-ответ:

Что такое числовой луч в математике?

Числовой луч в математике — это отрезок на числовой прямой, который имеет начало в определенном числе и стремится до бесконечности в одном направлении.

Как использовать числовой луч в математике?

Числовой луч может использоваться для представления и сравнения чисел. Например, мы можем использовать числовой луч, чтобы сравнить два числа и определить, какое из них больше или меньше.

Как найти среднее значение на числовом луче?

Чтобы найти среднее значение на числовом луче, нужно найти сумму всех чисел на луче и разделить ее на количество чисел.

Какие операции можно выполнять на числовом луче?

На числовом луче можно выполнять операции сложения и вычитания. Например, если на луче есть число 5, мы можем сложить с ним другое число, чтобы получить сумму, или вычесть из него число, чтобы получить разность.

Можно ли использовать числовой луч для решения уравнений?

Да, числовой луч можно использовать для решения уравнений. Например, если у нас есть уравнение x + 3 = 8, мы можем представить все возможные значения x на числовом луче и найти значение, которое удовлетворяет уравнению.

Как читать числовой луч

Чтение числового луча осуществляется слева направо или справа налево, в зависимости от порядка чисел на луче. Для чтения чисел на числовом луче используются следующие правила:

1. Слева направо: начиная с точки начала, читаем числа по порядку, двигаясь вправо по числовому лучу.
2. Справа налево: начиная с бесконечной стрелки, читаем числа по порядку, двигаясь влево по числовому лучу.

При чтении числового луча важно обратить внимание на знаки чисел и их величину. Положительные числа располагаются справа от нуля, а отрицательные — слева от нуля. Числа на числовом луче также могут быть отмечены точками или другими символами для более наглядного представления.

Чтение числового луча помогает детям понять порядок чисел и их взаимосвязь на числовой прямой. Это важная навык для развития математического мышления и решения задач, связанных с числами и их величиной.

Примеры использования числового луча в математике

Пример 1:

Представьте, что у вас есть числовой луч, и на нём отмечены числа от 1 до 10. Вы хотите найти сумму всех чисел от 1 до 5. С помощью числового луча вы можете визуализировать эту сумму. Начиная с числа 1, вы можете двигаться вправо и считать числа до 5, а затем прибавить их.

1 + 2 + 3 + 4 + 5 = 15

Пример 2:

Представьте, что у вас есть числовой луч, и на нём отмечены числа от -5 до 5. Вы хотите найти произведение всех чисел от -3 до 3. С помощью числового луча вы можете визуализировать это произведение. Начиная с числа -3, вы можете двигаться вправо и перемножать числа до 3, а затем умножить полученное произведение на -1 (так как есть отрицательные числа).

(-3) * (-2) * (-1) * 1 * 2 * 3 = 36

Пример 3:

Представьте, что у вас есть числовой луч, и на нём отмечены числа от 0 до 100. Вы хотите найти среднее арифметическое всех чисел от 10 до 30. С помощью числового луча вы можете визуализировать это среднее арифметическое. Начиная с числа 10, вы можете двигаться вправо и считать числа до 30, а затем найти их сумму и разделить на количество чисел, чтобы получить среднее арифметическое.

(10 + 11 + 12 + … + 30) / 21 = 20

Различные типы числовых лучей

В математике существует несколько различных типов числовых лучей, которые могут быть использованы для представления числовых диапазонов и отношений между числами.

Обычный числовой луч: это самый простой и распространенный тип числового луча. Он представляет положительные и отрицательные числа на числовой оси. Ноль обычно располагается в центре, а положительные числа находятся справа от нуля, а отрицательные числа — слева.

Направленный числовой луч: в отличие от обычного числового луча, у которого ноль находится в центре, направленный числовой луч имеет начало в любой точке на числовой оси и распространяется только в одном направлении. Направление обычно указывается стрелкой на конце луча.

Круговой числовой луч: это числовой луч, который представляет числа на окружности. Числа располагаются в порядке возрастания или убывания вдоль окружности. Круговой числовой луч может быть полным, представляющим все числа, или может быть частичным, ограниченным определенным углом.

Расширенный числовой луч: это числовой луч, который включает бесконечные значения в обоих направлениях. Он представляет все рациональные и иррациональные числа, а также бесконечность.

Использование различных типов числовых лучей может помочь визуализировать и понять числовые диапазоны и отношения между числами.

Сравнение числовых лучей

Сравнение числовых лучей в математике очень важно для понимания отношений между числами. Числовой луч представляет собой прямую линию, на которой размещены числа и знаки сравнения. Сравнивая два числовых луча, мы можем определить, какое число больше или меньше.

Для сравнения числовых лучей используются знаки сравнения: больше ( > ), меньше ( < ) и равно ( = ). Знаки сравнения указывают направление движения по числовому лучу при сравнении двух чисел.

Например, если мы хотим сравнить числа 5 и 8, мы можем нарисовать два числовых луча и поставить числа на них. Затем мы рассмотрим, в какую сторону нужно двигаться по лучу, чтобы дойти от 5 до 8. При сравнении числовых лучей мы можем использовать знаки сравнения: 5 < 8 или 5 меньше 8, так как мы двигаемся вправо по лучу от числа 5 к числу 8.

Таким образом, сравнение числовых лучей помогает нам определить, какое число больше или меньше, и устанавливает отношения между числами.

Применение числовых лучей в повседневной жизни

Одним из применений числовых лучей является ориентация во времени. Например, можно использовать числовые лучи для отображения расписания занятий или плана на день. Это поможет детям и взрослым лучше ориентироваться во времени и планировать свои активности.

Ещё одним примером использования числовых лучей может быть отслеживание финансовых расходов. Можно создать числовой луч, где каждая отметка представляет определенную сумму денег, и отмечать на нем свои ежедневные траты. Таким образом, вы сможете легко контролировать свои расходы и видеть, на что уходят ваши деньги.

Числовые лучи также могут быть полезны для сравнения и классификации разных объектов. Например, можно создать числовой луч, где каждая отметка представляет определенный размер или вес, и сравнивать на нем разные предметы. Это поможет лучше понять отношение между объектами и сделать правильный выбор.

Таким образом, использование числовых лучей в повседневной жизни может помочь в ориентации во времени, контроле финансовых расходов, сравнении и классификации объектов. Они являются удобным и наглядным инструментом, который помогает лучше понять числовые отношения и сделать правильные решения.