Что такое прямой луч в математике

Прямой луч в математике — это часть прямой линии, которая начинается в определенной точке и продолжается бесконечно в одном направлении. Узнайте, как определить и использовать прямой луч в геометрии и алгебре.

В математике прямой луч является одной из основных геометрических фигур. Он представляет собой бесконечный отрезок, который начинается в одной точке и распространяется в бесконечность в одном направлении. Прямой луч обладает рядом свойств, которые делают его полезным инструментом в различных математических задачах.

Одно из основных свойств прямого луча — это то, что он имеет только одно начало, но не имеет конца. Это означает, что точка начала прямого луча является его единственной точкой, а все остальные точки лежат на самом луче и расположены вдоль его направления. Прямой луч также является пространственной фигурой, которая простирается только в одном измерении — по прямой линии.

Прямой луч может иметь различные направления, которые определяются положительной или отрицательной ориентацией. Если направление прямого луча указывается вправо от его начала, то он называется положительным. Если направление указывается влево, то луч считается отрицательным.

Прямые лучи широко используются в разных областях математики, физики и геометрии. Они помогают в решении задач связанных с направлением движения, временем, пространством и многими другими концепциями. Прямой луч — это мощный инструмент, который помогает нам понять и описать мир вокруг нас и его математические законы.

Что такое прямой луч в математике?

Прямой луч обладает рядом важных свойств:

• Прямой луч имеет только одно начальное положение и направление.
• Прямой луч не имеет конца и продолжается бесконечно в одном направлении.
• Любые две точки на прямом луче можно соединить отрезком, который будет лежать полностью на прямой луче.
• Прямой луч может пересекать другие прямые и плоскости.
• Прямой луч может быть направлен вверх, вниз, вправо или влево в зависимости от контекста.

Прямой луч часто используется в геометрии для определения направления, расстояния и осей координатной плоскости. Примерами прямых лучей являются лучи света, линии движения тела и многие другие.

Видео по теме:

Определение прямого луча

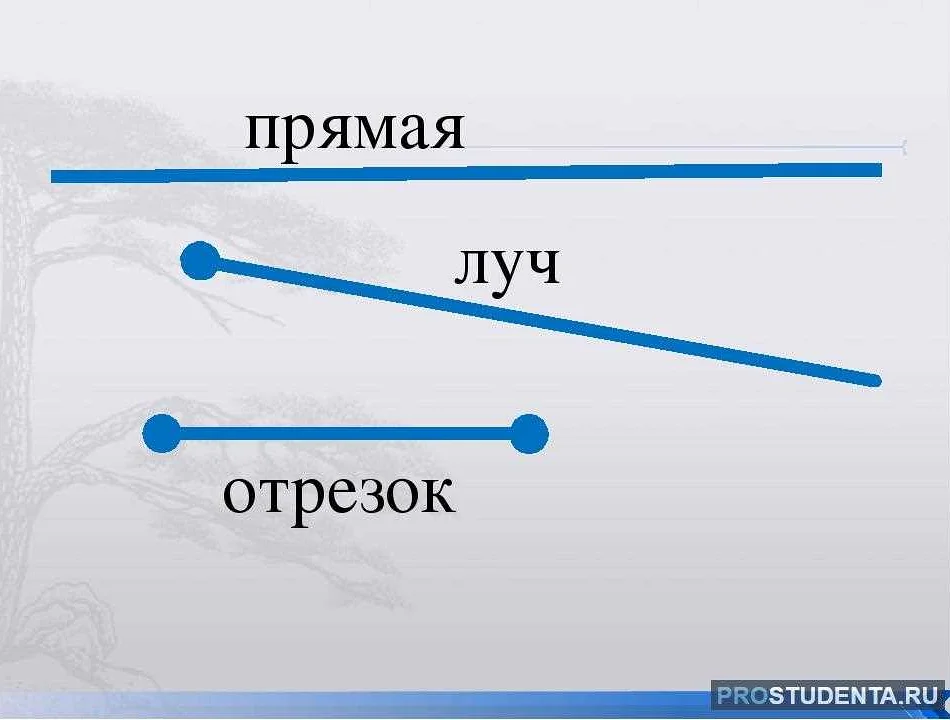
Прямой луч обозначается с помощью символа → над двумя точками, где начальная точка находится слева, а стрелка указывает направление продолжения луча.

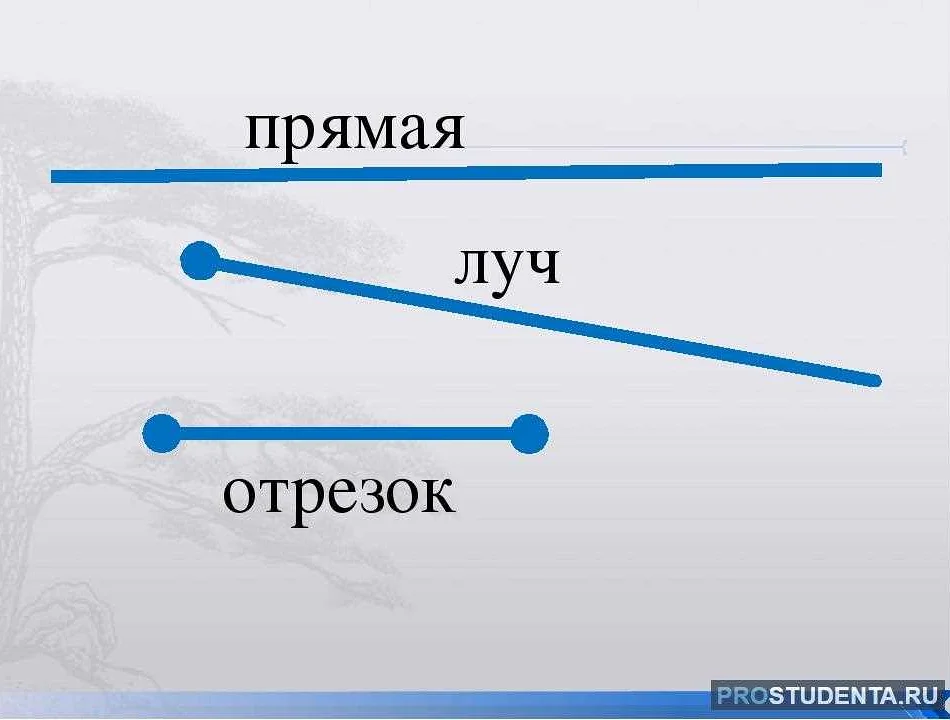
Прямой луч можно представить графически как отрезок прямой, который начинается в определенной точке и стремится к бесконечности в одном направлении.

Прямой луч очень похож на полуоткрытый луч, но в отличие от полуоткрытого луча, прямой луч не имеет конечной точки.

Прямой луч играет важную роль в математике, особенно в геометрии, и используется для определения и изучения различных понятий, таких как углы, отрезки, плоскости и т.д.

Свойства прямого луча

Прямой луч имеет несколько свойств:

1. Начало и направление: прямой луч определен начальной точкой и направлением, которое указывает на бесконечность.

2. Не имеет конца: прямой луч продолжается в одном направлении бесконечно далеко.

3. Определенная длина: хотя прямой луч продолжается в бесконечность, мы можем измерить его часть с определенной длиной.

4. Не имеет ширины: прямой луч является одномерным объектом и не имеет ширины.

5. Не имеет изгибов: прямой луч всегда прямой и не может изгибаться.

6. Проходит через начальную точку: прямой луч всегда проходит через свою начальную точку и не может отклоняться от нее.

7. Не имеет середины: прямой луч не имеет точки, которая была бы его серединой, так как он продолжается в одном направлении.

8. Как любой луч, прямой луч может быть расширен в обратном направлении, образуя прямую линию.

Вопрос-ответ:

Что такое прямой луч?

Прямой луч – это часть прямой, которая начинается в определенной точке и продолжается бесконечно в одном направлении.

Как можно определить прямой луч?

Прямой луч можно определить с помощью двух параметров: начальной точки, из которой он исходит, и направления, в котором он распространяется.

Какие свойства имеет прямой луч?

Прямой луч не имеет конца, он продолжается бесконечно в одном направлении. Он также не имеет ширины и не может пересечь сам себя.

Как можно использовать прямой луч в математике?

Прямой луч используется для задания направления или ориентации в пространстве. Он также может быть использован для построения геометрических фигур и решения задач в различных областях математики.

Можете привести примеры использования прямого луча?

Примеры использования прямого луча в математике включают построение углов, определение направления движения объектов, задание границы для радиуса сходимости степенного ряда и многое другое.

Что такое прямой луч?

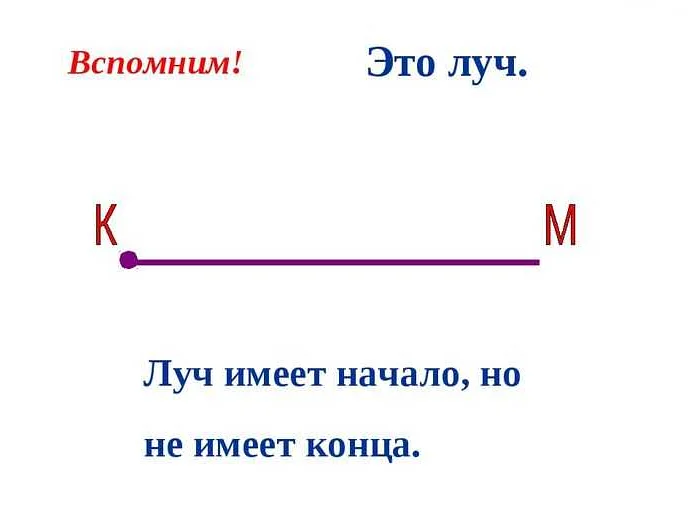
Прямой луч — это часть прямой линии, которая начинается в определенной точке, называемой началом луча, и продолжается в одном направлении бесконечно далеко.

Какие свойства прямого луча?

Прямой луч имеет два основных свойства. Во-первых, он имеет начальную точку, которая определяет его положение. Во-вторых, прямой луч продолжается бесконечно далеко в одном направлении.

Примеры использования прямого луча

Прямой луч используется в различных контекстах и приложениях в математике. Ниже приведены несколько примеров использования прямого луча:

1. Геометрия: в геометрии прямой луч используется для определения направления и бесконечности. Например, в определении угла прямой луч используется для указания начала и направления двух линий.
2. Физика: в физике прямой луч используется для моделирования падения света или других электромагнитных волн. Прямой луч служит для определения направления распространения энергии.
3. Оптика: в оптике прямой луч используется для описания траектории света при его распространении через прозрачные среды или при отражении и преломлении.
4. Геодезия: в геодезии прямой луч используется для измерения расстояний и углов при проведении геодезических работ. Прямой луч служит для определения точек и направления в пространстве.
5. Математическое моделирование: в математическом моделировании прямой луч используется для построения функциональных зависимостей и аппроксимации данных. Прямой луч помогает представить и определить значения в заданной области.

Прямой луч является важным инструментом для визуализации, анализа и решения различных задач в математике и ее приложениях. Его свойства и использование широко применяются в разных научных и практических областях.

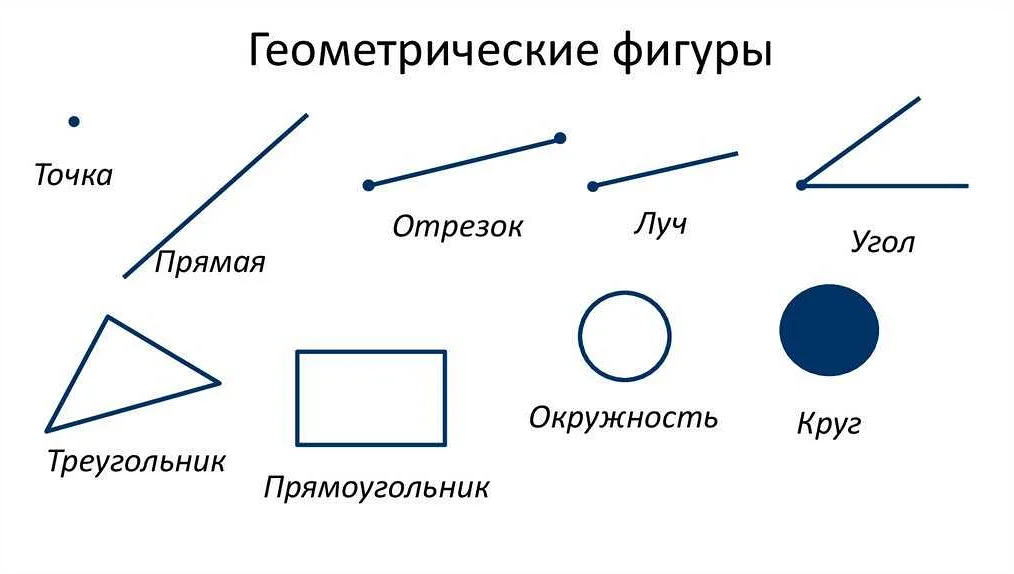
Прямой луч и геометрические фигуры

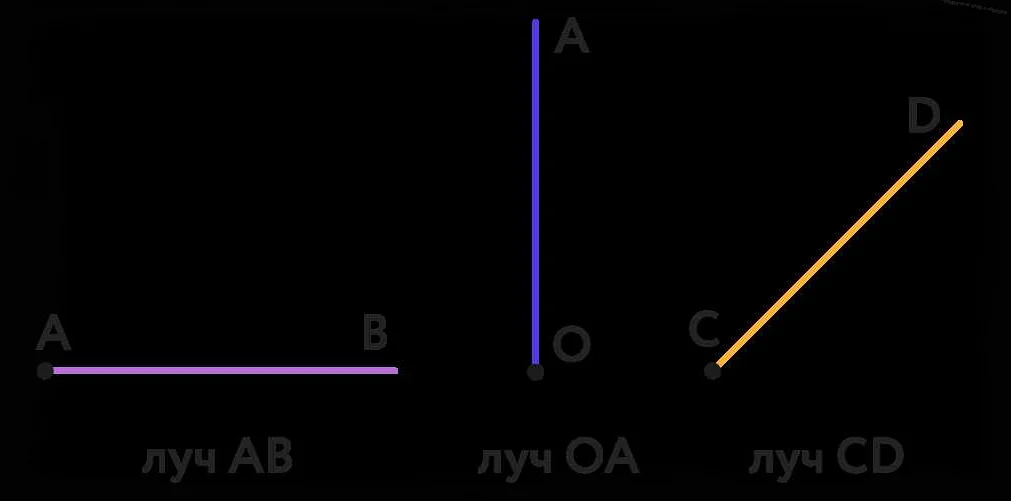
Прямой луч используется в геометрии для определения и изучения различных геометрических фигур. Он может быть использован для построения отрезков, углов, треугольников и других фигур.

Например, при построении треугольника с помощью прямого луча, мы можем использовать его для задания сторон треугольника. Для этого мы проводим прямой луч от одного из вершин треугольника и продолжаем его до пересечения с другой стороной. Таким образом, мы можем определить одну из сторон треугольника с помощью прямого луча.

Также прямой луч может быть использован для определения углов. Например, если мы проведем прямой луч от вершины угла, мы можем использовать его для измерения угла или для построения других углов, используя его в качестве базовой линии.

Таким образом, прямой луч играет важную роль в геометрии и позволяет нам изучать и определять различные геометрические фигуры.

Прямый луч и углы

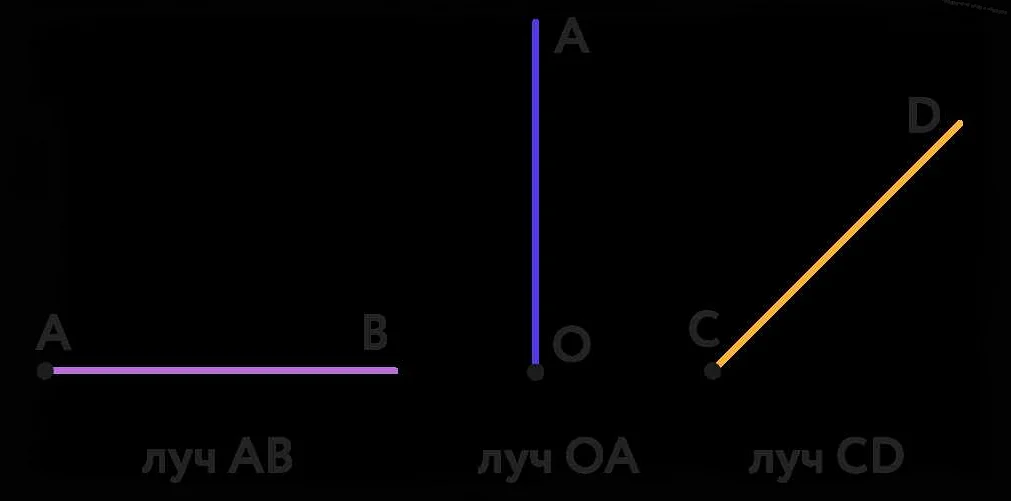
Прямые лучи могут быть использованы для определения и измерения углов. Угол — это фигура, образованная двумя лучами, которые имеют общую начальную точку. Начальная точка угла называется вершиной, а лучи — сторонами угла.

Углы могут быть классифицированы в зависимости от их величины.

• Острые углы: углы, меньшие 90 градусов.
• Прямые углы: углы, равные 90 градусам.
• Тупые углы: углы, больше 90 градусов и меньше 180 градусов.
• Полные углы: углы, равные 180 градусам.
• Рефлексивные углы: углы, больше 180 градусов и меньше 360 градусов.

Прямые лучи и углы используются в различных областях математики, физики и геометрии для решения задач и анализа пространственных отношений.

Прямой луч и прямые

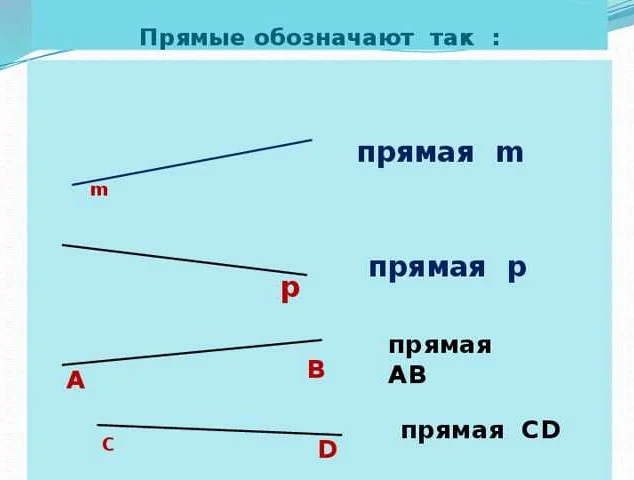
Прямой луч ABПрямой луч BC

Прямые — это линии, которые не имеют начала или конца. Они простираются в обе стороны бесконечно и не имеют изгибов. Прямая может быть представлена в виде бесконечной прямой линии:

Прямая AB

Прямая луч и прямая могут быть определены с помощью математических уравнений. Например, прямой луч AB может быть определен уравнением x ≥ 0, где x — координата точки на прямой линии. Прямая AB может быть определена уравнением x ∈ R, где R — множество всех действительных чисел.

Прямые играют важную роль в математике и геометрии. Они используются для описания и анализа форм, движения и взаимодействия объектов. Прямые также являются основой для других геометрических фигур, таких как треугольники, окружности и многоугольники.