Что такое луч в математике кратко
Содержимое
- 1 Что такое луч в математике кратко
- 1.1 Луч в математике: основные понятия и определения
- 1.2 Простое объяснение луча
- 1.3 Границы луча и их обозначения
- 1.4 Примеры лучей в жизни и математике
- 1.5 Свойства луча в математике
- 1.6 Бесконечность луча
- 1.7 Направление луча
- 1.8 Пересечение лучей
- 1.9 Применение лучей в различных областях
- 1.10 Геометрические конструкции с использованием лучей
- 1.11 Вопрос-ответ:
- 1.11.0.1 Зачем нужны лучи в математике?
- 1.11.0.2 Как можно представить луч графически?
- 1.11.0.3 Какие бывают типы лучей?
- 1.11.0.4 Можно ли нарисовать луч, который начинается с отрицательной точки?
- 1.11.0.5 Какие свойства имеют лучи?
- 1.11.0.6 Что такое луч в математике?
- 1.11.0.7 Как можно представить луч в математике?
- 1.12 Видео по теме:
Луч в математике — это часть прямой, которая начинается в определенной точке и не имеет конца. Узнайте, как определить луч и как он используется в различных математических задачах.
В математике луч — это геометрическая конструкция, которая состоит из точки, называемой началом луча, и всех точек на прямой, которые находятся в одной и той же стороне от начала. Луч имеет бесконечную протяженность в одном направлении и ограничен в противоположном направлении.
Лучи в математике используются для указания направления, измерения углов и задания границы для различных геометрических фигур и объектов. Они являются важным инструментом в геометрии и алгебре.
Луч можно представить себе как бесконечно длинную стрелку, у которой есть только начало и направление, но нет конца.
Лучи могут быть прямыми или кривыми, вертикальными или горизонтальными, параллельными или пересекающимися. Они также могут быть использованы для определения отрезков, углов и других геометрических объектов.
Понимание лучей в математике помогает решать задачи геометрии, алгебры и других разделов математики. Они помогают нам визуализировать и понять мир геометрических форм и отношений, что имеет важное значение в повседневной жизни и во многих профессиональных областях.
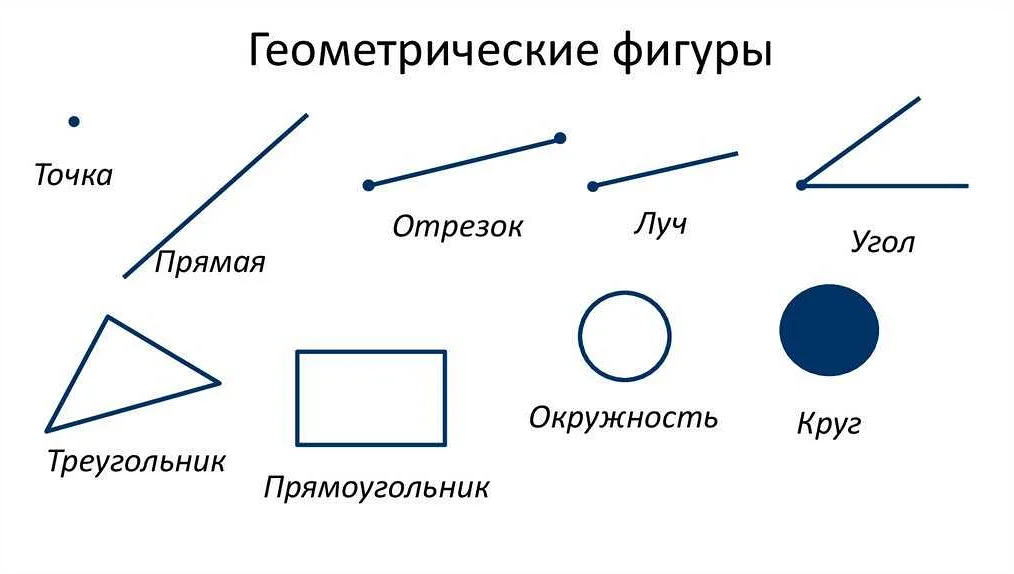
Луч в математике: основные понятия и определения
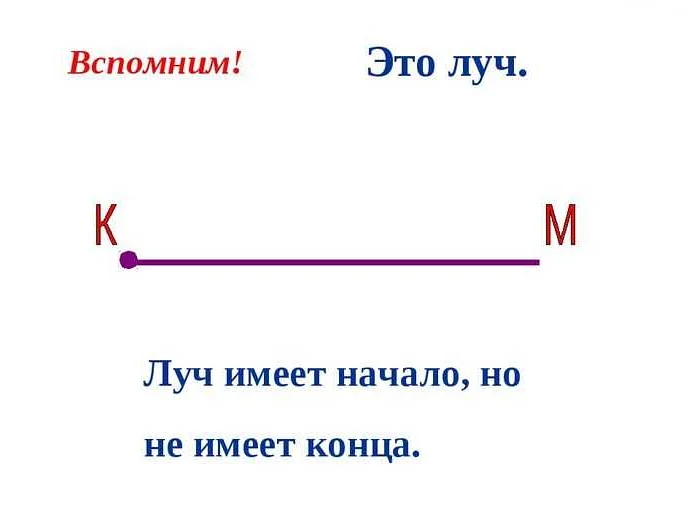
Начальная точка луча называется его началом. Она определяет, с какой точки начинается луч. Направление луча определяется тем, в какую сторону он продолжается. Луч может быть направлен влево или вправо, вверх или вниз.
Луч в математике обозначается маленькой буквой с надстрочной стрелкой над ней. Например, луч, начинающийся в точке A и направленный вправо, обозначается как AB. Луч, начинающийся в точке C и направленный вверх, обозначается как CD.
Основное свойство луча — его бесконечность. Луч продолжается бесконечно в одном направлении и не имеет конечной точки. Это значит, что если двигаться вдоль луча, то можно продолжать движение сколько угодно долго без остановки.
Лучи используются в математике для решения различных задач и построения геометрических фигур. Они помогают определить направление, расстояние и взаимное расположение точек и объектов в пространстве.
Простое объяснение луча
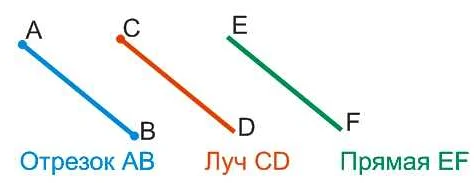
Луч обычно обозначается двумя точками: начальной точкой (началом луча) и другой произвольной точкой на луче, которая может быть отмечена стрелкой.
Луч может быть направлен влево или вправо. Луч, направленный влево, обычно обозначается символом «» перед начальной точкой.
Примеры использования луча:
| Луч AB |  |
| Луч CD |  |
| Луч EF |  |
Лучи могут использоваться для определения направления, расстояния и отношений между точками и объектами в математике и геометрии. Они также широко используются в физике и других науках.
Границы луча и их обозначения

Если луч направлен вправо, то его границу можно обозначить буквой «плюс» (+) или символом бесконечности (∞). Это означает, что луч продолжается бесконечно вправо.
Если луч направлен влево, то его границу можно обозначить буквой «минус» (-) или символом минус бесконечности (-∞). Это означает, что луч продолжается бесконечно влево.
Иногда границы луча обозначаются числами. Например, луч с начальной точкой в точке A и границей в точке B обозначается как [A, B). Здесь квадратная скобка указывает, что точка A является начальной точкой луча, а круглая скобка указывает, что точка B не включается в луч.
Важно помнить, что границы луча могут быть как открытыми, так и закрытыми. Открытая граница означает, что точка границы не входит в луч, а закрытая граница означает, что точка границы входит в луч.
Например, луч с начальной точкой в точке C и границей в точке D может быть обозначен как (C, D]. Здесь круглая скобка указывает, что точка C не включается в луч, а квадратная скобка указывает, что точка D является границей луча и входит в него.
Знание обозначений и границ луча поможет вам точно указывать интервалы на числовой оси и в работе с математическими моделями.
Примеры лучей в жизни и математике
В математике лучами называются отрезки, которые имеют начальную точку (начало луча) и продолжаются бесконечно в одном направлении.
Примеры лучей в жизни и математике:
- Солнечный луч: это световой луч, идущий от Солнца до Земли или любого другого объекта, освещая его и создавая тени.
- Луч света: в оптике, луч света представляет собой путь, по которому свет распространяется от источника света.
- Луч надежды: это символический луч, который олицетворяет надежду и оптимизм в трудных ситуациях.
- Геометрический луч: в геометрии, луч — это прямая линия, которая имеет начальную точку и простирается в бесконечность.
Лучи играют важную роль в математике и нашей повседневной жизни. Они помогают нам понять направление и распространение света, символизируют надежду и оптимизм, а также используются для описания геометрических форм и объектов.
Свойства луча в математике
У луча есть несколько важных свойств:
1. Направление: Луч имеет определенное направление, которое задается стрелкой, указывающей на бесконечность.
2. Начало: Луч начинается в определенной точке, которая является его началом.
3. Бесконечность: Луч продолжается бесконечно далеко в одном направлении.
4. Именование: Луч может быть обозначен одной буквой в верхнем регистре, например, луч А.
5. Длина: Луч не имеет конкретной длины, так как продолжается до бесконечности.
Примеры:
Луч А начинается в точке A и продолжается до бесконечности в определенном направлении.
Луч B начинается в точке B и также продолжается до бесконечности в другом направлении.
Бесконечность луча
Бесконечность луча означает, что луч не имеет конечной длины и не имеет окончания. Он продолжается бесконечно в одном направлении, не имея какой-либо точки остановки.
Луч может быть направлен вправо или влево от заданной начальной точки. Луч, направленный вправо, называется положительным лучом, а луч, направленный влево, называется отрицательным лучом.
Бесконечность луча в математике является удобным инструментом для описания направления и бесконечности прямых линий. С помощью лучей можно определить отрезки, углы и другие геометрические фигуры.
Направление луча
В математике понятие «луч» используется для обозначения бесконечно продолжающейся прямой линии, которая начинается в определенной точке и продолжается в одном направлении. Направление луча можно определить с помощью двух основных понятий: направление вправо и направление влево.
Направление луча вправо обозначается стрелкой, которая указывает на бесконечно продолжающуюся линию вправо от начальной точки. Луч вправо можно представить как бесконечно продолжающуюся положительную полуось координатной плоскости.
Направление луча влево обозначается стрелкой, которая указывает на бесконечно продолжающуюся линию влево от начальной точки. Луч влево можно представить как бесконечно продолжающуюся отрицательную полуось координатной плоскости.
Направление луча играет важную роль в геометрии и анализе. Оно позволяет определить положение и направление объектов на координатной плоскости и описать их движение. Понимание направления луча помогает в решении задач и построении графиков функций.
Пересечение лучей
Лучи в математике представляют собой бесконечные отрезки, имеющие начальную точку и направление. Возникает вопрос, что происходит, когда два луча пересекаются.
Пересечение лучей может иметь несколько вариантов:
- Если два луча пересекаются в одной точке, то говорят, что они пересекаются точечно. В этом случае, пересечение лучей будет просто являться этой точкой.
- Если два луча пересекаются на протяжении некоторого отрезка, то говорят, что они пересекаются отрезком. В этом случае, пересечение лучей будет представлять собой отрезок, который образуется в результате пересечения двух лучей.
- Если два луча не пересекаются, то говорят, что они не имеют общих точек. В этом случае, пересечение лучей будет пустым множеством.
Пересечение лучей имеет важное значение в геометрии и математике в целом. Оно используется для решения различных задач, например, для определения точки пересечения двух прямых или для поиска общих точек между лучами и другими геометрическими объектами.
Применение лучей в различных областях
- Геометрия: Лучи используются для определения и изучения геометрических фигур. Они помогают определить направление и расположение объектов в пространстве. Например, лучи могут использоваться для построения углов, треугольников и окружностей.
- Оптика: Лучи света используются для изучения свойств и взаимодействия света с различными поверхностями. Оптика широко применяется в физике, медицине, технологии создания оптических приборов и устройств.
- Графика и компьютерное зрение: Лучи используются для моделирования и визуализации трехмерных объектов. Техника трассировки лучей позволяет создавать реалистичные изображения, алгоритмы компьютерного зрения используют лучи для анализа и распознавания объектов на изображениях.
- Акустика: Лучи звука используются для моделирования и анализа распространения звуковых волн в пространстве. Они помогают определить направление звука и его взаимодействие с окружающей средой.
- Математическая геодезия: Лучи используются для измерения расстояний и углов в геодезии. Они помогают определить положение точек на земной поверхности, а также строить карты и планы.
Это только некоторые области, в которых лучи играют важную роль. Их применение может быть очень разнообразным и широким, и они продолжают использоваться для решения различных математических и научных задач.
Геометрические конструкции с использованием лучей
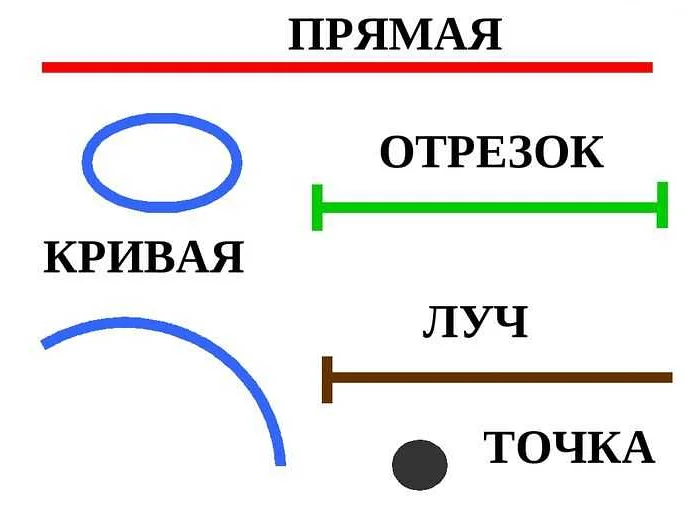
- Построение перпендикуляра к отрезку с помощью луча. Для этого нужно провести луч из одного конца отрезка так, чтобы он пересекался с прямой, содержащей отрезок, под прямым углом.
- Построение равного угла с помощью луча. Для этого нужно провести два луча с общим началом и равными углами между ними.
- Построение удвоенного угла с помощью луча. Для этого нужно провести два луча с общим началом и углом, равным половине удвоенного угла.
- Построение параллельных прямых с помощью лучей. Для этого нужно провести два луча, параллельных друг другу, к прямой исходной прямой.
- Построение треугольника с заданными сторонами с помощью лучей. Для этого нужно провести три луча, каждый из которых будет пересекаться с другими двумя в точках, расположенных на заданных расстояниях от начала луча.
Это лишь некоторые примеры того, как можно использовать лучи для геометрических конструкций. Лучи могут быть полезными инструментами для решения разнообразных геометрических задач и строительства различных фигур.
Вопрос-ответ:
Зачем нужны лучи в математике?
Лучи в математике используются для описания прямых линий, которые имеют определенное начало, но не имеют конца. Они помогают нам понять и изучить свойства и взаимодействия прямых линий.
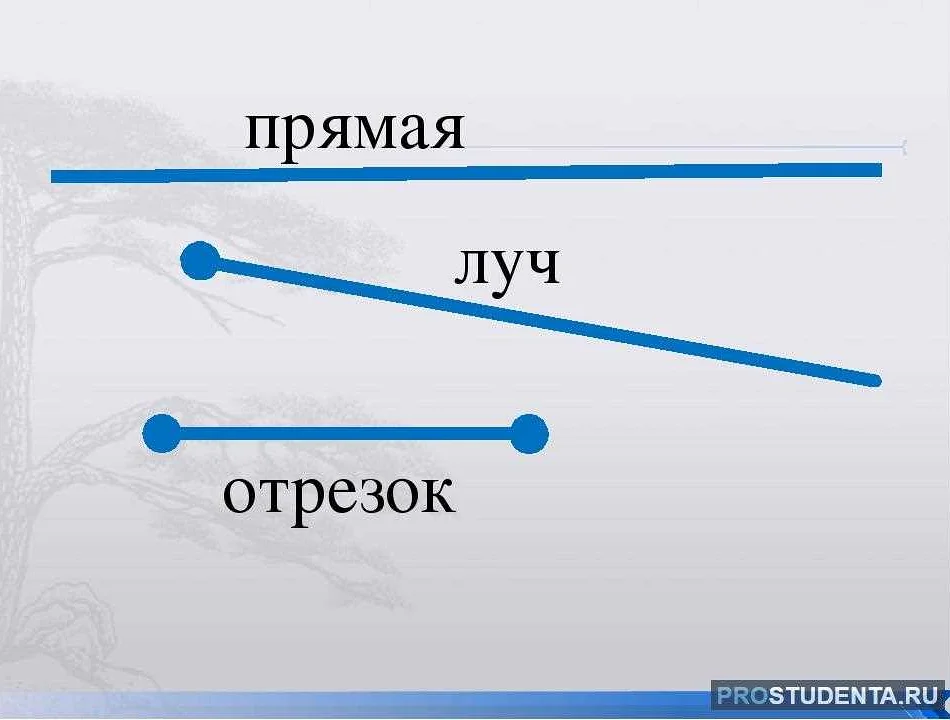
Как можно представить луч графически?
Луч можно представить графически в виде отрезка прямой линии, у которого один конец обозначен точкой, а другой конец не имеет конечной точки. Таким образом, луч будет выглядеть как полуоткрытая стрелка.
Какие бывают типы лучей?
В математике выделяют три типа лучей: луч вправо, луч влево и нулевой луч. Луч вправо имеет начало в точке и продолжается вправо до бесконечности. Луч влево имеет начало в точке и продолжается влево до бесконечности. Нулевой луч имеет только начало, но не имеет продолжения.
Можно ли нарисовать луч, который начинается с отрицательной точки?
Да, можно нарисовать луч, который начинается с отрицательной точки. Например, луч влево может начинаться из отрицательной точки и продолжаться влево до бесконечности.
Какие свойства имеют лучи?
Лучи в математике обладают несколькими свойствами. Одно из них — любая точка на луче может быть отмечена одним числом, называемым координатой точки на луче. Также лучи могут пересекаться и образовывать углы.
Что такое луч в математике?
Луч — это прямая линия, которая начинается в одной точке и продолжается бесконечно в одном направлении.
Как можно представить луч в математике?
Луч можно представить как часть прямой линии, начинающейся в одной точке и продолжающейся в одном направлении до бесконечности. В геометрии луч обозначается точкой, из которой он начинается, и стрелкой, указывающей направление.
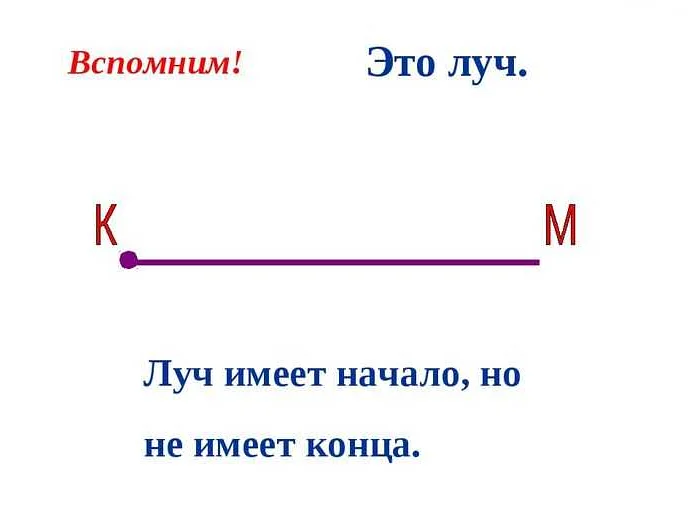


Отличная статья! Мне всегда было интересно, что такое луч в математике. Теперь я наконец разобралась! Оказывается, луч — это часть прямой, которая начинается в одной точке и простирается бесконечно в одном направлении. Это так просто объяснить, но в то же время так важно для понимания геометрии. Теперь я понимаю, как использовать лучи для решения задач и проведения различных конструкций. Спасибо за доступное и понятное объяснение! Теперь я гораздо увереннее в своих знаниях математики.
Статья очень хорошо объясняет, что такое луч в математике. Раньше я всегда путала луч с прямой, но теперь все стало понятно. Луч — это часть прямой, которая имеет начальную точку и расширяется в одном направлении до бесконечности. Такое простое объяснение очень помогло мне разобраться в этой теме. Статья написана доступным языком, что позволяет даже людям без математического образования понять это понятие. Теперь я буду точно знать, что такое луч и как его использовать при решении задач. Большое спасибо автору за такое понятное объяснение!
Отличная статья! Наконец-то я понял, что такое луч в математике. Раньше всегда путал его с прямой или отрезком. Теперь все стало ясно. Луч — это прямая линия, которая начинается в одной точке и продолжается бесконечно в одном направлении. Вот так просто! Теперь я смогу легко решать задачи, связанные с лучами, и понимать, как они работают. Спасибо автору за доступное объяснение! Читал с удовольствием и советую всем, кто хочет разобраться в этой теме.
Отличная статья! Я никогда не понимала, что такое луч в математике, но благодаря этому объяснению, все стало на свои места. Луч — это своего рода «лазерный» путь, который начинается с определенной точки и продолжается в бесконечность. Теперь я понимаю, что луч может быть направлен в любом направлении и иметь любую длину. Это так просто и логично! Теперь я буду использовать это знание в своей повседневной жизни. Спасибо вам за такое понятное объяснение! Я с нетерпением жду новых статей от вас.