Что такое равно в математике

Равно в математике – это математический символ, обозначающий равенство двух чисел, выражений или объектов. Равенство означает, что то, что находится слева от знака равно, имеет ту же самую величину или значение, что и то, что находится справа от знака. Равенство является одной из основных операций в математике и используется для сравнения чисел и выражений.

В математике равенство — это концепция, которая описывает отношение между двумя выражениями или значениями. Когда два выражения или значения равны, это означает, что они представляют одно и то же количество или количество.

В математике равенство обозначается символом «=», который разделяет два выражения или значения, которые сравниваются. Левая часть выражения или значения находится слева от символа «=», а правая часть — справа от символа «=». Если оба выражения или значения равны, они записываются таким образом: «выражение 1 = выражение 2» или «значение 1 = значение 2».

Например, если у нас есть выражение «2 + 3 = 5», это означает, что сумма чисел 2 и 3 равна 5. В этом примере «2 + 3» — это левая часть выражения, «5» — правая часть выражения, а «=» — символ равенства, который связывает их.

Равенство играет важную роль в математике и используется во многих различных областях, включая алгебру, геометрию и анализ. Понимание концепции равенства помогает нам решать уравнения, строить графики функций и проводить логические рассуждения.

Равенство в математике: определение и смысл

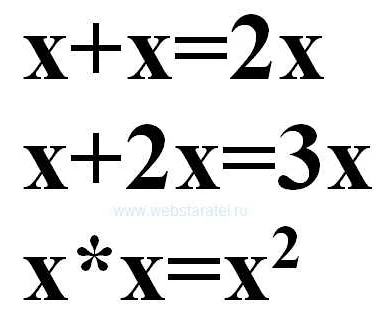
Определение равенства в математике заключается в том, что два выражения или значения считаются равными, если они имеют одинаковое значение или представляют одно и то же.

Равенство может быть использовано в различных математических операциях и уравнениях. Например, в уравнении «2 + 2 = 4» обе части уравнения равны 4, что означает, что при сложении 2 и 2 получается 4.

Смысл равенства в математике состоит в том, что оно позволяет утверждать, что два объекта или значения идентичны или эквивалентны друг другу. Равенство позволяет сравнивать и сопоставлять различные математические объекты и операции, и устанавливать их свойства и связи.

Равенство является одним из основных инструментов математики, который используется для доказательства теорем, решения уравнений и построения математической логики. Благодаря равенству мы можем утверждать, что два объекта или значения идентичны или имеют одинаковую природу, что позволяет нам изучать и понимать различные аспекты и закономерности в математике.

Равенство как математическое понятие

Основное свойство равенства – симметричность. Это означает, что если две величины равны между собой, то можно поменять их местами и равенство останется верным. Например, если «a = b», то также верно и «b = a».

Равенство может применяться к различным объектам в математике. Например, числам, переменным, алгебраическим выражениям, уравнениям и т.д. Важно знать, что равенство не всегда означает идентичность объектов. Два разных объекта могут иметь одинаковое значение в определенном контексте, и поэтому они будут считаться равными. Например, «2/4» и «1/2» – разные дроби, но они равны, так как имеют одинаковое математическое значение.

Равенство является знаком сравнения, который используется для формулировки математических утверждений и решения уравнений. Математические операции, такие как сложение, вычитание, умножение и деление, также основаны на понятии равенства.

Равенство в математических уравнениях

Математическое равенство обозначается знаком «=». Например, уравнение 2 + 2 = 4 гласит, что сумма двух чисел 2 и 2 равна числу 4.

В математических уравнениях равенство может использоваться для определения неизвестных величин. Например, в уравнении 3x = 9 равенство указывает на то, что произведение числа 3 и неизвестной величины x равно 9. В результате можно найти значение x, которое равно 3.

Равенство в математических уравнениях может быть использовано для решения различных задач и определения значений переменных или неизвестных величин.

Важно: равенство в математических уравнениях означает, что обе стороны уравнения имеют одинаковое значение. Если обе стороны не равны, то уравнение считается неверным.

Примеры:

Уравнение 5 + 3 = 8 гласит, что сумма чисел 5 и 3 равна 8. Обе стороны имеют одинаковое значение, поэтому уравнение верно.

Уравнение 2 * 4 = 10 указывает на то, что произведение чисел 2 и 4 равно 10. Обе стороны не равны, поэтому уравнение неверно.

Уравнение x + 2 = 7 указывает на то, что сумма неизвестной величины x и числа 2 равна 7. Путем вычислений можно определить, что x = 5. Обе стороны имеют одинаковое значение, поэтому уравнение верно.

Равенство в математических неравенствах

Однако, равенство также может использоваться в математических неравенствах. Неравенства устанавливают отношение между двумя выражениями и определяют, является ли одно выражение больше, меньше или равным другому.

В неравенствах с равенством используется знак «=», чтобы обозначить, что одно выражение равно другому. Например, в неравенстве «2x + 5 = 10» переменная «x» имеет значение, при котором левая часть равна правой части.

При решении неравенств с равенством нужно учитывать, что значения переменных могут быть ограничены. Если неравенство имеет вид «2x + 5 = 10», то решением будет единственное значение переменной «x», которое удовлетворяет равенству.

Таким образом, использование равенства в математических неравенствах позволяет определить точное значение переменной, при котором неравенство становится равенством.

Равенство и алгебраические операции

Алгебраические операции, такие как сложение, вычитание, умножение и деление, могут быть применены к выражениям, содержащим равенство. При этом необходимо сохранять равенство с обеих сторон. Например, если дано равенство a = b, то можно выполнить операцию сложения с обеих сторон равенства: a + c = b + c. В результате получится новое равенство, в котором все члены сложения равны.

Алгебраические операции также могут быть применены к равенству с использованием других операций. Например, если даны два равенства: a = b и c = d, то можно выполнить операцию сложения этих равенств: a + c = b + d. В результате получится новое равенство, в котором все члены сложения равны.

При выполнении алгебраических операций с равенствами необходимо учитывать особенности каждой операции. Например, при умножении равенства на число необходимо умножить каждый член равенства на это число. При делении равенства на число необходимо разделить каждый член равенства на это число. При выполнении алгебраических операций с равенствами также необходимо учитывать правила алгебры и применять их соответствующим образом.

Равенство и алгебраические операции являются важной частью математики и используются в различных областях, включая алгебру, геометрию, физику и другие науки. Понимание равенства и умение применять алгебраические операции с равенствами позволяют решать разнообразные математические задачи и строить сложные математические модели.

Равенство в геометрии и алгебре

В математике равенство играет важную роль не только в алгебре, но и в геометрии. Равенство в геометрии означает, что две фигуры или объекты имеют одинаковую форму, размеры или свойства.

В геометрии равенство может применяться к различным фигурам, таким как треугольники, прямоугольники, круги и многое другое. Например, если два треугольника имеют одинаковые длины сторон и одинаковые углы, они считаются равными.

В алгебре равенство используется для сравнения выражений и уравнений. Если два выражения или уравнения имеют одинаковые значения или равные коэффициенты, они считаются равными. Например, выражение 2 + 3 равно 5, а уравнение 2x + 5 = 15 имеет решение x = 5.

Примеры равенства в геометрииПримеры равенства в алгебре

Два прямоугольника с одинаковыми сторонами	2 + 3 = 5
Два круга с одинаковыми радиусами	2x + 5 = 15
Два треугольника с одинаковыми углами	3x + 2 = 8

Равенство в геометрии и алгебре является одним из основных понятий математики и играет важную роль в решении задач и доказательствах теорем. Понимание равенства позволяет нам устанавливать связи между различными объектами и оперировать ими в математических выкладках.

Равенство в теории множеств и логике

Для обозначения равенства в математике используется знак «=». Например, если у нас есть два числа «a» и «b», и они равны, то мы можем записать это следующим образом: a = b.

В теории множеств равенство определяется через понятие равных множеств. Множества считаются равными, если они содержат одни и те же элементы. Например, если у нас есть два множества A = {1, 2, 3} и B = {3, 2, 1}, то они считаются равными, так как содержат одни и те же элементы.

В логике равенство используется для сравнения двух выражений или формул. Если два выражения или формулы равны, то это означает, что они имеют одинаковое значение или истинность. Например, если у нас есть два выражения x + 2 = 5 и 3 = 5 — x, то они равны, так как оба выражения равны 5 при любом значении переменной x.

Равенство в теории множеств и логике играет важную роль при решении математических задач, формулировании и доказательстве теорем, а также при работе с алгебраическими и логическими операциями.

Примеры равенств в математике

В математике равенство представляет собой утверждение о равенстве двух выражений или чисел. Равенство обозначается символом «=», который означает, что выражения или числа находятся на одном уровне и имеют одинаковое значение. Вот несколько примеров равенств в математике:

ПримерРавенство

2 + 2	= 4
x + y	= z
3 * 5	= 15
a^2 + b^2	= c^2

В этих примерах левая часть выражения, разделенная символом «=», равна правой части. Например, в первом примере «2 + 2» равно «4», а во втором примере «x + y» равно «z». Равенство используется для сравнения значений и решения уравнений.

Знание равенств в математике важно для понимания основных концепций и методов решения задач. Равенство позволяет проводить операции с выражениями и числами, учитывая их равенство или неравенство. При решении уравнений равенство играет ключевую роль, позволяя находить значения переменных или неизвестных величин.

Видео по теме:

Что такое равенство в математике?

Равенство — это математическое понятие, которое означает, что два выражения или объекта имеют одинаковую величину или значение. Если два выражения или объекта равны, то их можно заменить друг на друга в любом математическом выражении или уравнении без изменения его истинности или значения.

Как записывается равенство в математике?

Равенство обозначается символом «=» в математических выражениях или уравнениях. Например, выражение «2 + 3 = 5» означает, что сумма чисел 2 и 3 равна 5.

Какие примеры равенства можно привести?

Примеры равенства в математике могут быть разными. Например, «2 + 2 = 4», «x^2 — 4 = 0», «sin(30°) = 0.5». Во всех этих примерах выражения слева и справа от знака равенства имеют одинаковое значение.

Что такое тождественное равенство в математике?

Тождественное равенство — это равенство, которое выполняется для любых значений переменных в выражениях или уравнениях. Например, выражение «x + y = y + x» является тождественным равенством, так как оно верно для любых значений переменных x и y.

В чем разница между равенством и эквивалентностью в математике?

Равенство — это понятие, которое означает, что два выражения или объекта имеют одинаковую величину или значение. Эквивалентность — это понятие, которое означает, что два выражения или уравнения имеют одинаковое значение или истинность, но могут иметь различную структуру или форму. Например, выражения «2 + 3» и «5» равны, так как имеют одинаковое значение, но они не эквивалентны, так как имеют различную структуру.

Что такое равно?

В математике равенство означает, что два выражения или значения одинаковы. Когда мы говорим, что A равно B, мы утверждаем, что A и B имеют одинаковое значение. Равенство обозначается знаком «=».