Символы в математике и что они означают
Содержимое
- 1 Символы в математике и что они означают
Узнайте о различных символах, используемых в математике, и их значениях. Эта статья поможет вам понять, что означают символы, такие как
Математика — это наука, в которой используются специальные символы для обозначения различных математических операций, величин и отношений. Эти символы играют важную роль в математических выражениях и формулах, помогая нам понять и описать сложные математические концепции.
Одним из наиболее распространенных символов в математике является знак «+», который обозначает сложение двух чисел. Например, если у нас есть числа 2 и 3, то их сумма будет обозначаться как 2 + 3. Знак «-» используется для обозначения вычитания, «*», или «×» — для обозначения умножения, а «/» или «÷» — для обозначения деления.
Кроме базовых математических операций, существуют и другие символы, которые используются для обозначения различных математических концепций. Например, символ «π» обозначает число пи, которое является одной из важных математических констант. Другой распространенный символ — «√», обозначающий квадратный корень.
Кроме того, в математике используются символы для обозначения отношений, таких как «>», »
Символы в математике позволяют нам точно и ясно записывать и обозначать математические концепции и операции. Изучение и понимание этих символов является важной частью математического образования и позволяет нам решать сложные задачи и проблемы.
Основные математические символы
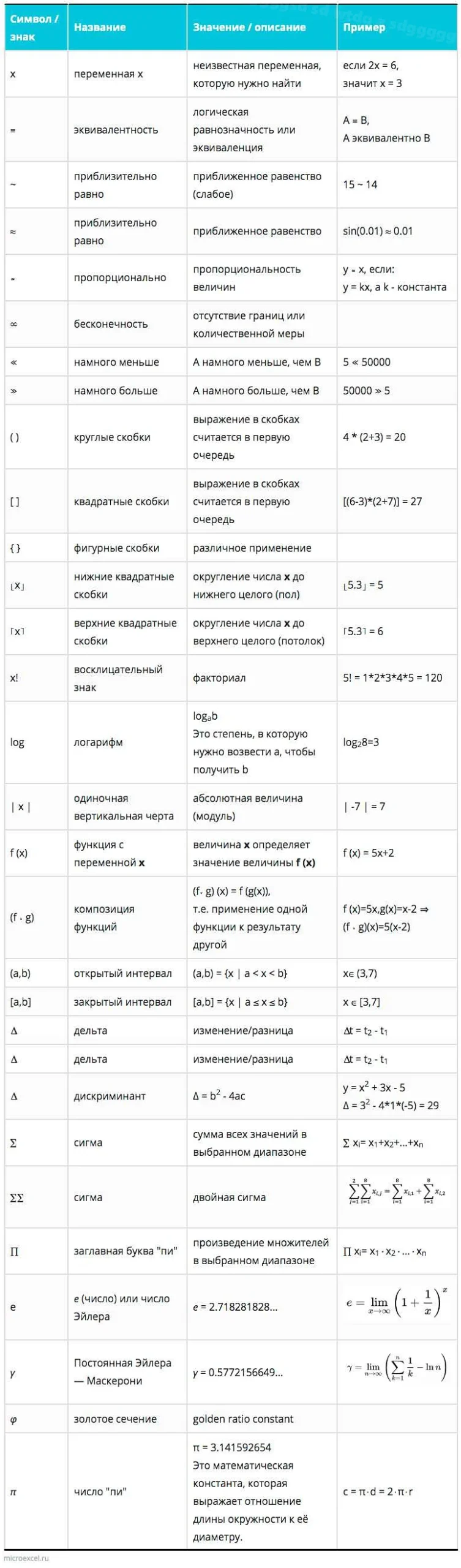
В математике существует множество символов, которые используются для обозначения различных математических операций, отношений и понятий. В этом разделе мы рассмотрим основные математические символы, их значения и использование.
Ниже приведена таблица с основными математическими символами:
СимволЗначениеИспользование
| + | Сложение | Используется для обозначения операции сложения двух чисел или выражений. |
| — | Вычитание | Используется для обозначения операции вычитания одного числа или выражения из другого. |
| × | Умножение | Используется для обозначения операции умножения двух чисел или выражений. |
| ÷ | Деление | Используется для обозначения операции деления одного числа или выражения на другое. |
| = | Равенство | Используется для обозначения равенства двух чисел или выражений. |
| < | Меньше | Используется для обозначения того, что одно число или выражение меньше другого. |
| > | Больше | Используется для обозначения того, что одно число или выражение больше другого. |
| ≤ | Меньше или равно | Используется для обозначения того, что одно число или выражение меньше или равно другому. |
| ≥ | Больше или равно | Используется для обозначения того, что одно число или выражение больше или равно другому. |
| ≠ | Не равно | Используется для обозначения того, что два числа или выражения не равны друг другу. |
Это только небольшая часть основных математических символов, которые используются в математике. Знание и понимание этих символов является важным для успешного изучения и применения математических концепций.
Символы для операций
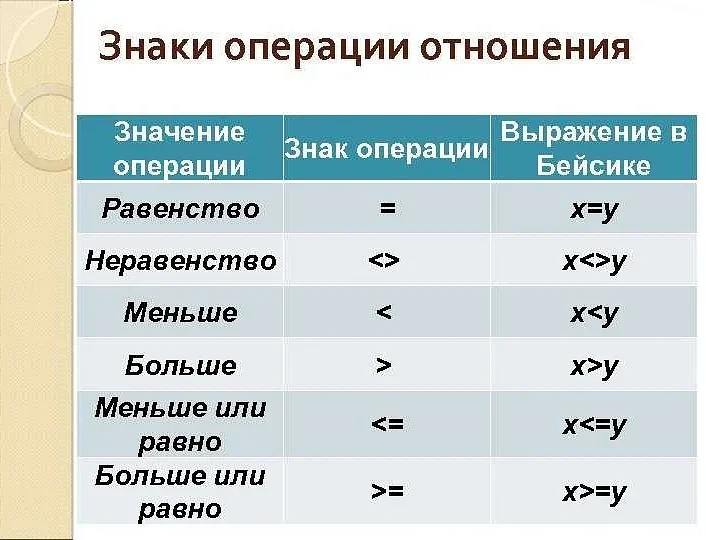
В математике существует ряд специальных символов, которые используются для обозначения различных операций. Эти символы позволяют нам записывать и прочитывать математические выражения более компактно и удобно.
Один из самых распространенных символов для операций — знак плюс «+». Он используется для обозначения сложения двух чисел. Например, выражение «2 + 3» означает сложение чисел 2 и 3.
Знак минус «-» используется для обозначения вычитания. Выражение «5 — 2» означает вычитание числа 2 из числа 5.
Знак умножения «×» используется для обозначения умножения двух чисел. Например, выражение «2 × 3» означает умножение чисел 2 и 3.
Знак деления «÷» используется для обозначения деления одного числа на другое. Выражение «6 ÷ 2» означает деление числа 6 на число 2.
Знак равенства «=» используется для обозначения равенства двух математических выражений. Например, выражение «2 + 3 = 5» означает, что сумма чисел 2 и 3 равна числу 5.
Существуют также символы для обозначения других операций, таких как возведение в степень «^», извлечение квадратного корня «√», факториал «!», процент «%», интеграл «∫», сумма «Σ» и множество других.
Знание и понимание этих символов позволяет нам легче читать и записывать математические выражения, а также решать различные задачи, связанные с математикой.
Символы для отношений

В математике существуют различные символы, которые используются для обозначения отношений между элементами. Знаки отношений позволяют выразить различные связи и сравнения между числами, множествами и другими математическими объектами.
Самым базовым символом для отношений является знак равенства (=), который обозначает, что два выражения или значения равны между собой.
Однако помимо равенства существует также множество других символов для обозначения отношений. Например, знак неравенства (≠) используется для выражения неравенства между двумя выражениями или значениями.
Другими распространенными символами для отношений являются знаки сравнения. Знаки больше (>) и меньше (<) используются для сравнения чисел или выражений и указывают на то, какое из них больше или меньше.
Знаки больше или равно (≥) и меньше или равно (≤) выражают отношение «больше или равно» и «меньше или равно» соответственно. Они указывают на то, что одно число или выражение больше или равно, или меньше или равно другому.
Символы для отношений также используются для выражения подмножества и принадлежности между множествами. Знак подмножества (⊆) обозначает, что одно множество является подмножеством другого, то есть все элементы первого множества также являются элементами второго множества. Знак принадлежности (∈) указывает, что элемент принадлежит множеству.
Символы для отношений играют важную роль в математике, позволяя выражать и изучать различные отношения и связи между математическими объектами. Умение использовать и понимать эти символы является необходимым навыком при решении задач и работы с математическими моделями.
Символы для функций
В математике символы используются для обозначения различных функций. Эти символы помогают нам описать взаимосвязи между переменными и выполнить различные операции.
Одним из наиболее распространенных символов для функций является скобка (). Она используется для обозначения аргументов функции. Например, функция f(x) обозначает, что аргументом функции является переменная x.
Еще одним распространенным символом для функций является символ равенства =. Он используется для обозначения равенства двух выражений или значений. Например, f(x) = x^2 обозначает, что функция f(x) равна x в квадрате.
Символы + и — используются для обозначения сложения и вычитания соответственно. Например, f(x) = x + 5 обозначает, что функция f(x) равна сумме переменной x и числа 5.
Символы * и / используются для обозначения умножения и деления соответственно. Например, f(x) = 2x обозначает, что функция f(x) равна удвоенному значению переменной x.
Также существуют специальные символы для обозначения определенных математических функций, таких как sin, cos, tan и др. Например, sin(x) обозначает синус переменной x, а cos(x) обозначает косинус переменной x.
Таким образом, символы для функций играют важную роль в математике, позволяя нам описывать и работать с различными функциями и их аргументами.
Символы для переменных и параметров

Буквенные символы: Одним из наиболее распространенных способов обозначения переменных является использование букв алфавита. В зависимости от контекста, эти буквы могут иметь различное значение или интерпретацию. Например, переменная «x» может обозначать неизвестное значение или координату на плоскости.
Греческие символы: В математике широко используются греческие буквы, которые обозначают различные переменные и параметры. Например, символ «α» может обозначать угол, а символ «λ» – параметр в уравнении.
Специальные символы: Кроме букв и греческих символов, в математике также используются специальные символы для обозначения определенных переменных или параметров. Например, символ «π» обозначает число «пи», а символ «∞» – бесконечность.
Индексы и верхние/нижние индексы: Иногда для обозначения переменных и параметров используются индексы или верхние/нижние индексы. Например, «x1» может обозначать первую координату на плоскости, а «a2» – квадрат числа «а».
Важно помнить, что выбор символов для переменных и параметров должен быть последовательным и ясным, чтобы избежать путаницы и ошибок при чтении и интерпретации математических выражений.
Символы для множеств и логики
Один из наиболее распространенных символов для обозначения множеств является символ «∈», который означает «принадлежит». Например, если элемент «x» принадлежит множеству «A», то можно записать «x ∈ A».
Символ «∉» обозначает «не принадлежит». Например, если элемент «y» не принадлежит множеству «B», то можно записать «y ∉ B».
Символы «⊆» и «⊂» используются для обозначения подмножества. Символ «⊆» означает, что одно множество является подмножеством другого множества, в то время как символ «⊂» означает, что одно множество является строгим подмножеством другого множества.
Символы «∪» и «∩» используются для обозначения объединения и пересечения множеств соответственно. Например, если есть множества «A» и «B», то запись «A ∪ B» означает объединение этих множеств, а запись «A ∩ B» означает пересечение этих множеств.
Для обозначения разности множеств используется символ «–». Например, запись «A – B» означает разность между множеством «A» и множеством «B».
Символ «∅» обозначает пустое множество.
В логике используются различные символы для обозначения логических операций. Символ «¬» обозначает отрицание или отрицательное утверждение. Символ «∧» обозначает логическую конъюнкцию или логическое «И». Символ «∨» обозначает логическую дизъюнкцию или логическое «ИЛИ». Символ «→» обозначает логическую импликацию или логическое «ЕСЛИ…ТО». Символ «↔» обозначает логическое равносильность или логическое «ТОГДА И ТОЛЬКО ТОГДА».
Это лишь некоторые из символов, используемых в математике для обозначения множеств и логических операций. Знание этих символов поможет лучше понимать и записывать математические выражения.
Видео по теме:
Вопрос-ответ:
Зачем в математике используются символы?
Символы в математике используются для обозначения различных математических объектов, операций и свойств. Они помогают сократить запись математических выражений и упростить их понимание.
Какие символы используются в математике?
В математике используется множество символов, таких как буквы латинского и греческого алфавита, цифры, знаки операций (плюс, минус, умножение, деление), скобки (круглые, квадратные, фигурные), индексы и многие другие.
Какие символы обозначают математические операции?
В математике используются следующие символы для обозначения математических операций: плюс (+), минус (-), умножение (× или *), деление (÷ или /), степень (^), корень (√), интеграл (∫), сумма (∑) и другие.
Какие символы используются для обозначения математических отношений и свойств?
Для обозначения математических отношений и свойств используются следующие символы: равно (=), не равно (≠), больше (>), меньше (
Символы для вероятности и статистики
В математике существует множество символов, используемых для обозначения вероятности и статистики. Эти символы помогают нам описывать и анализировать случайные события и данные.
Ниже приведены некоторые из наиболее распространенных символов, используемых в вероятности и статистике:
- P(A) — обозначает вероятность события A.
- P(A|B) — обозначает условную вероятность события A при условии, что событие B уже произошло.
- P(A∩B) — обозначает вероятность одновременного наступления событий A и B (пересечение).
- P(A∪B) — обозначает вероятность наступления хотя бы одного из событий A и B (объединение).
- P(A’) или P(Ac) — обозначает вероятность противоположного события (дополнение к событию A).
- P(A|Bc) — обозначает условную вероятность события A при условии, что событие B не произошло.
- E(X) — обозначает математическое ожидание случайной величины X.
- Var(X) — обозначает дисперсию случайной величины X.
- σ(X) — обозначает стандартное отклонение случайной величины X.
- μ — обозначает среднее значение популяции.
- N — обозначает размер популяции.
- n — обозначает размер выборки.
- x̄ — обозначает среднее значение выборки.
Это лишь некоторые из символов, используемых в вероятности и статистике. Понимание и использование этих символов позволяет нам более точно и ясно выражать наши идеи и результаты исследований.
Символы для геометрии и тригонометрии
В математике существуют различные символы, которые используются для обозначения геометрических и тригонометрических понятий. Эти символы помогают наглядно представить геометрические фигуры и отношения между ними, а также обозначить основные тригонометрические функции.
Одним из наиболее часто используемых символов для геометрии является символ «∠», который обозначает угол. Например, если есть угол АBС, то его можно обозначить как ∠ABC.
Для обозначения отрезков и отрезков прямых линий часто используются символы «-«, «=». Например, отрезок AB можно записать как AB, а отрезок AB, равный отрезку CD, можно записать как AB = CD.
Также для обозначения отношений между геометрическими фигурами используются символы «∥» (параллельность), «⊥» (перпендикулярность) и «≅» (конгруэнтность). Например, если прямая AB параллельна прямой CD, то это может быть записано как AB ∥ CD.
В тригонометрии часто используются символы для обозначения основных тригонометрических функций. Например, символ «sin» обозначает синус, «cos» — косинус, «tan» — тангенс и так далее. Символы этих функций можно записать как sin(x), cos(x), tan(x), где x — аргумент функции.
Также для обозначения специальных углов, таких как 90 градусов (прямой угол), 180 градусов (полный угол) и 360 градусов (оборот), часто используется символ «°». Например, прямой угол можно записать как 90°, полный угол — как 180°.
Использование этих символов помогает упростить запись геометрических и тригонометрических понятий и делает их более понятными и удобными для чтения.
СимволЗначение
| ∠ | Угол |
| — | Отрезок |
| = | Равенство отрезков |
| ∥ | Параллельность |
| ⊥ | Перпендикулярность |
| ≅ | Конгруэнтность |
| sin, cos, tan | Тригонометрические функции |
| ° | Градус |
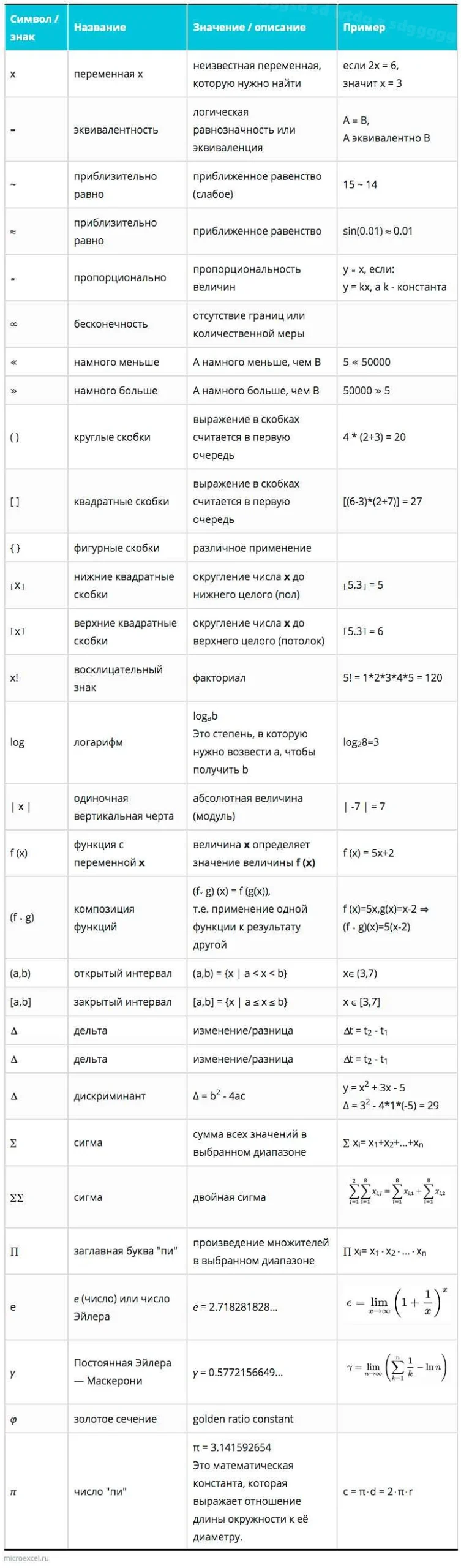


Статья очень интересная и полезная! Я всегда интересовалась математикой, и поэтому было интересно узнать о символах, которые используются в этой науке. Автор хорошо объяснил значения и использование различных символов, что поможет мне лучше понимать математические формулы и уравнения. Особенно мне понравилось, как автор рассказывает о символе «π» — это число, которое встречается во многих математических задачах и имеет особое значение. Я также узнала о других интересных символах, таких как «∑», «∫» и «≠». Эти символы используются для обозначения сумм, интегралов и неравенств соответственно. Теперь, благодаря этой статье, я смогу лучше разбираться в математических выражениях и формулах. Большое спасибо автору за такую полезную и понятную статью!