Что называют отношением математика 6 класс

Отношение в математике 6 класса — это способ связать два набора чисел или объектов. Оно может быть представлено в виде таблицы, графика или формулы. Важно уметь интерпретировать и работать с отношениями, так как они широко используются в различных областях математики и науки.

Отношение — это важное понятие в математике, которое изучается уже с 6 класса. Оно помогает нам установить или описать связь между двумя или более объектами или явлениями. Отношения применяются в различных областях науки и повседневной жизни и позволяют нам анализировать, сравнивать и классифицировать различные явления и объекты.

В математике отношения могут быть представлены различными способами, но наиболее распространенным является использование графиков и таблиц. График отношения показывает зависимость между двумя переменными и может быть представлен в виде линейного, параболического или другого типа графика. Таблица отношения позволяет увидеть соответствие между значениями двух переменных.

Примером отношения может служить зависимость между временем и расстоянием при движении автомобиля с постоянной скоростью. В этом случае, чем больше прошло времени, тем больше пройденное расстояние. Это можно представить графически или записать в виде таблицы.

Отношения играют важную роль в решении задач и построении моделей, а также в анализе данных и предсказании результатов. Понимание концепции отношений поможет учащимся развивать логическое мышление, аналитические навыки и умение применять математические методы в реальной жизни.

Что такое отношение в математике 6 класса?

В математике 6 класса основными типами отношений являются равенство, неравенство, порядок, соответствие и функция. Рассмотрим каждый из них:

1. Равенство: Отношение, которое показывает, что два объекта или выражения имеют одинаковую величину или значение. Например, 5 + 3 = 8 или 2 * 4 = 8.
2. Неравенство: Отношение, которое показывает, что два объекта или выражения имеют различные величины или значения. Например, 7 > 3 или 9 < 12.
3. Порядок: Отношение, которое показывает, что один объект или выражение больше, меньше или равно другому. Например, 5 < 9 или 10 > 7.
4. Соответствие: Отношение, которое показывает, какие элементы одного множества соответствуют элементам другого множества. Например, каждому числу от 1 до 5 можно сопоставить его квадрат: 1 — 1, 2 — 4, 3 — 9 и т.д.
5. Функция: Отношение, которое показывает зависимость одного множества (аргументов) от другого множества (значений). Каждому элементу аргументов соответствует ровно один элемент значений. Например, функция f(x) = 2x, где x — аргумент, а 2x — значение.

Знание и понимание отношений в математике 6 класса помогает решать задачи, анализировать и строить графики, а также применять математические концепции в реальных ситуациях.

Понятие отношения

Отношение может быть задано различными способами. Например, отношение между множествами «страны» и «столицы» можно представить в виде списка пар значений: [(Россия, Москва), (Франция, Париж), (Германия, Берлин)]. Это означает, что Россия связана со столицей Москва, Франция — с Парижем и Германия — с Берлином.

Отношение также может быть представлено с помощью графа, в котором элементы одного множества представлены вершинами, а связи между элементами обозначаются ребрами.

В математике 6 класса отношение может быть использовано для решения различных задач, например, для определения сходства и различия между объектами, классификации элементов, построения таблиц и графиков.

Отношение в математике позволяет строить логические связи и анализировать структуру объектов. Оно является важным инструментом для изучения различных математических концепций и решения задач.

Виды отношений

В математике 6 класса существует несколько видов отношений:

Равенство: отношение между двумя объектами, которые имеют одинаковые значения или свойства. Например, 2 + 2 = 4.

Неравенство: отношение между двуми объектами, которые имеют разные значения или свойства. Например, 3 > 2.

Сравнение: отношение между двуми объектами, которые имеют разные значения или свойства, но можно определить, какой из них больше или меньше. Например, 5 < 10.

Эквивалентность: отношение между двуми объектами, которые имеют одинаковые значения или свойства. Например, 5 метров = 500 сантиметров.

Подобие: отношение между двуми объектами, которые имеют одинаковые пропорции или формы, но могут иметь разные размеры. Например, два треугольника с одинаковыми углами, но разными размерами.

Подмножество: отношение между двуми множествами, где каждый элемент одного множества также является элементом другого множества. Например, множество {1, 2, 3} является подмножеством множества {1, 2, 3, 4, 5}.

Принадлежность: отношение между элементом и множеством, где элемент находится внутри множества. Например, число 3 принадлежит множеству {1, 2, 3}.

Эти виды отношений играют важную роль в математике и используются для решения различных задач и проблем.

Признаки отношений

Отношение между двумя множествами может быть определено по нескольким признакам:

1. Рефлексивность — отношение является рефлексивным, если каждый элемент множества A находится в отношении с самим собой. Например, отношение «быть родителем» является рефлексивным, так как каждый человек является родителем самому себе.

2. Симметричность — отношение является симметричным, если для любых двух элементов a и b из множества A, если a находится в отношении с b, то и b находится в отношении с a. Например, отношение «быть братом» является симметричным, так как если Алексей — брат Василия, то Василий — брат Алексея.

3. Транзитивность — отношение является транзитивным, если для любых трех элементов a, b и c из множества A, если a находится в отношении с b и b находится в отношении с c, то a находится в отношении с c. Например, отношение «быть предком» является транзитивным, так как если Алексей — отец Василия, а Василий — отец Игоря, то Алексей — отец Игоря.

4. Антисимметричность — отношение является антисимметричным, если для любых двух элементов a и b из множества A, если a находится в отношении с b и b находится в отношении с a, то a и b равны. Например, отношение «быть братьями» является антисимметричным, так как если Алексей — брат Василия, то Василий не может быть братом Алексея.

Эти признаки помогают определить свойства и характеристики отношений между множествами и дают возможность более полно и точно описать их в математической форме.

Отношение «больше»

Число A считается больше числа B, если A находится правее B на числовой прямой. Например, число 7 больше числа 3, потому что оно находится правее на числовой прямой.

Отношение «больше» также можно использовать для сравнения выражений и переменных. Например, выражение 2 + 3 больше выражения 1 + 4, потому что оно имеет большую сумму.

При сравнении чисел важно учитывать их знаки. Например, число -5 меньше числа -3, потому что оно находится левее на числовой прямой.

Отношение «меньше»

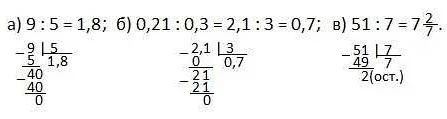
Отношение «меньше» используется для сравнения двух чисел и показывает, что одно число меньше другого. Например, если имеются числа 5 и 8, то можно сказать, что 5 меньше 8, и это записывается как 5 < 8.

Это отношение также может быть использовано для сравнения переменных или выражений. Например, если имеется выражение 2x — 3y < 7, то оно говорит о том, что значение выражения 2x — 3y меньше 7.

Отношение «меньше» имеет несколько свойств, например:

• Если a < b и b < c, то a < c. Это свойство называется транзитивностью.
• Если a < b и b < a, то a ≠ b. Это свойство называется антисимметричностью.
• Для любого числа a, не существует такого числа x, что a < x < a. Это свойство называется несравнимостью.

Отношение «меньше» широко используется в математике и имеет много применений, например, в сравнении чисел, упорядочении элементов множеств, определении границ и интервалов и т. д.

Видео по теме:

Вопрос-ответ:

Что такое отношение в математике?

Отношение в математике — это связь между двумя или более объектами, числами или событиями. Оно определяет, как один объект связан или относится к другому.

Какие примеры отношений можно привести?

Примеры отношений в математике: отношение «больше», «меньше», «равно»; отношение «включает в себя», «не включает в себя»; отношение «содержит», «не содержит» и т.д.

Как можно представить отношение между двумя числами?

Отношение между двумя числами можно представить с помощью математических знаков. Например, если число A больше числа B, то отношение между ними будет обозначаться как A > B. Если числа A и B равны, то отношение будет обозначаться как A = B.

Какие другие понятия связаны с отношением в математике?

С отношением в математике связаны такие понятия как неравенство, эквивалентность, подмножество. Они также описывают связи и отношения между объектами, числами или событиями.

Какие свойства может иметь отношение в математике?

Отношение в математике может обладать свойствами, такими как рефлексивность, симметричность и транзитивность. Рефлексивность означает, что каждый объект связан с самим собой. Симметричность означает, что если объект A связан с объектом B, то и объект B связан с объектом A. Транзитивность означает, что если объект A связан с объектом B, а объект B связан с объектом C, то объект A связан с объектом C.

Что такое отношение в математике?

Отношение в математике — это связь между двумя или более элементами или множествами. Оно может быть представлено в виде пары значений или в виде графика. Отношение может быть задано не только числами, но и другими объектами, такими как буквы или слова.

Какие примеры отношений можно привести?

В математике существует множество примеров отношений. Например, отношение «больше» или «меньше» может быть применено к числам. Если взять множество всех целых чисел, то можно сказать, что число 5 больше числа 3. Это будет отношение больше. Также можно рассмотреть отношение «прямоугольник» и «квадрат». Прямоугольник — это более общее понятие, а квадрат — это частный случай прямоугольника, у которого все стороны равны. Это будет отношение принадлежности.

Отношение «равно»

Примеры использования отношения «равно»:

Пример 1:

Если дано выражение 3 + 2 = 5, это означает, что результат сложения чисел 3 и 2 равен 5.

Пример 2:

Если дано выражение 2x + 1 = 7, это означает, что значение переменной x, при котором левая часть выражения равна правой части, равно 3.

Отношение «равно» является одним из основных отношений в математике и является основой для решения уравнений и построения математических моделей.

Примеры отношений

1. Отношение равенства: это отношение, при котором два объекта или набора объектов считаются равными. Например, если у нас есть два числа 5 и 5, то мы можем сказать, что они равны друг другу: 5 = 5.

2. Отношение неравенства: это отношение, при котором два объекта или набора объектов считаются неравными. Например, если у нас есть два числа 5 и 6, то мы можем сказать, что они не равны друг другу: 5 ≠ 6.

3. Отношение порядка: это отношение, при котором один объект или набор объектов считается больше, меньше или равным другому объекту или набору объектов. Например, если у нас есть два числа 5 и 6, мы можем сказать, что 5 меньше 6: 5 < 6.

4. Отношение принадлежности: это отношение, при котором объект считается элементом заданного набора. Например, если у нас есть набор чисел {1, 2, 3, 4, 5}, мы можем сказать, что число 3 принадлежит этому набору: 3 ∈ {1, 2, 3, 4, 5}.

5. Отношение подмножества: это отношение, при котором один набор объектов считается подмножеством другого набора объектов. Например, если у нас есть два набора чисел {1, 2, 3} и {1, 2, 3, 4, 5}, мы можем сказать, что первый набор является подмножеством второго набора: {1, 2, 3} ⊆ {1, 2, 3, 4, 5}.

Это лишь некоторые примеры отношений, которые можно встретить в математике 6 класса. Отношения играют важную роль в математике и позволяют нам описывать взаимосвязи между объектами и наборами объектов.