Что такое отношение и пропорции в математике

Отношение и пропорции — важные понятия в математике, которые позволяют сравнивать и соотносить различные величины. Узнайте, как они используются в решении задач и вычислениях, и как они могут помочь в повседневной жизни.

Отношение и пропорции являются важными понятиями в математике, которые используются для сравнения и связи между различными числами или величинами. Они помогают нам понять, как одно значение или количество связано с другим и как изменение одного значения может влиять на другие.

Отношение отражает соотношение между двумя или более значениями или величинами. Оно может быть выражено в виде дроби, где числитель представляет одно значение, а знаменатель — другое. Например, если у нас есть отношение между количеством мальчиков и девочек в классе, оно может быть выражено как 3/2, что означает, что на каждые 3 мальчика приходится 2 девочки.

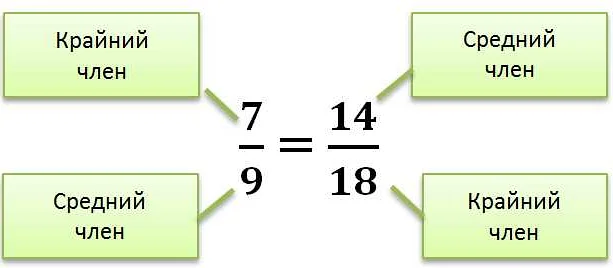
Пропорция — это особый вид отношения, где два отношения сравниваются между собой. Пропорция записывается в виде a/b = c/d, где a, b, c и d — числа или величины. Пропорция говорит нам, что отношение между a и b равно отношению между c и d. Например, если у нас есть пропорция 2/3 = 4/6, это означает, что отношение между 2 и 3 такое же, как отношение между 4 и 6.

Отношение и пропорции широко используются в различных областях, таких как физика, экономика, геометрия и т.д. Они помогают нам решать задачи, связанные с расчетами, измерениями, планированием и многими другими аспектами. Понимание основных понятий и правил отношения и пропорций является важной частью математического образования и позволяет нам лучше понять окружающий мир.

Отношение и пропорции в математике

Отношение – это сравнение двух величин, обозначаемых символом «:» или «÷». Оно показывает, сколько раз одна величина содержится в другой. Например, отношение между числами 4 и 2 можно записать как 4:2 или 4÷2, и оно равно 2. В этом случае можно сказать, что число 4 содержит число 2 два раза.

Пропорции – это равенства двух отношений. Пропорция можно записать в виде a:b = c:d или a/b = c/d, где a, b, c и d – это числа или выражения. Пропорция показывает, что два отношения равны между собой. Например, пропорция 2:4 = 1:2 означает, что отношение 2:4 равно отношению 1:2. В этом случае можно сказать, что число 2 содержится в числе 4 такое же количество раз, как число 1 содержится в числе 2.

Для работы с пропорциями существуют основные правила:

1. Произведение крайних членов пропорции равно произведению средних членов. Например, в пропорции a:b = c:d, произведение a*d будет равно произведению b*c.
2. Если крайние члены пропорции равны, то и средние члены также равны. Например, если a:b = b:c, то a = c.
3. Если средние члены пропорции равны, то и крайние члены также равны. Например, если a:b = c:b, то a = c.
4. Если крайние члены пропорции равны и средний член равен нулю, то и средний член пропорции также равен нулю. Например, если a:b = c:0, то c = 0.

Отношение и пропорции широко используются в различных областях математики и физики, а также в реальной жизни. Например, они могут применяться при решении задач на пересчет единиц измерения, расчетах соотношений в рецептах, финансовых расчетах и т.д.

Изучение отношений и пропорций позволяет более глубоко понять взаимосвязи между различными величинами и использовать их для решения различных задач и задачек.

Определение и понятие отношения

Отношение между двумя элементами обозначается символом «∼». Если элементы A и B находятся в отношении ∼, то можно записать A ∼ B. Отношение может быть различного типа, например, равенства, неравенства, сравнения и прочие.

Отношение также может быть представлено в виде таблицы, называемой матрицей отношений. В этой таблице строки соответствуют элементам одного множества, а столбцы — элементам другого множества. Каждый элемент таблицы указывает, находится ли соответствующая пара элементов в отношении или нет.

B
C
D
AE

да	нет	да
да	да	нет

В приведенной таблице элемент A связан с элементом B, но не связан с элементом C и снова связан с элементом D. Элемент E связан и с B, и с C, но не связан с D.

Отношение играет важную роль в математике и других науках, так как позволяет анализировать и описывать связи между различными объектами и явлениями. Понимание отношения и его свойств помогает решать задачи и строить логические цепочки утверждений на основе имеющихся предпосылок.

Пропорции в математике

Пропорция записывается с использованием знака равенства и двух двоеточий. Например, A:B::C:D, где A, B, C и D – это величины.

Пропорция можно решить с помощью кросс-метода или применения правила трех. Кросс-метод заключается в перемножении диагональных элементов и приравнивании полученных произведений. Правило трех позволяет найти одну неизвестную величину, используя две известные и уже найденную третью.

Пропорции применяются в различных областях математики, физики, экономики и других науках. Они являются основой для решения задач, связанных с пропорциональными зависимостями и сравнением величин.

Пропорции в математике позволяют находить неизвестные значения и устанавливать соотношения между различными величинами.

Основные правила отношений

В математике существуют несколько основных правил отношений, которые позволяют выполнять различные операции с отношениями:

• Умножение отношений: При умножении отношений, числитель одного отношения умножается на числитель другого отношения, а знаменатель одного отношения умножается на знаменатель другого отношения. Получившиеся числитель и знаменатель являются числителем и знаменателем нового отношения соответственно.
• Деление отношений: При делении отношений, числитель первого отношения умножается на знаменатель второго отношения, а знаменатель первого отношения умножается на числитель второго отношения. Получившиеся числитель и знаменатель являются числителем и знаменателем нового отношения соответственно.
• Сложение и вычитание отношений: При сложении или вычитании отношений, необходимо привести их к общему знаменателю и затем сложить или вычесть числители. Получившийся числитель и знаменатель являются числителем и знаменателем нового отношения соответственно.

Эти правила позволяют выполнять различные операции с отношениями и преобразовывать их для удобства математических расчетов.

Как вычислить отношение и пропорцию

Для вычисления отношения между двумя числами, необходимо разделить первое число на второе число. Например, если у нас есть два числа, 4 и 2, отношение между ними будет равно 4/2 = 2.

Чтобы вычислить пропорцию, необходимо иметь четыре числа, которые образуют две пары пропорциональных значений. Пропорция записывается в виде a/b = c/d. Чтобы вычислить неизвестное значение в пропорции, можно использовать правило трех. Например, если у нас есть пропорция 2/3 = x/6, для вычисления значения x необходимо умножить 2 на 6 и разделить полученное число на 3. Таким образом, x = (2*6)/3 = 12/3 = 4.

Важно помнить, что при вычислении пропорций необходимо сохранять равенство между отношениями чисел в каждой паре. Если одна из пар чисел не подчиняется этому равенству, то пропорция считается неверной и ее нельзя использовать для вычисления.

Таким образом, для вычисления отношения и пропорции в математике необходимо использовать определенные правила и формулы. Эти понятия широко используются в различных областях, таких как физика, экономика, геометрия и другие, и играют важную роль в решении различных задач.

Применение отношений в реальной жизни

Пропорции могут быть использованы, например, при расчете доли составляющих в смеси. Если нам известно, что вещество А составляет 20% от общего объема смеси, а вещество Б — 30%, то можно с помощью пропорций определить, какой объем смеси занимают каждое из веществ.

Отношения также применяются при решении финансовых задач. Например, при расчете процентов. Если известно, что вклад в банке увеличивается на 5% ежегодно, то с помощью отношений можно определить, какая сумма будет находиться на счету через определенное количество лет.

Отношения и пропорции также используются в строительстве. Например, при проектировании зданий и сооружений. Зная размеры одной части объекта, можно с помощью пропорций определить размеры других частей.

В области медицины отношения и пропорции используются при расчете доз лекарств. Зная, сколько миллиграммов содержится в одной таблетке, можно с помощью пропорций определить, какую дозу лекарства нужно принять.

Применение отношений и пропорций помогает нам более точно анализировать и понимать мир вокруг нас. Они позволяют решать различные задачи, связанные с сравнением и зависимостью величин, и находить практические решения.

Видео по теме:

Вопрос-ответ:

Какие основные понятия связаны с отношением и пропорцией в математике?

Основными понятиями, связанными с отношением и пропорцией, являются отношение, пропорция, пропорциональность, коэффициент пропорциональности и равенство отношений.

Что такое отношение в математике?

Отношение в математике — это связь между двумя или более числами, объектами или явлениями. Отношение может быть выражено с помощью дроби, где числитель и знаменатель представляют собой соответствующие элементы отношения.

Как определить пропорцию?

Пропорция — это равенство двух отношений. Пропорция можно записать в виде a/b = c/d, где a, b, c и d — числа или выражения. Если пропорция истинна, то она остается истинной при перестановке числителей и знаменателей или при умножении или делении всех частей на одно и то же ненулевое число.

Что такое пропорциональность?

Пропорциональность — это свойство отношения или пропорции, когда два или более отношения имеют одинаковые значения. Если отношение a/b равно отношению c/d, то эти отношения пропорциональны.

Что такое коэффициент пропорциональности?

Коэффициент пропорциональности — это число, которое связывает два пропорциональных отношения. Он определяется отношением значений соответствующих элементов пропорции. Если пропорция a/b = c/d верна, то коэффициент пропорциональности равен a/c = b/d.

Какие основные понятия связаны с отношением и пропорцией в математике?

Основными понятиями, связанными с отношением и пропорцией, являются отношение, пропорциональность, пропорциональные отношения и пропорциональные величины.

Что такое отношение в математике?

Отношение — это сравнение двух величин или чисел, обозначаемое символом «:», который читается как «к», «в», «из» или «равно». Например, отношение 3:5 означает, что одно число в 3 раза меньше другого.

Отношения и пропорции в геометрии

Отношение – это сравнение двух величин или свойств. В геометрии отношения часто используются для сравнения длин отрезков или площадей фигур. Например, можно сравнить длину одной стороны треугольника со стороной другого треугольника.

Пропорция – это равенство двух отношений. Пропорции часто возникают при сравнении длин, площадей или объемов фигур. Например, если две прямые линии образуют параллельные отрезки, то отношение длин этих отрезков будет равно отношению длин других параллельных отрезков.

В геометрии существуют основные правила работы с отношениями и пропорциями:

• Правило равенства отношений: Если два отношения равны, то они равны и величины, которые они сравнивают.
• Правило суммы и разности отношений: Сумма или разность двух равных отношений также является равным отношением.
• Правило произведения и деления отношений: Произведение или частное двух равных отношений также является равным отношением.
• Правило замены величин: Если две величины в отношении заменяются на две другие величины, то отношение остается неизменным.
• Правило пропорциональности: Если отношение двух величин равно отношению двух других величин, то эти величины пропорциональны.

Понимание и умение работать с отношениями и пропорциями в геометрии позволяют решать задачи по нахождению неизвестных величин или устанавливать связи между различными фигурами.

Отношения и пропорции в алгебре

Пропорции – это особый вид отношений, в которых отношение одних величин к другим остается постоянным. Пропорции часто используются для решения задач, связанных с расчетом неизвестных величин.

В алгебре отношения и пропорции играют ключевую роль при решении уравнений и систем уравнений. Они позволяют установить связь между различными переменными и найти значения неизвестных величин.

При работе с отношениями и пропорциями в алгебре необходимо учитывать следующие правила:

1. Если два отношения равны, то их произведения также равны.
2. Если два отношения имеют одинаковую долю или одинаковую разность, то они равны.
3. Если два отношения пропорциональны, то их произведения равны.
4. Если два отношения пропорциональны, то их сумма и разность также пропорциональны.
5. Если два отношения пропорциональны, то их обратные величины также пропорциональны.

Знание основных понятий и правил работы с отношениями и пропорциями в алгебре позволяет успешно решать различные задачи и задачки, связанные с расчетами и моделированием в реальных ситуациях.