Что не является законом математической логики
Содержимое
- 1 Что не является законом математической логики
- 1.1 Абсолютная истина и ложь
- 1.2 Парадоксы и дилеммы
- 1.3 Интуиция и эмоции
- 1.4 Субъективные оценки и предпочтения
- 1.5 Нечеткие и неопределенные понятия
- 1.6 Аналоговые системы и приближения
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Какие понятия не подпадают под законы математической логики?
- 1.8.0.2 Может ли интуиция противоречить математической логике?
- 1.8.0.3 Какие аргументы не могут быть доказаны с помощью математической логики?
- 1.8.0.4 Могут ли математические теоремы быть ошибочными?
- 1.8.0.5 Есть ли ограничения у математической логики?
- 1.8.0.6 Что такое математическая логика?
- 1.9 Неадекватность математических моделей
- 1.10 Социальные и культурные влияния
Статья рассказывает о том, что не является законом математической логики и приводит примеры ошибочных утверждений и неверных выводов, которые не соответствуют правилам математической логики.
Математическая логика является одной из основных дисциплин математики, которая изучает законы и правила рассуждений. Она позволяет строить точные и формальные доказательства, а также анализировать и выявлять ошибки в рассуждениях. Однако, существуют некоторые явления и объекты, которые не могут быть охвачены математической логикой.
Одним из основных исключений из математической логики является эмоциональная сфера человека. Эмоции и чувства, такие как любовь, радость, грусть, не могут быть выражены формальными символами и правилами логики. Они являются субъективными и индивидуальными, и их описание требует использования более гибких и образных форм выражения.
Также, к исключениям из математической логики относятся некоторые философические и религиозные понятия. Например, вопрос о смысле жизни, вера в Бога или отношение к моральным ценностям не могут быть учтены и описаны математическими формулами и символами. Однако, это не делает эти понятия менее важными и значимыми для человечества.
Еще одним исключением является творчество. Математическая логика стремится к строгости и точности, в то время как творчество требует свободы мысли и нестандартных решений. Творческие процессы, такие как написание музыки, создание произведений искусства или разработка новых идей, не могут быть описаны и обоснованы математической логикой.
Абсолютная истина и ложь
Абсолютная ложь, наоборот, означает, что высказывание является ложным в любых условиях. Например, высказывание «1 + 1 = 3» является абсолютной ложью, так как оно неверно независимо от контекста и ситуации.
В математической логике трудно найти примеры абсолютной истины или лжи, так как большинство математических высказываний зависят от определенных условий и аксиом. Однако, существуют некоторые общие принципы, которые считаются абсолютно истинными или ложными.
Например, принцип исключения третьего утверждает, что любое высказывание либо истинно, либо ложно, без третьего варианта. Этот принцип считается абсолютно истинным в математической логике.
С другой стороны, принцип противоречия утверждает, что нельзя одновременно утверждать и отрицать одно и то же высказывание. Этот принцип также считается абсолютно истинным в математической логике.
Однако, в реальном мире абсолютная истина и ложь могут быть достаточно сложными и спорными концепциями. В различных областях знаний существуют разные точки зрения и подходы к определению истины и лжи. Например, в философии существует множество теорий исстинности, таких как корреспондентская теория исстинности, когерентная теория исстинности и другие.
Таким образом, абсолютная истина и ложь являются важными понятиями в математической логике, но их применение и интерпретация могут различаться в разных контекстах и областях знаний.
Парадоксы и дилеммы
Математическая логика, несмотря на свою строгость и точность, сталкивается с некоторыми интересными парадоксами и дилеммами, которые нарушают некоторые основные принципы логики.
ПарадоксОписание
| Парадокс лжеца | Это известный парадокс, в котором утверждение «Это предложение ложно» приводит к парадоксальной ситуации, когда невозможно определить, истинно ли оно или ложно. |
| Парадокс Рассела | Возникает, когда рассматривается множество всех множеств, которые не содержат самих себя в качестве элемента. Вопрос заключается в том, должно ли это множество содержаться в самом себе или нет. |
| Дилемма заключенного | Это классический парадокс из теории игр, где двум заключенным предлагается сделать выбор между сотрудничеством или изменой другому заключенному. Результаты выбора зависят от того, какой выбор сделает другой заключенный. |
| Парадокс Барбера | История о барбере, который бреет всех тех и только тех людей, которые не бреются сами. Такая ситуация приводит к парадоксу: кто же бреет барбера? |
| Парадокс Берри | В этом парадоксе рассматривается множество всех натуральных чисел, которые не могут быть описаны с помощью конечного числа слов. Вопрос заключается в том, может ли это множество быть описано конечным числом слов. |
Эти парадоксы и дилеммы вызывают интерес и споры в математическом сообществе, исследователи постоянно пытаются разрешить их и найти новые способы применения логики.
Интуиция и эмоции
Эмоции также не учитываются в математической логике. Эмоции — это сложные психологические процессы, которые включают в себя переживания, чувства и настроение. Они могут оказывать влияние на наше мышление и принятие решений, но в математической логике эмоции не играют роли. Все выводы должны быть основаны исключительно на логическом рассуждении.
Таким образом, интуиция и эмоции являются исключениями из правил математической логики. В реальной жизни они играют важную роль в нашем мышлении и принятии решений, но они не применимы в математических доказательствах и рассуждениях.
Субъективные оценки и предпочтения

Математическая логика стремится работать с точными и объективными понятиями, основываясь на строгих правилах и формальных системах. Однако, в реальном мире существует множество ситуаций, когда оценки и предпочтения людей не могут быть выражены с помощью математической логики.
Субъективные оценки и предпочтения часто связаны с индивидуальными предпочтениями, эмоциями и личным опытом. Например, вопросы вкуса, красоты или стиля могут быть предметом субъективных оценок, которые не могут быть измерены или доказаны математически.
В контексте математической логики, субъективные оценки и предпочтения часто рассматриваются как исключения, так как они не могут быть подвергнуты строгому формализму и объективным правилам. Они играют важную роль в принятии решений и оценке различных аспектов нашей жизни, но не могут быть полностью охвачены математическими методами.
Субъективные оценки и предпочтения добавляют сложности в области принятия решений и моделирования систем. Однако, понимание и учет этих субъективных факторов могут помочь нам получить более полное представление о реальном мире и сделать более обоснованные решения.
Нечеткие и неопределенные понятия
Нечеткие понятия представляют собой понятия, которые не имеют четкого и однозначного определения. Они могут иметь различные степени исчерпывания и размытости. Примером такого понятия может служить понятие «высокий рост». Что именно считается высоким ростом? Для разных людей это понятие может иметь разные значения.
Неопределенные понятия, в свою очередь, являются понятиями, которые не имеют определенного значения или имеют множество возможных значений. Такие понятия часто встречаются в естественных языках и в повседневной жизни. Например, понятие «большой» может иметь разные значения в разных контекстах и в зависимости от субъективного восприятия.
Нечеткие и неопределенные понятия представляют собой сложные задачи для математической логики и требуют разработки специальных методов и инструментов для их формализации и анализа. Эти понятия также являются важными для понимания человеческого мышления и языка.
Аналоговые системы и приближения

В математической логике, основанной на дискретных значениях и символах, существуют некоторые явления и объекты, которые не могут быть полностью описаны и учтены. Эти исключения называются аналоговыми системами и приближениями.
Аналоговые системы основаны на непрерывных значениях и функциях. Такие системы могут описывать физические процессы, где переменные имеют бесконечное количество значений в заданном интервале. Например, аналоговая система может быть использована для моделирования изменения температуры воздуха в течение времени.
Приближения используются для упрощения и аппроксимации сложных или бесконечных аналоговых систем. Вместо точного описания процесса, приближения позволяют использовать более простые и понятные модели. Например, вместо точного описания падения объекта под воздействием гравитации, можно использовать приближение свободного падения, игнорируя сопротивление воздуха.
Аналоговые системы и приближения широко используются в различных областях, таких как физика, инженерия, экономика и технологии. Они позволяют упростить сложные процессы, сэкономить вычислительные ресурсы и улучшить понимание и предсказание реальных явлений.
Видео по теме:
Вопрос-ответ:
Какие понятия не подпадают под законы математической логики?
Существуют понятия, которые не подпадают под законы математической логики, такие как эмоции, вкус, запах и другие ощущения. Математическая логика предназначена для формализации рациональных мыслей и выводов, а не для описания эмоционального или субъективного опыта.
Может ли интуиция противоречить математической логике?
Да, интуиция иногда может противоречить математической логике. Интуитивные представления о мире могут быть ошибочными или неполными, и математическая логика может помочь выявить и исправить эти ошибки. Однако интуиция также может быть полезной для создания новых математических концепций и гипотез, которые затем могут быть проверены и формализованы с использованием логических методов.
Какие аргументы не могут быть доказаны с помощью математической логики?
Математическая логика может доказывать только утверждения, основанные на логических законах и аксиомах. Она не может доказать или опровергнуть утверждения, которые связаны с эмпирическими наблюдениями или субъективными мнениями. Например, математическая логика не может доказать или опровергнуть существование Бога, потому что это вопрос, относящийся к религиозным или философским убеждениям, а не к логическим законам.
Могут ли математические теоремы быть ошибочными?
Да, математические теоремы могут быть ошибочными. Хотя математическая логика стремится к строгости и точности, ошибки могут возникнуть в процессе формулировки, доказательства или применения теорем. Однако математическое сообщество имеет механизмы проверки и рецензирования, которые помогают выявить и исправить ошибки в математических работах.
Есть ли ограничения у математической логики?
Математическая логика имеет свои ограничения. Например, она не может обрабатывать неопределенность или вероятности, которые играют важную роль во многих науках и реальном мире. Она также не всегда может учесть контекст или субъективные факторы, которые могут влиять на выводы. Кроме того, математическая логика может столкнуться с проблемами бесконечности или неполноты, когда невозможно формализовать или доказать некоторые утверждения.
Что такое математическая логика?
Математическая логика — это раздел математики, который изучает формальные языки, правила вывода и доказательства. Основная задача математической логики заключается в формализации и изучении процессов рассуждения.
Неадекватность математических моделей
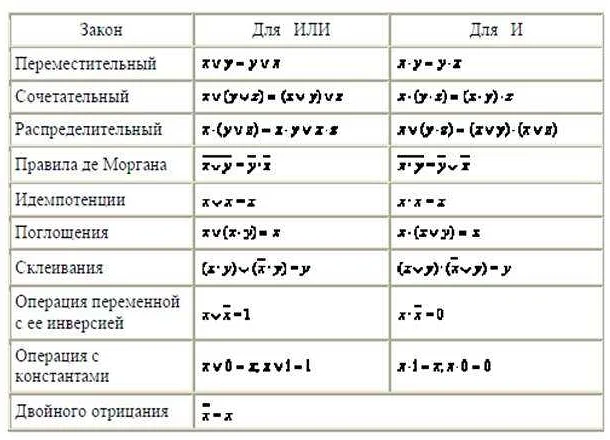
Одна из основных проблем, связанных с математическими моделями, заключается в их упрощенности. Часто модели предполагают некоторые упрощения и идеализации, что может привести к искажению реальности. Например, модель могла бы предполагать идеально гладкие поверхности или отсутствие трения, что не соответствует действительности.
Еще одной причиной неадекватности математических моделей является неучет некоторых факторов или переменных, которые могут оказывать значительное влияние на исследуемое явление. Например, модель может не учитывать влияние воздействия окружающей среды или человеческого фактора, что может существенно влиять на результаты и выводы.
Также важно отметить, что математическая модель может быть построена на основе неполной или неточной информации. В таких случаях результаты модели могут быть недостаточно точными или неправильными. Например, если данные для модели были собраны неадекватно или содержат ошибки, то результаты модели могут быть искажены.
В завершение, следует отметить, что математические модели являются всего лишь приближенным описанием реальности и не могут полностью уловить все ее аспекты. Они представляют лишь удобный инструмент для анализа и предсказания, но не являются истиной в последней инстанции.
Социальные и культурные влияния
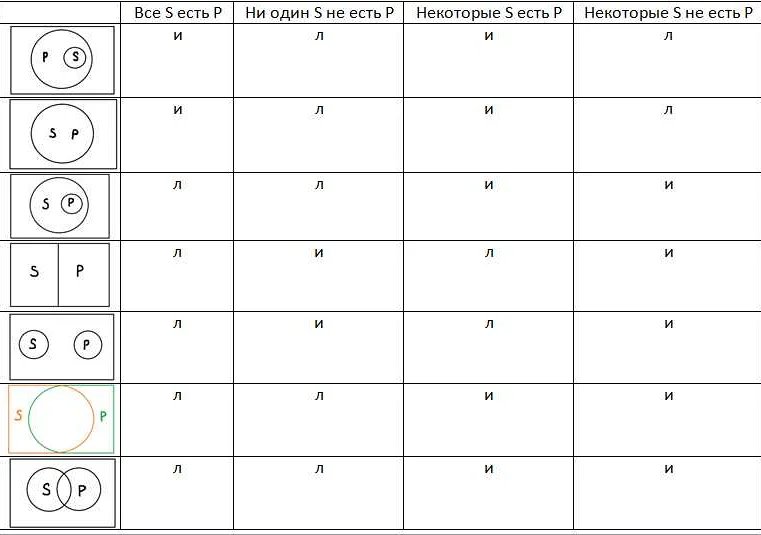
Социальное окружение и культурные нормы могут иметь значительное влияние на способ мышления и логическое рассуждение. Например, в некоторых культурах, существуют специфические логические структуры и формы рассуждений, которые отличаются от западной математической логики. Также, социальные нормы и ожидания могут повлиять на способ формулирования и восприятия логических утверждений.
Кроме того, социальные и культурные факторы могут влиять на само понимание и восприятие математической логики. В некоторых обществах, интерес к математической логике может быть низким из-за социального презрения к научным исследованиям или из-за недостатка доступности математического образования.
Таким образом, социальные и культурные факторы могут оказывать значительное влияние на понимание и использование математической логики. Эти факторы могут создавать исключения, которые необходимо учитывать при анализе и применении логических законов и правил.


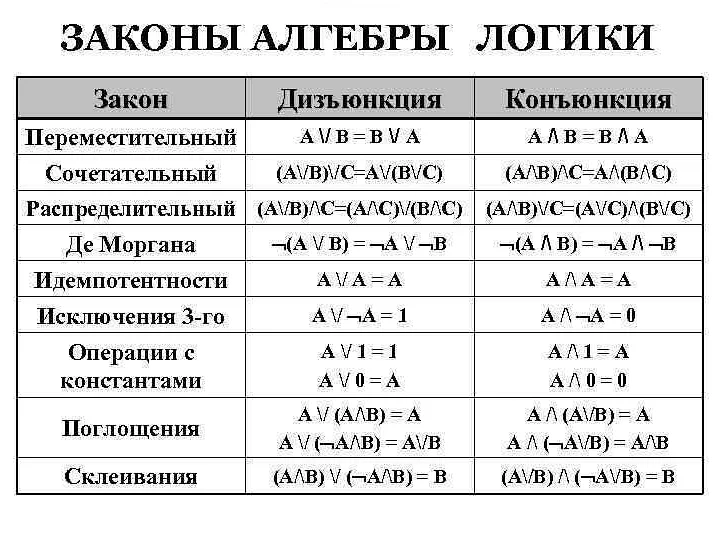


Очень интересная статья! Я всегда считал, что математическая логика применима ко всему и везде. Но оказывается, есть исключения. Например, понятие «истина» может быть неоднозначным и зависеть от контекста. Это меня поразило! Ведь мы всегда думаем, что есть только одно правильное решение. И еще одно исключение — парадокс лжеца. Как же так, когда утверждение само себе опровергает? Это противоречит всем законам логики, с которыми я знаком. Я думаю, что эти исключения делают математическую логику еще более интересной и сложной наукой. Жду продолжения!