Математическая логика в информатике: понимаем базовые концепции и применение

Математическая логика – это раздел информатики, изучающий формальные методы и правила вывода, необходимые для создания сильных и правильных алгоритмов и программ. Узнайте, зачем нужна математическая логика в информатике и как она помогает решать сложные задачи.

Математическая логика – одна из важнейших теоретических дисциплин в информатике. Она занимается изучением формальных систем, которые лежат в основе алгоритмов и вычислительных процессов. Эта наука является фундаментом ряда других дисциплин, таких как теория алгоритмов, теория формальных языков, теория вычислительных сложностей и многих других.

Все аспекты разработки программного обеспечения, от проектирования до тестирования, построены на теоретических основах математической логики. Чтобы понимать, как работают программы, как они описываются и проверяются на ошибки, необходимо знать основные понятия и методы математической логики.

В данной статье мы рассмотрим основные понятия математической логики, ее применение в информатике и значимость в разработке программного обеспечения. Опишем логические операции и связки, аксиомы и правила вывода, формальные языки и грамматики, теорию множеств и множественную логику, а также множество других важных аспектов математической логики.

Математическая логика в информатике

Математическая логика — это раздел математики, занимающийся формальным изучением структуры рассуждений и доказательств. В информатике математическая логика играет важную роль, поскольку она позволяет формализовать и выражать логические высказывания и алгоритмы в языке, понятном для компьютера.

Применение математической логики в информатике крайне широко. Одно из ее основных применений — это построение доказательств корректности программ. Также математическая логика используется при формализации языков программирования и теории алгоритмов. С ее помощью можно выразить условия и ограничения в математической форме, что упрощает автоматическую проверку программ на корректность.

Кроме того, математическая логика используется в логическом программировании, при создании экспертных систем, в искусственном интеллекте и теории баз данных. Использование формализованного языка позволяет производить автоматическую обработку информации и сокращать затраты на обработку знаний.

Наконец, математическая логика играет важную роль в разработке криптографических алгоритмов и систем защиты информации, так как позволяет формализовать свойства различных криптографических протоколов и алгоритмов, обеспечивающих конфиденциальность, целостность и аутентификацию информации.

Что такое математическая логика

Математическая логика — это раздел математики, который занимается изучением формальных языков и методов логического вывода. В математической логике исследуются свойства и структуры математических систем, описываются формальные языки, создаются методы проверки и доказательства математических теорем.

Математическая логика широко используется в информатике для разработки и анализа алгоритмов, создания логических моделей и программирования. Она является основой для построения компьютерных систем и языков программирования.

В рамках математической логики выделяют такие темы, как теория множеств, математическая индукция, формальная арифметика, моделирование искусственного интеллекта и многие другие. Она является одной из ключевых дисциплин в области информатики и представляет собой мощный инструмент для разработки новых технологий и программных продуктов.

Таким образом, понимание математической логики является важным компонентом для успешной карьеры в индустрии информационных технологий и для повышения общей математической грамотности.

История развития математической логики

Математическая логика — это раздел математики, который занимается формализацией математических выкладок и доказательств. История развития математической логики восходит к древней Греции, где философы уже задумывались над вопросом, каким образом можно формализовать логические законы и правила рассуждения.

Одним из первых, кто приложил руку к созданию формальной логики, был Аристотель. В его трудах были первые примеры формальных доказательств, а также введены понятия, которые используются и по сей день, такие как категории, силлогизмы и предикаты. В эпоху Нового времени математика и логика начали развиваться совместно, и логика перестала быть отдельной наукой, так как она была улучшена и расширена математическими методами.

Прорыв в развитии математической логики был осуществлён в XIX веке, благодаря работам Джорджа Буля. Он создал логику высказываний, в которой формулы могут быть приведены к законам алгебры исчисления высказываний. Это стало отправной точкой для создания логики предикатов, которая позволяет формулировать сложные математические теоремы в форме логических законов.

После этого возникла модальная логика, которая занимается рассуждениями о возможности и необходимости, а затем гильбертова логика, которая использует аксиомы для формализации математических теорий.

В XX веке, разработка новых типов логики, таких как интуиционистская логика, логика множеств и нестандартная логика привела к созданию новых математических теорий и понятий. И сегодня математическая логика продолжает развиваться, расширяя границы своих приложений в информатике, философии, лингвистике и других науках.

Математическая логика в информатике

Математическая логика — это раздел математики, изучающий формальную структуру и семантику языков, используемых для описания знаний и вывода новых фактов. В информатике математическая логика играет важную роль, поскольку она позволяет формализовать знания и рассуждения и использовать компьютер для их автоматического извлечения и проверки.

Математическая логика используется в информатике для создания и анализа алгоритмов, а также для проверки и доказательства корректности программ. Она также находит применение в искусственном интеллекте, где она используется для описания знаний и рассуждений и для построения экспертных систем.

Знание основ математической логики позволяет разработчикам создавать более эффективные и корректные программы. Оно также помогает ученым в области искусственного интеллекта разрабатывать более точные и надежные модели, которые могут использоваться для принятия важных решений в различных областях, таких как медицина и финансовый сектор.

Таким образом, математическая логика играет важную роль в информатике и имеет большое значение для различных областей человеческой деятельности. Ее изучение является необходимым для тех, кто стремится стать профессионалом в области информационных технологий.

Теория множеств и математическая логика

Теория множеств и математическая логика являются одними из основных областей математики, но их применение также важно для информатики. Теория множеств изучает свойства множеств и операции над ними, такие как пересечение, объединение и разность. Она используется для описания и формулирования математических понятий и законов, которые затем могут быть применены в информатике.

Математическая логика изучает формальные методы рассуждения и доказательства их истинности или ложности. Она используется для создания формальных языков и формализации математических теорий. Это позволяет анализировать и проверять их на корректность и верифицируемость.

В информатике теория множеств применяется в базах данных, которые представляют собой множества объектов, а также в алгоритмах и структурах данных, таких как множества и графы. Математическая логика используется для создания формальных языков программирования и для доказательства корректности алгоритмов.

Таким образом, теория множеств и математическая логика имеют большое значение в информатике, помогая создавать более эффективные и надежные программы и системы. Понимание этих теорий позволяет программистам более глубоко понимать принципы работы компьютерных систем и разрабатывать более сложные и продвинутые алгоритмы.

Формальные языки и математическая логика

Формальные языки – это прекрасный инструмент для описания и формализации различных явлений, начиная от естественных языков до языков программирования. Без использования формальных языков было бы трудно описывать математические и логические концепции, поскольку их можно точно определить только в пределах формальной системы.

Математическая логика, в свою очередь, является центральной областью, где используются формальные языки. Она предоставляет методы для формализации математического рассуждения, что важно в разработке программного обеспечения и во многих других областях, где требуется высокая точность формулировок и выводов.

Одним из примеров формального языка, используемого в математической логике, является язык высказываний. Он предоставляет формальное определение для логических связок, таких как «не», «и», «или», а также для кванторов, таких как «существует» и «для всех». Также с помощью языка высказываний можно определять логические формулы, состоящие из переменных и логических связок.

Кроме того, формальные языки играют ключевую роль в семантике языков программирования. Семантика является той областью, которая определяет значение языков программирования. Она использует математическую логику, чтобы формализовать семантику языков программирования. Термины и понятия, определенные на формальных языках, позволяют уточнить семантику языков программирования, сделать ее более ясной и понятной для программистов.

В целом, формальные языки и математическая логика очень важны в информатике и информационных технологиях в целом. Они представляют собой ключевые инструменты для формализации математических и логических концепций и для определения методов вычислений, что непременно приводит к созданию более эффективных систем и программного обеспечения.

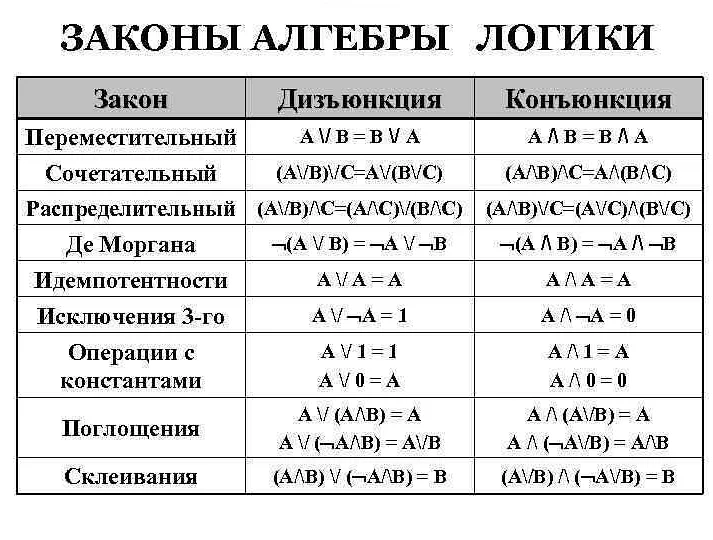
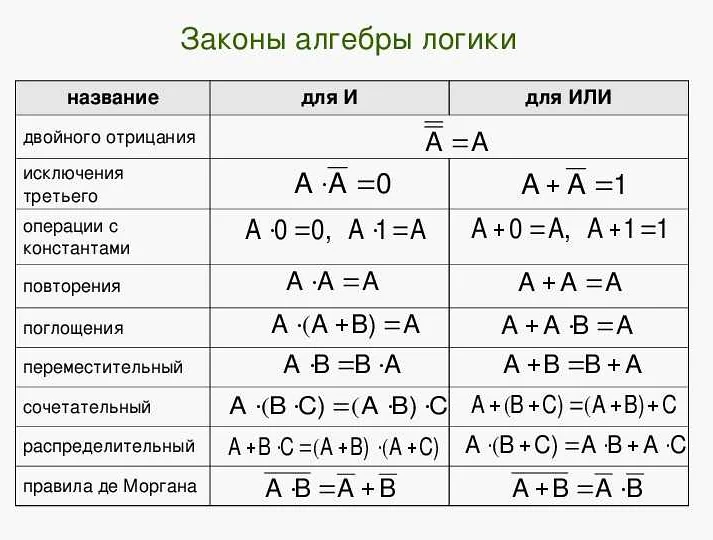
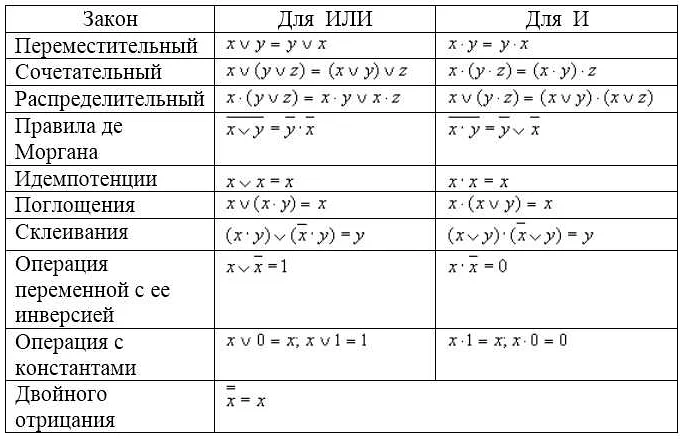
Логические операции и математическая логика

Логические операции играют важную роль в математической логике, а также в информатике. Они используются для создания логических выражений, которые позволяют программам принимать решения на основе заданных условий.

Простейшими логическими операциями являются конъюнкция (AND), дизъюнкция (OR) и отрицание (NOT). Конъюнкция и дизъюнкция принимают два логических значения и возвращают новое логическое значение в соответствии с правилами логического выражения. Отрицание, в свою очередь, принимает одно логическое значение и возвращает его противоположность.

Логические операции часто используются в условных операторах, циклах, функциях и других конструкциях программирования для создания алгоритмов принятия решений. Например, они могут использоваться для проверки правильности введенных данных или для определения, какие действия нужно выполнить в зависимости от значения переменной.

Математическая логика позволяет формализовать логические операции и выражения, упрощая их исполнение и уменьшая возможность ошибок. Благодаря использованию математической логики в программировании возможно создание сложных алгоритмов, обрабатывающих большие объемы данных и принимающих правильные решения в зависимости от ситуации.

Алгоритмы и математическая логика

Математическая логика играет ключевую роль в разработке алгоритмов и определении их корректности. Алгоритм — это последовательность действий, необходимых для выполнения определенной задачи. Когда мы пишем программу, мы создаем алгоритм для решения определенной задачи. Чтобы убедиться, что наш алгоритм работает корректно и даёт нужный результат, мы можем использовать математическую логику для формального доказательства корректности.

Математическая логика также помогает нам учиться создавать эффективные алгоритмы. Когда мы пытаемся сделать алгоритм более эффективным, мы анализируем его поведение, изменяем его и проверяем, как он работает на различных входных данных. Математическая логика помогает нам формально доказать результаты, которые мы получили в результате анализа, и проверить, что мы не ввели ошибки в свой алгоритм.

Существует множество областей, в которых математическая логика играет решающую роль в разработке алгоритмов. Например, в криптографии используются сложные алгоритмы, защищающие данные от несанкционированного доступа. Эти алгоритмы основаны на математических принципах, и для их разработки необходимо глубокое знание математической логики.

• Математическая логика позволяет формально доказать корректность алгоритма
• Она помогает создавать более эффективные алгоритмы
• Математическая логика играет ключевую роль в области криптографии

Таким образом, математическая логика является неотъемлемой частью разработки алгоритмов в информатике. Она помогает нам убедиться в корректности алгоритма, понимать, как выполнить задачу наиболее эффективно, и создавать сложные алгоритмы в области криптографии.

Применение математической логики в программировании

Математическая логика — это дисциплина, которая изучает формальную логику, основанную на математических принципах, и применение этих принципов в науках, таких как информатика и компьютерная наука. Программирование, в свою очередь, является одним из наиболее значимых и широко используемых областей информатики.

Использование математических принципов в программировании значительно упрощает процесс создания прецизионных и надежных программ. Один из ключевых элементов математической логики применяется в теории алгоритмов и решает задачи обработки данных и принятия решений в алгоритмах, которые используются в программировании.

При создании сложных программных систем, организация данных и разработка алгоритмов, основанных на математической логике, также становятся ключевыми. Использование математической логики позволяет уменьшить искажения, которые возникают в результате человеческого вмешательства и могут привести к ошибкам.

Таким образом, применение математической логики в программировании является важным элементом для разработки надежных и стабильных программных решений, которые могут быть применены в самых различных сферах деятельности, начиная от финансовых операций и заканчивая производственными процессами.

Важность математической логики для разработчиков

Математическая логика представляет собой основу многих областей информатики и является необходимой для разработки компьютерных программ. Разработчики, использующие математическую логику при написании алгоритмов и кода, могут создавать более эффективные и точные решения для сложных задач.

Математическая логика позволяет разработчикам выполнять логическое мышление при написании программного кода. Знание основ математической логики позволяет логически строить программы и минимизировать ошибки, что повышает качество и надежность приложений.

Кроме того, математическая логика является фундаментальной в области искусственного интеллекта, где использование разных формальных языков для представления знаний и логических выводов — один из центральных аспектов в разработке интеллектуальных компьютерных систем.

1. Математическая логика помогает:
2. — достичь более высокой точности в написании кода и алгоритмов;
3. — строить более эффективные решения сложных задач;
4. — минимизировать ошибки и повышать надежность программного кода;
5. — создавать системы искусственного интеллекта.

Современные направления развития математической логики в информатике

Модальная логика — одно из важнейших направлений развития математической логики в информатике. Он базируется на идеях о множестве возможных миров и допустимых утверждений в каждом из них. Модальная логика значительно сокращает количество ошибок в программировании, т.к. позволяет обрабатывать всевозможные варианты реализации программного кода.

Теория графов — другое важное направление, использующее математическую логику в информатике. Она позволяет применять графы для анализа информации, что находит широкое применение в современном мире. Это направление активно используется в поисковых системах, анализе рынка, в экономическом и социальном анализе и т.д.

Логические системы с доказательствами — это направление математической логики, которое позволяет машинам делать логические выводы на основе какой-то базовой логической системы. Это позволяет создавать искусственный интеллект, который может работать с большими объемами информации и выполнять сложные задачи с помощью формальных методов.

Теорвер — теория вероятностей и математическая статистика — это еще одно как нельзя более важное направление, на базе которого строится информатика и програмирование. Она позволяет принимать во внимание и анализировать вероятность возникновения ошибок и отклонений в работе программного обеспечения, что позволяет существенно снизить вероятность их появления. Теорвер активно применяется в областях, связанных с защитой информации и работы с большими объемами данных.

Вопрос-ответ:

Что такое математическая логика?

Математическая логика — это раздел математики, занимающийся формальным изучением законов правильного мышления. В информатике она является одной из основных дисциплин и используется для решения задач связанных с программированием, теорией алгоритмов и искусственного интеллекта.

Какую роль играет математическая логика в программировании?

Математическая логика играет ключевую роль в программировании. Она помогает разработчикам создавать алгоритмы, которые выражаются в виде логических операций, условных выражений и циклов. Без применения математической логики программисты не смогли бы создавать сложные программные продукты, например, операционные системы или приложения искусственного интеллекта.

Какие примеры применения математической логики в информатике вы можете привести?

Примеры применения математической логики в информатике включают разработку алгоритмов, моделирование программных систем, поддержку реляционных баз данных, создание и проверку формальных доказательств теорем, и многое другое. Более конкретные примеры могут включать работу с логическими операторами, принятия решений на основе булевых условий и т.д.

Как математическая логика связана с компьютерной теорией?

Математическая логика является одной из основных дисциплин компьютерной теории. Эта связь объясняется тем, что компьютерная теория занимается созданием, анализом и оптимизацией алгоритмов, которые представляют собой системы формализованных логических выражений. Без математической логики, компьютерная теория была бы бесполезной.

Какие преимущества предоставляет использование математической логики в программировании?

Использование математической логики в программировании предоставляет множество преимуществ. Она позволяет программистам создавать надежные алгоритмы, избегать ошибок в коде, уменьшать объем кода, сокращать время разработки и повышать производительность программ. Это также позволяет создавать программы с более сложными структурами и функциями, которые были бы неосуществимы без использования математической логики.

Как математическая логика влияет на процесс тестирования программных продуктов?

Математическая логика очень важна в процессе тестирования программных продуктов. Она позволяет разработчикам и тестировщикам определять, какие значения входных параметров могут привести к определенным выходным результатам и какие должны быть граничные условия для этих параметров. Математическая логика также позволяет проводить формальную проверку правильности программ, что существенно упрощает процесс тестирования.

Как математическая логика используется в искусственном интеллекте?

Математическая логика играет центральную роль в искусственном интеллекте. Она предоставляет формализованные методы для представления знаний, рассуждений, и решения сложных задач. Она также является основой для многих инструментов и методов машинного обучения, включая эволюционное программирование, нейронные сети, решение логических задач, и т.д.

Видео по теме: