Что не относится к достоинствам математического моделирования
Содержимое
- 1 Что не относится к достоинствам математического моделирования
- 1.1 Ограничения и недостатки
- 1.2 Субъективность и приближенность
- 1.3 Сложность и необходимость вычислений
- 1.4 Неучтение факторов окружающей среды
- 1.5 Неопределенность и риски
- 1.6 Ограниченность применимости
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.8.0.1 Зачем использовать математическое моделирование?
- 1.8.0.2 Какие преимущества имеет математическое моделирование?
- 1.8.0.3 Может ли математическое моделирование помочь в разработке новых продуктов?
- 1.8.0.4 Какие ограничения есть у математического моделирования?
- 1.8.0.5 Может ли математическое моделирование заменить эксперименты?
- 1.8.0.6 Какие преимущества есть у математического моделирования?
- 1.9 Зависимость от качества входных данных
- 1.10 Возможность искажения результатов
Математическое моделирование имеет свои ограничения и не является универсальным инструментом решения всех задач. Не все явления и процессы могут быть точно описаны и предсказаны с помощью математических моделей. Также важно учитывать, что математическое моделирование может быть сложным и трудоемким процессом, требующим высокой математической подготовки и специализированного программного обеспечения.
Математическое моделирование является мощным инструментом, который позволяет изучить сложные явления и процессы, предсказать их поведение и принять обоснованные решения. Однако, несмотря на множество преимуществ, существуют некоторые аспекты, которые не входят в область действия математического моделирования.
Во-первых, математическое моделирование не может полностью учесть все факторы, влияющие на изучаемое явление или процесс. В реальном мире существует множество переменных, которые могут оказывать влияние на исследуемую систему, и невозможно учесть их все в математической модели. Это ограничение может привести к недостаточно точным результатам и неправильным прогнозам.
Во-вторых, математическое моделирование не учитывает эмоциональные и социальные аспекты, которые могут оказывать влияние на принимаемые решения. Эмоции, мотивации, ценности и социальные взаимодействия людей могут существенно влиять на поведение системы и результаты моделирования. Поэтому, хотя математическое моделирование может быть полезным инструментом для принятия решений, оно не может заменить человеческий фактор и экспертное мнение.
В-третьих, математическое моделирование предполагает использование упрощенных предположений и абстракций, чтобы сделать систему более понятной и управляемой. Однако, эти упрощения могут привести к потере некоторых деталей и сложностей реальной системы. Из-за этого, результаты моделирования могут быть ограниченными и не полностью отражать реальность.
В итоге, математическое моделирование — это мощный инструмент, который позволяет изучить сложные явления и принять обоснованные решения. Однако, необходимо помнить, что оно имеет свои ограничения и не может учесть все факторы, эмоции и сложности реальной системы. Поэтому, для полного понимания и принятия решений необходимо использовать комбинацию математического моделирования и других подходов.
Ограничения и недостатки
1. Упрощение реальности: Когда математическая модель создается, неизбежно происходит упрощение реального мира. Это может привести к искаженным результатам, если модель не учитывает все факторы и взаимодействия, которые могут влиять на реальную систему.
2. Невозможность учета всех переменных: Даже если модель строится с учетом большого количества факторов, все равно существуют переменные, которые невозможно учесть. Например, неконтролируемые внешние воздействия или случайные события могут значительно изменить результаты моделирования.
3. Проблема с ограниченностью данных: Для построения математической модели требуется наличие большого объема данных. Однако, не всегда возможно получить достаточное количество точных данных для моделирования, особенно если исследуется сложная система.
4. Неполнота и неверность модели: Математическая модель может быть неполной и неверной, если в ней не учтены все факторы или если параметры и уравнения модели выбраны неправильно. Это может привести к неверным результатам и неправильным выводам.
5. Ограничение на точность результатов: Все математические модели имеют ограничение на точность результатов. Они могут давать только приближенные ответы, которые могут существенно отличаться от реальных значений. Кроме того, точность модели может зависеть от выбранных параметров и условий моделирования.
6. Сложность интерпретации результатов: Иногда результаты математического моделирования могут быть сложными для интерпретации. Они могут требовать специальных навыков и знаний, чтобы правильно понять их смысл и применить их на практике.
7. Затраты на разработку и обслуживание: Создание и поддержание математических моделей может быть трудоемким и затратным процессом. Необходимо иметь специалистов, занимающихся моделированием, и выделять ресурсы на обновление и поддержку модели.
В целом, математическое моделирование является мощным инструментом для исследования и анализа сложных систем. Однако, оно имеет свои ограничения и недостатки, которые необходимо учитывать при его применении.
Субъективность и приближенность
Кроме того, математическое моделирование всегда основано на данных, которые могут быть приближенными или неточными. В реальных системах существуют много неизвестных и неопределенных факторов, которые могут сильно влиять на результаты моделирования. В таких случаях математическая модель может не давать точных и надежных прогнозов.
Также, при построении математической модели, исследователь может вносить собственные предположения и суждения, что делает модель субъективной. Это значит, что разные исследователи могут создать разные модели для одной и той же системы, что может привести к различным результатам и выводам.
Таким образом, субъективность и приближенность являются важными аспектами математического моделирования, которые необходимо учитывать при анализе и интерпретации результатов моделирования.
Сложность и необходимость вычислений

Иногда математическое моделирование может быть неприменимо из-за слишком большого объема данных или сложности алгоритмов. Например, при моделировании сложных физических процессов или экономических систем может потребоваться огромное количество вычислений, что приводит к высокому времени выполнения и невозможности получения результатов в разумные сроки.
Однако несмотря на сложность вычислений, математическое моделирование остается необходимым инструментом во многих областях. Оно позволяет анализировать и предсказывать поведение систем, улучшать процессы, принимать обоснованные решения и оптимизировать ресурсы.
В некоторых случаях можно использовать приближенные методы и упрощенные модели, которые позволяют получить результаты с достаточной точностью при меньших вычислительных затратах. Тем не менее, при работе с сложными системами все равно может потребоваться использование мощных компьютеров и параллельных вычислений для обработки больших объемов данных и выполнения сложных алгоритмов.
Неучтение факторов окружающей среды
Например, при моделировании климатических изменений могут не учитываться такие факторы, как влияние вулканической активности, аэрозолей в атмосфере, изменения в земной коре и другие. В результате, математическая модель может дать неполную искаженную картину реальных процессов.
Также, при моделировании экологических систем может происходить недооценка влияния различных факторов окружающей среды, таких как загрязнение воздуха, вода или почва, на живые организмы. Из-за сложности учета всех этих взаимодействий, моделирование может не смоделировать полностью все аспекты окружающей среды.
Таким образом, неучтение факторов окружающей среды является серьезным ограничением математического моделирования, которое может привести к некорректным результатам и неполным выводам. Важно понимать, что математическое моделирование является инструментом, который требует аккуратного подхода и учета всех важных факторов окружающей среды для достижения достоверных результатов.
Неопределенность и риски
Кроме того, математическое моделирование не учитывает все возможные риски и несет определенную степень риска. Например, модели могут использовать статистические данные, которые могут быть подвержены ошибкам или искажениям. Также модели могут не учитывать потенциальные изменения в условиях или внешние воздействия, которые могут повлиять на результаты моделирования.
Преимущества математического моделированияНеопределенность и риски
| Позволяет анализировать и прогнозировать сложные системы | Модели основаны на предположениях и упрощениях |
| Позволяет проводить эксперименты в виртуальной среде | Не учитывает все возможные факторы и риски |
| Позволяет оптимизировать решения и принимать обоснованные решения | Могут быть ошибки в статистических данных |
В целом, неопределенность и риски являются неотъемлемой частью математического моделирования. Важно осознавать, что математическая модель не является идеальным отражением реальности и что результаты моделирования могут быть ограничены исходными данными и предположениями, на которых она основана.
Ограниченность применимости

Кроме того, математические модели обычно строятся на основе определенных предположений и упрощений, которые могут не всегда быть верными или точными. Это может приводить к неточным или искаженным результатам моделирования.
Также стоит отметить, что математическое моделирование не всегда может учитывать изменчивость и неопределенность реальной ситуации. Многие явления и процессы могут быть сложными и иметь непредсказуемые результаты, которые невозможно точно отобразить с помощью математических моделей.
Наконец, математическое моделирование требует наличия достаточного объема данных для создания и проверки моделей. В некоторых случаях такие данные могут быть недоступны или не полные, что может привести к неточным результатам или невозможности построения моделей вообще.
В целом, ограниченность применимости математического моделирования означает, что оно не является универсальным инструментом и может быть полезно только в определенных условиях и для решения определенных задач.
Видео по теме:
Вопрос-ответ:
Зачем использовать математическое моделирование?
Математическое моделирование позволяет анализировать и прогнозировать различные явления и процессы, что помогает принимать более обоснованные решения в различных областях, таких как физика, экономика, биология и другие.
Какие преимущества имеет математическое моделирование?
Математическое моделирование позволяет упростить сложные явления и процессы, а также создать систему уравнений, описывающих эти явления. Это позволяет проводить анализ и прогнозирование, тестировать различные сценарии и оптимизировать решения.
Может ли математическое моделирование помочь в разработке новых продуктов?
Да, математическое моделирование может быть полезным инструментом при разработке новых продуктов. С помощью моделирования можно определить оптимальные параметры продукта, провести тестирование различных вариантов и прогнозировать его характеристики.
Какие ограничения есть у математического моделирования?
Одним из ограничений математического моделирования является необходимость упрощения реальных явлений. Модели представляют собой абстракции, которые не всегда могут полностью отражать сложность реального мира. Кроме того, при моделировании нужно учитывать предположения и приближения, которые могут влиять на точность результатов.
Может ли математическое моделирование заменить эксперименты?
Математическое моделирование может быть полезным инструментом для проведения предварительных исследований и оптимизации процессов, но оно не может полностью заменить эксперименты. Реальные эксперименты помогают проверить и подтвердить результаты моделирования, а также учесть факторы, которые не были учтены в модели.
Какие преимущества есть у математического моделирования?
Преимущества математического моделирования включают возможность анализа сложных систем, прогнозирования и оптимизации процессов, упрощение решения сложных задач и повышение эффективности принятия решений.
Зависимость от качества входных данных

Если входные данные содержат ошибки или неточности, то результаты моделирования могут быть неправильными или недостоверными. Несмотря на то, что математические модели могут быть очень точными и детализированными, их результаты становятся бессмысленными, если входные данные неточны или недостоверны.
Поэтому, чтобы получить достоверные результаты, необходимо уделить особое внимание качеству входных данных. Важно проверять их на достоверность, исключать ошибки и неточности. Также необходимо анализировать и учитывать возможные факторы, которые могут влиять на качество данных.
Недостаточное качество входных данных может привести к следующим проблемам:
1. Неверное представление реальности: Если входные данные содержат ошибки или неточности, то результаты моделирования могут не отражать реальность. Это может привести к неверным выводам и неправильным решениям.
2. Недостоверные результаты: Если входные данные содержат ошибки, то результаты моделирования могут быть недостоверными. Это может привести к неправильным прогнозам и плохим решениям.
3. Потеря ресурсов: Если качество входных данных низкое, то время и ресурсы, затраченные на моделирование, могут быть потеряны. Кроме того, неправильные результаты моделирования могут привести к неправильному использованию ресурсов.
В целом, качество входных данных является критическим фактором для успешного математического моделирования. Необходимо уделить должное внимание проверке и улучшению качества данных, чтобы получить достоверные и точные результаты.
Возможность искажения результатов
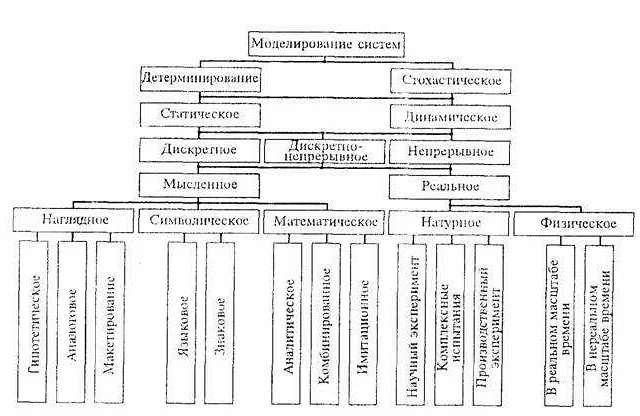
При построении математической модели необходимо учитывать все факторы и взаимосвязи между ними. Однако, в реальности не всегда возможно учесть все аспекты и переменные, которые влияют на изучаемую систему. Это может привести к искажению результатов моделирования и, как следствие, к неверным выводам.
Более того, сам процесс моделирования может быть неполным или некорректным. Неправильное представление входных данных, ошибки в формулировке уравнений или неверные допущения могут привести к искажению результатов и их неправильной интерпретации.
Еще одним фактором, способным искажать результаты моделирования, является человеческий фактор. В процессе работы с математической моделью могут возникать недочеты, ошибки и предубеждения, которые могут повлиять на результаты исследования.
Таким образом, возможность искажения результатов является одним из недостатков математического моделирования. Важно учитывать эти ограничения и применять моделирование с осторожностью, осознавая все его преимущества и ограничения.


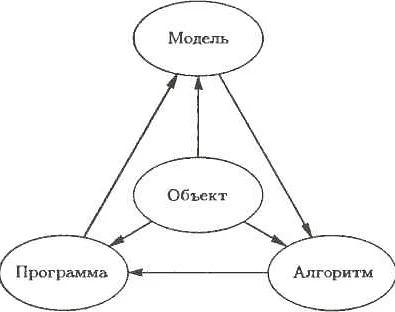

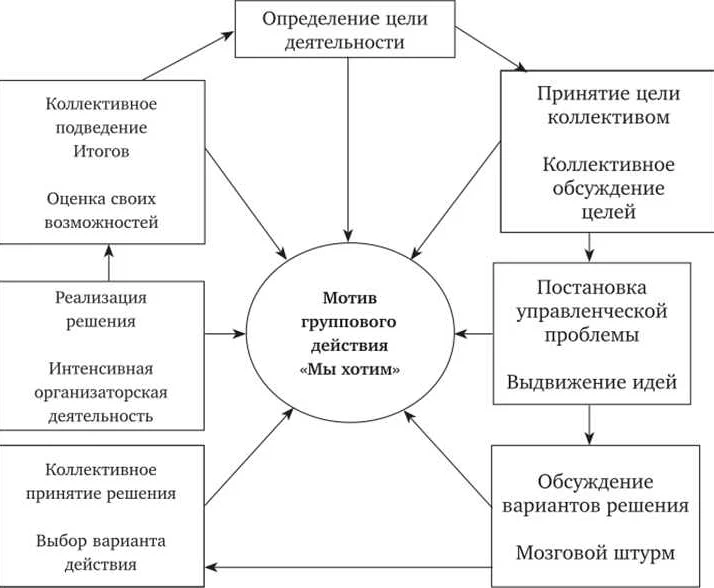
Математическое моделирование является мощным инструментом во многих областях, но не следует забывать и о его ограничениях. Во-первых, математические модели предполагают определенные упрощения реальности, что может привести к потере некоторых деталей и нюансов. Во-вторых, модели могут быть недостаточно точными из-за неполных или неточных данных, что может привести к неверным результатам. Кроме того, моделирующие алгоритмы могут работать в идеальных условиях, которые не всегда соответствуют реальности. Наконец, слишком сложные модели могут быть трудными в интерпретации, что может затруднить принятие правильных решений. Все эти факторы следует учитывать при использовании математического моделирования и не принимать его результаты беспрекословно.
Математическое моделирование весьма полезный инструмент, но не стоит забывать, что у него есть и некоторые ограничения. Одним из основных недостатков является то, что математические модели могут быть слишком упрощенными и не учитывать все факторы, которые могут влиять на реальные процессы. Также, модели могут быть построены на основе предположений, которые могут быть неверными или устаревшими. Еще одним ограничением является необходимость вводить большое количество данных для построения модели, что может быть затратным и трудоемким процессом. Кроме того, математическое моделирование не всегда может учесть человеческий фактор, так как человеческое поведение и решения могут быть сложными и непредсказуемыми. Все эти факторы следует учитывать при использовании математического моделирования и принимать его результаты с определенной осторожностью.
Математическое моделирование является мощным инструментом, который помогает нам понять и предсказывать сложные явления в природе и обществе. Однако, несмотря на все его преимущества, есть и некоторые важные аспекты, которые следует учитывать. Во-первых, математическое моделирование основано на упрощениях и предположениях, которые могут быть не всегда точными или репрезентативными для реальности. Это может привести к неправильным выводам и предсказаниям, особенно если модель слабо соответствует реальной ситуации. Во-вторых, математические модели не могут учесть все факторы, которые влияют на сложные системы. Например, человеческое поведение или случайные события могут оказывать значительное влияние на исследуемый процесс, но они трудно поддаются математическому описанию. Кроме того, математическое моделирование может быть сложным и требовать от пользователя специальных навыков и знаний. Не каждый может использовать эти инструменты эффективно, что может стать преградой для их повседневного использования. Наконец, результаты математического моделирования могут быть ограничены его точностью и надежностью. Даже самая точная модель может давать лишь приближенные результаты, которые нужно интерпретировать с осторожностью. Таким образом, несмотря на все преимущества математического моделирования, следует помнить о его ограничениях и использовать его с умом и осторожностью.
Статья очень интересная и информативная. Она показывает все преимущества математического моделирования, но не стоит забывать, что есть и некоторые недостатки. Например, при создании математической модели мы учитываем только определенные факторы и исключаем все остальные влияния, что может привести к неточным результатам. Также, в математическом моделировании не всегда учитывается человеческий фактор, эмоции и интуиция, которые также играют важную роль. Кроме того, для создания и анализа математических моделей требуется высокий уровень математической подготовки, что ограничивает доступность этого инструмента для многих людей. В целом, математическое моделирование очень полезно и эффективно, но необходимо учитывать и эти недостатки.