Математическое моделирование: ключевой метод научного познания

Математическое моделирование является одним из ключевых методов научного познания, позволяющим создавать абстрактные модели реальных явлений и объектов. В данной статье мы рассмотрим не только основные принципы и методы математического моделирования, но и его применение в различных областях науки и техники.

В различных областях науки и техники математическое моделирование играет ключевую роль при решении задач. Этот метод позволяет нам создавать упрощенные, но все еще реалистичные физические и абстрактные модели, которые можно анализировать и экспериментировать с ними, чтобы предсказать поведение реальных систем в некоторой степени точности. В этой статье мы рассмотрим, что такое математическое моделирование и почему это так важно для научного познания.

Математическое моделирование рассматривается как процесс создания математической модели из реальной системы или процесса. С этой точки зрения модель является абстракцией реальной системы или процесса, которая упрощает его, но все еще сохраняет некоторые из его ключевых аспектов. Математическое моделирование может использоваться во многих областях, таких как физика, биология, экономика, инженерия и многие другие.

Математическое моделирование играет важную роль в научном познании, поскольку оно позволяет нам заменить эмпирический метод анализа реальных систем методом математического анализа. Это означает, что мы можем использовать математические модели для проведения экспериментов над физическими или абстрактными системами в различных условиях.

Определение математического моделирования

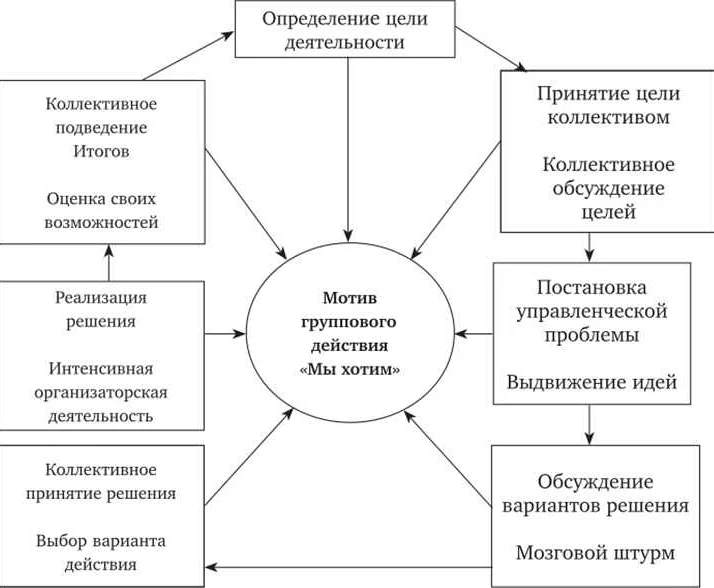
Математическое моделирование — это метод исследования, который заключается в создании математических моделей объектов и процессов реального мира. Математическая модель — это совокупность математических формул и выражений, которые описывают свойства и характеристики изучаемого объекта или процесса. Модель может быть как аналитической, так и численной.

Математическое моделирование используется в разных областях знаний, включая физику, биологию, химию, экономику, социологию, инженерию и другие. Оно позволяет более глубоко понимать реальный мир, а также предсказывать поведение систем при различных условиях и оптимизировать их работу. Поэтому математическое моделирование является неотъемлемой частью современной науки и технологии.

Создание математических моделей может быть сложным и трудоемким процессом, требующим знаний в различных областях математики, физики, программирования и других наук. Однако, оно является мощным инструментом для научного познания реального мира, а также для принятия эффективных решений в различных областях жизни.

Важно отметить, что математическая модель всегда является упрощенным представлением реального мира, и может содержать допущения и ограничения. Поэтому она должна использоваться с осторожностью, и результаты моделирования всегда должны быть проверены экспериментально или сравнены с реальными наблюдениями и данных.

Таким образом, математическое моделирование является мощным и важным методом научного познания, который широко используется в различных областях знаний. Создание математических моделей может быть сложным и трудоемким процессом, но результаты моделирования могут помочь более глубоко понять реальный мир и принимать эффективные решения во многих областях жизни.

Видео по теме:

Цели и принципы математического моделирования

Математическое моделирование является мощным инструментом научного познания и применяется в различных областях знания. Его основная задача — создание моделей, которые полностью или частично описывают наблюдаемую реальность и позволяют предсказывать ее развитие в различных условиях.

Основными целями математического моделирования являются:

• понимание основных закономерностей функционирования системы;
• предсказание результатов действия на систему различных внешних воздействий;
• определение оптимальных решений в различных ситуациях;
• создание условий для управления и контроля за процессом развития системы.

Для достижения этих целей математическое моделирование руководствуется рядом принципов, среди которых можно выделить следующие:

1. Универсальность — модель должна описывать основные закономерности развития системы в различных условиях;
2. Простота — модель должна быть понятной и легко обрабатываемой;
3. Достоверность — результаты моделирования должны быть подтверждены экспериментальными данными;
4. Адекватность — модель должна отражать основные характеристики реальной системы;
5. Масштабируемость — модель должна быть применима для систем различного уровня сложности;
6. Гибкость — модель должна позволять изменять параметры системы и внешние воздействия для определения оптимальных решений в различных ситуациях.

Соблюдение этих принципов позволяет создавать эффективные математические модели, которые находят применение в научных и инженерных исследованиях, планировании мероприятий, оптимизации производственных процессов, прогнозировании различных явлений и процессов и других областях деятельности.

Примеры применения математического моделирования в научных исследованиях

Математическое моделирование является важным инструментом в научных исследованиях. Оно позволяет ученым разрабатывать и тестировать гипотезы без необходимости проводить дорогостоящие эксперименты в реальном мире.

Одним из примеров применения математического моделирования является моделирование погоды. С помощью математических моделей ученые могут предсказать погодные условия на основе данных о температуре воздуха, направлении ветра, влажности и других факторов. Это позволяет людям готовиться к неблагоприятным погодным условиям и принимать меры для минимизации их влияния.

Еще одним примером является применение математического моделирования в физике. Ученые используют математические модели для изучения поведения частиц на уровне атомов и молекул. Это помогает понять физические явления, такие как радиационные пояса Земли или рождение новых звезд.

Математическое моделирование также находит свое применение в медицине. Например, ученые могут создавать модели, чтобы изучать распространение вирусов и бактерий, а также оценивать эффективность различных лечебных методик. Это позволяет ученым более эффективно бороться с заболеваниями и спасать миллионы жизней.

В целом, математическое моделирование имеет широкий спектр применений в научных исследованиях. Оно позволяет ученым лучше понимать мир, который нас окружает, и делать более точные и предсказуемые прогнозы. С развитием технологий математическое моделирование станет еще более важным инструментом для ученых со всего мира.

Вопрос-ответ:

Что такое математическое моделирование?

Математическое моделирование — это метод научного познания, заключающийся в создании моделей объектов данного класса и анализе их поведения для получения новых знаний.

Какими областями науки пользуется математическое моделирование?

Математическое моделирование используется в различных областях науки, таких как физика, экономика, биология, механика и др.

Какими преимуществами обладает математическое моделирование?

Математическое моделирование позволяет анализировать объекты в условиях динамических изменений, проводить эксперименты без реальных затрат и повышает точность получаемых результатов.

Как создается математическая модель?

Создание математической модели зависит от конкретной задачи и объекта, для которого эта модель создается. Обычно модель создается на основе законов физики, химии, биологии и т.д., а также входных данных, на которых эта модель будет тестироваться.

Какие методы математического моделирования существуют?

Существует множество методов математического моделирования, таких как дифференциальные уравнения, вероятностные модели, методы оптимизации, статистические методы и др.

Какие ограничения имеет математическое моделирование?

Математическое моделирование ограничено достоверностью доступных экспериментальных данных, необходимостью учета всех параметров объекта, сложностью и объемом создания моделей.

Какие задачи возможно решить с помощью математического моделирования?

С помощью математического моделирования можно решать задачи прогнозирования, оптимизации, управления и т.д. Например, можно создать модель экономической системы для прогнозирования ее развития или создать модель автоматического управления для оптимизации процесса.

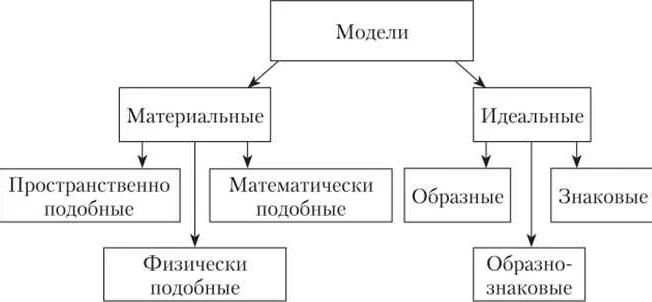
Различные виды математических моделей

Математическое моделирование – это способ представления реальных процессов и систем с помощью математических уравнений или формул. Существует несколько видов математических моделей, которые используются для решения разных задач в различных областях знаний.

• Аналитические модели – это модели, которые описывают систему с помощью аналитических функций, формул и уравнений. Данные модели позволяют получить точные решения и фактически представляют собой законы природы, которые можно использовать для изучения процессов в любой точке пространства и времени.
• Численные модели – это модели, которые основаны на численных методах решения задач. Они используются для решения задач, которые не имеют аналитического решения, или когда аналитическое решение слишком сложно или невозможно получить за разумное время.
• Стохастические модели – это модели, которые учитывают случайные факторы и вероятностный характер процессов. Они используются для изучения систем, которые не могут быть описаны точными математическими уравнениями и имеют большую степень неопределенности.
• Эмпирические модели – это модели, которые основаны на экспериментальных данных и наблюдениях. Они используются для изучения систем, для которых нет научного объяснения или теоретической базы, и для которых экспериментальные данные являются единственным источником информации.
• Имитационные модели – это модели, которые создаются для подражания реальным системам и процессам. Они позволяют проводить эксперименты в виртуальной среде, что может быть полезно, например, для изучения сложных экономических систем или моделирования экологических катастроф.

Различные виды математических моделей имеют свои преимущества и ограничения, и выбор определенной модели зависит от конкретной задачи и условий ее решения.

Математические модели в экономике и финансах

Экономика и финансы — сферы, где математика и математическое моделирование играют важную роль. Модель — это абстрактная математическая структура, описывающая совокупность эффектов и влияний для исследования или прогнозирования явлений, составляющих объект изучения.

Математические модели экономики и финансов используются для анализа различных экономических и финансовых процессов, таких как рынки ценных бумаг, банковские операции, инфляция, налоги и другие. Они позволяют прогнозировать будущее поведение этих процессов и принимать решения на основе этих прогнозов.

Одним из примеров применения математических моделей в экономике и финансах является оценка рисков на финансовых рынках. Моделирование рисков позволяет выявлять возможные потери, оценивать вероятность этих потерь и разрабатывать стратегии управления рисками.

Еще один пример — это моделирование рыночных цен на товары и услуги. Математические модели позволяют анализировать рыночное поведение потребителей и производителей, оценивать цены и объемы производства, а также определять налоговую политику и другие экономические инструменты.

В заключение стоит отметить, что математические модели в экономике и финансах не являются универсальным решением, их результаты не могут считаться абсолютными. Однако, они помогают установить связи между различными явлениями, а также представляют собой ценный инструмент для принятия важных решений в экономических и финансовых сферах.

Математические модели в биологии и медицине

Использование математических моделей в биологии и медицине позволяет исследовать сложные процессы, которые не могут быть полностью выявлены с помощью обычных экспериментов. Моделирование позволяет предсказывать результаты воздействия различных факторов на биологические системы, что позволяет лучше понимать причины различных заболеваний и поисковые методы их лечения.

В биологии, математические модели используются, например, для исследования динамики популяций, развития опухолевых клеток, механизмов передачи генетической информации и других процессов. Важным преимуществом моделирования является возможность исследовать эти процессы в контролируемых условиях, что часто невозможно в реальных экспериментах.

В медицине, математические модели широко используются для изучения болезней и их лечения. Такие модели могут помочь определить, как действует лекарство на уровне организма, каким образом оно влияет на метаболические процессы и какова будет динамика заболевания при лечении различными методами.

Таким образом, математические модели в биологии и медицине являются мощным инструментом для исследования и предсказания биологических процессов. Их использование помогает разрабатывать новые методы диагностики и лечения заболеваний, что позволяет улучшить качество жизни людей.

Математические модели в физике и инженерии

Математические модели играют огромную роль в физике и инженерии. Они позволяют описывать и предсказывать поведение различных систем и явлений, а также совершенствовать существующие технологии.

В физике математические модели помогают исследовать различные явления в природе, такие как движение тел, распространение света, взаимодействие частиц и многое другое. Благодаря математическим моделям ученые могут предсказывать поведение систем в различных условиях и создавать новые материалы и технологии.

В инженерии математические модели позволяют создавать более эффективные и надежные системы. Инженеры используют математические модели для проектирования различных конструкций, например, зданий, мостов, летательных аппаратов и транспортных средств. Это помогает им улучшать характеристики систем и повышать их безопасность и эффективность.

• Математические модели в физике и инженерии:
• Позволяют описывать и предсказывать поведение систем и явлений;
• Помогают создавать новые материалы и технологии;
• Позволяют создавать более эффективные и надежные системы.

Эмпирический и теоретический анализ математических моделей

Математическое моделирование – это процесс создания математических моделей для анализа и понимания реальных процессов и явлений. Эти модели могут быть использованы для прогнозирования будущих событий, определения оптимальных стратегий и принятия решений в различных сферах, от науки до бизнеса.

Одной из важных задач при создании математических моделей является оценка их точности и надежности. Точность модели может быть проверена экспериментально, путем ее эмпирического анализа. Такой анализ позволяет сравнить реальные данные с результатами, полученными при использовании модели. Если модель дает точные предсказания, это говорит о ее качестве и полезности.

Также важен теоретический анализ модели. Он заключается в изучении математических свойств модели и ее поведения в различных условиях. Теоретический анализ позволяет исследователям понять, какие аспекты модели являются наиболее важными, а какие могут быть опущены без ущерба для ее точности. Кроме того, он может помочь определить пределы применимости модели и выявить ее ограничения.

Эмпирический и теоретический анализ являются важными компонентами математического моделирования. Они позволяют достичь максимальной точности и надежности модели, что является необходимым для ее успешного использования в практике.

Оценка точности математических моделей

Одной из ключевых задач математического моделирования является оценка точности созданных моделей. Это задача не менее важна, чем само создание моделей и позволяет определить их пригодность для практического применения.

Для оценки точности математических моделей применяют различные методы, такие как проверка модели на экспериментальных данных, анализ погрешностей, сравнение результатов, полученных разными методами и т.д.

Одним из наиболее распространенных методов оценки точности является метод наименьших квадратов. Он позволяет построить график, на котором модельные значения сравниваются с фактическими данными и определяется степень соответствия модели реальным данным. Например, данная методика может быть применена для оценки качества моделирования тока в цепи электрической цепи.

Кроме того, для оценки точности моделей часто используется метод перекрестной проверки. Он позволяет оценить работоспособность модели на отложенных данных и проверить ее на способность обобщения. Такой подход часто используют при моделировании финансовых рынков, где очень важно получать точные прогнозы.

В любом случае, важно помнить, что оценка точности математических моделей является сложным и многоэтапным процессом, требующим как теоретических знаний, так и практического опыта.

Преимущества и недостатки математических моделей

Математическая модель является одним из наиболее мощных инструментов науки и техники. Моделирование позволяет прогнозировать будущее поведение объектов, анализировать их свойства и изучать различные варианты развития событий. Однако, как и любой метод, математические модели имеют свои преимущества и недостатки.

Преимущества математических моделей:

• Возможность точного и количественного описания процессов;
• Экономия времени и средств, которые необходимы для проведения экспериментов в реальных условиях;
• Возможность изучения объектов и процессов, которые невозможно или трудно изучить в реальных условиях (например, астрономические объекты);
• Возможность определения оптимальных параметров объектов и процессов, что позволяет экономить средства и энергию;
• Возможность создания прототипов и разработки новых технологий без непосредственного их создания в реальных условиях.

Недостатки математических моделей:

• Невозможность включения в модель всех возможных факторов и переменных, влияющих на объект и процесс;
• Ошибки и неточности входных данных, которые могут привести к неправильным результатам;
• Необходимость представления объекта или процесса в упрощенной форме, что может существенно исказить реальную картину поведения;
• Невозможность учесть возможные события, которые не имели места в прошлом, но могут произойти в будущем.

Тем не менее, несмотря на эти недостатки, математические модели продолжат играть важную роль в науке и технике, помогая исследователям получать новые знания и разрабатывать новые технологии.