Что не относится к математическим способам и приемам анализа

Математический анализ исключает из своего спектра несколько методов и приемов, таких как эмоциональная или интуитивная оценка, субъективное мнение и предположения, не подкрепленные доказательствами. В данной статье рассматриваются методы, не применимые в математическом анализе.

Математический анализ – это раздел математики, который изучает пределы, производные, интегралы и ряды. Он является основой для многих других математических дисциплин и науки в целом. Однако, есть несколько важных вещей, которые не включаются в математический анализ, хотя они могут казаться связанными с ним.

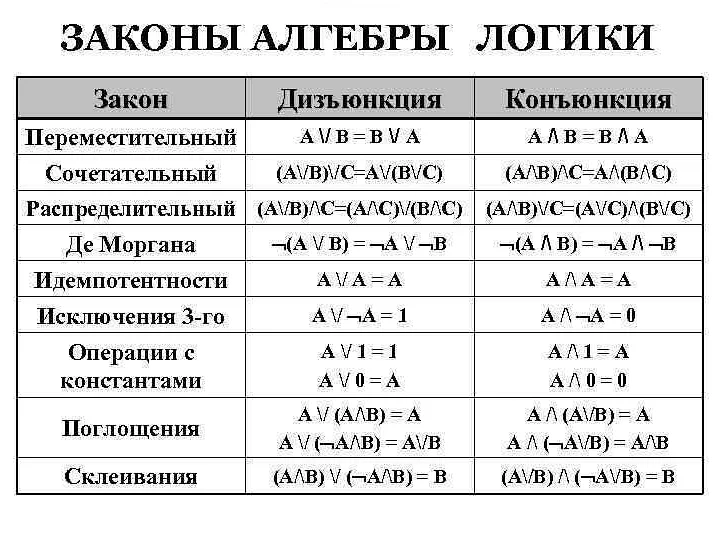
Во-первых, математический анализ не включает в себя формальную логику. Хотя логика является фундаментальной частью математики, она имеет свои собственные принципы и методы. Формальная логика изучает правила рассуждения и доказательства, которые используются в математике, но она не относится непосредственно к анализу функций и их свойств.

Во-вторых, математический анализ не включает в себя алгебру. Алгебра изучает структуры и операции, такие как уравнения, группы, поля и кольца. Она имеет свои собственные методы и теоремы, которые не всегда применимы в контексте математического анализа. Хотя алгебра и является тесно связанной с анализом, они представляют разные аспекты математики.

Математический анализ – это мощный инструмент для понимания и анализа функций и их свойств. Он помогает решать сложные проблемы в различных областях науки и техники. Однако, как и в любой науке, есть границы того, что включается и не включается в область математического анализа. Понимание этих границ поможет более глубоко и точно применять методы анализа и дополнить его другими математическими инструментами.

Математический анализ: что исключено из области исследования

Во-первых, математический анализ не занимается изучением конкретных функций. Вместо этого, он фокусируется на анализе общих свойств функций и разработке общих методов решения задач. Он не затрагивает специфические свойства, например, графиков функций или их поведения в конкретных точках.

Во-вторых, математический анализ не исследует геометрические свойства фигур и пространств. Такие вопросы, как форма фигур, их площадь, объем или границы, относятся к другим областям математики, таким как геометрия или топология.

Кроме того, математический анализ не занимается изучением дискретных структур и дискретных математических объектов. Он направлен на анализ непрерывных функций и непрерывных математических объектов. Дискретные системы, такие как графы, алгоритмы или теория чисел, изучаются в других областях математики.

ТемаВключено в математический анализ?

Изучение конкретных функций	Нет
Геометрические свойства фигур и пространств	Нет
Дискретные структуры и объекты	Нет

Таким образом, математический анализ является мощным инструментом для изучения общих свойств функций и математических объектов, но он не включает в себя изучение конкретных функций, геометрических свойств и дискретных структур.

История развития математического анализа

История математического анализа начинается со времен Древней Греции, где первые идеи этой дисциплины были предложены прославленным математиком Архимедом. В его работе «Методы» он разработал принципы и методы, которые впоследствии стали основой математического анализа.

Однако, настоящее развитие математического анализа произошло в эпоху Просвещения в XVII-XVIII веках. Великие математики того времени, такие как Исаак Ньютон и Готфрид Лейбниц, внесли огромный вклад в развитие аналитической геометрии и дифференциального исчисления.

В XIX веке математический анализ стал еще более развитым и широко применяемым. Великие математики того времени, включая Леонарда Эйлера, Карла Фридриха Гаусса и Августа Коши, дополнили и усовершенствовали теорию математического анализа.

В XX веке математический анализ продолжил свое развитие, и появились новые направления, такие как функциональный анализ и теория меры. Современный математический анализ является основой для многих других математических дисциплин и имеет широкое применение в физике, экономике, компьютерных науках и других областях знания.

Таким образом, история развития математического анализа свидетельствует о его важности и значимости в математике и других наук.

Понятие исчисления пределов

Предел функции является центральным понятием исчисления пределов. Он определяется как значение, к которому функция стремится, когда ее аргумент приближается к определенной точке. Предел может быть конечным или бесконечным, положительным или отрицательным.

Исчисление пределов также включает понятие бесконечно малых и бесконечно больших величин. Бесконечно малая величина — это такая функция, которая стремится к нулю при приближении аргумента к некоторой точке. Бесконечно большая величина, наоборот, стремится к бесконечности при приближении аргумента к некоторой точке.

В исчислении пределов также рассматриваются понятия непрерывности функций и их производных. Непрерывность функции означает, что ее значения изменяются плавно и без разрывов в заданной области. Производная функции показывает скорость ее изменения в каждой точке области.

Исчисление пределов имеет широкое применение в различных областях математики, физики, экономики и других наук. Оно позволяет анализировать и предсказывать поведение функций и их свойства на основе их пределов и производных.

Примеры использования исчисления пределов:

— Определение скорости изменения параметров в физических процессах

— Оптимизация функций и поиск экстремумов

— Анализ поведения функций в математической моделировании

— Разработка алгоритмов численных методов решения уравнений

Алгебраический анализ

В алгебраическом анализе исследуются свойства и структуры алгебраических объектов, а также операции, которые можно выполнять с этими объектами. Это включает в себя изучение симметрии, групповых законов, преобразований, сопряженных классов и многое другое.

Алгебраический анализ находит применение во многих областях, включая теорию чисел, криптографию, компьютерную науку, физику и химию. Он помогает в понимании и решении сложных задач, связанных с алгебраическими структурами и их свойствами.

В общем, алгебраический анализ является важным инструментом для изучения алгебраических систем и развития абстрактного мышления. Он предлагает математический фреймворк для понимания и решения различных проблем, связанных с алгебраическими объектами и их взаимодействием.

Дифференциальное исчисление

Основной инструмент дифференциального исчисления — производная функции. Производная функции показывает, как быстро меняется значение функции в каждой точке ее области определения. Она играет ключевую роль в решении различных задач, таких как нахождение экстремумов функций, изучение поведения функций на интервалах, и многое другое.

Важными понятиями, связанными с дифференциальным исчислением, являются точка экстремума, точка перегиба, асимптоты и т.д. На основе производной функции можно определить, в каких точках функция достигает экстремальных значений, имеет точки перегиба или асимптоты. Эти понятия играют важную роль в анализе функций и их графиков.

Одной из основных теорем дифференциального исчисления является теорема Ферма, которая утверждает, что если функция имеет экстремум внутри своей области определения, то производная функции в этой точке равна нулю. Это позволяет находить точки экстремума функций путем решения уравнения на производную.

Таким образом, дифференциальное исчисление играет важную роль в математическом анализе, позволяя анализировать и изучать свойства функций в малом масштабе. Оно является основой для решения различных задач и нахождения экстремальных значений функций.

Интегральное исчисление

Интегралы позволяют находить площади под графиками функций, вычислять средние значения функций, находить массу тела или объем жидкости по плотности и другие приложения в различных областях науки и инженерии.

Основными понятиями в интегральном исчислении являются определенный и неопределенный интегралы. Неопределенный интеграл — это функция, обратная производной. Он позволяет находить не только значение функции, но и ее первообразную. Определенный интеграл — это число, являющееся результатом вычисления определенного интеграла.

Интегральное исчисление также включает в себя различные методы вычисления интегралов, такие как метод замены переменной, интегрирование по частям и разложение на простейшие дроби.

ОпределениеОбозначение

Определенный интеграл	∫ab f(x) dx
Неопределенный интеграл	∫ f(x) dx
Метод замены переменной	u = g(x)
Интегрирование по частям	∫ u dv = uv — ∫ v du
Разложение на простейшие дроби	f(x) = ½∫A g(x) dx + ½∫B h(x) dx

Теория рядов

Теория рядов изучает свойства и поведение рядов, которые представляют собой бесконечные суммы элементов. Ряды могут быть сходящимися или расходящимися, и теория рядов помогает определить, какой тип ряда имеется.

Основные понятия, изучаемые в теории рядов, включают понятия сходимости и расходимости ряда, суммы ряда, а также критерии сходимости, такие как критерий Коши и критерий Даламбера. Также изучаются операции над рядами, такие как суммирование и умножение рядов.

Теория рядов находит применение во многих областях математики и физики. Например, ряды используются для разложения функций в ряды Тейлора или ряды Фурье, что позволяет приближенно описывать сложные функции с помощью более простых.

Однако стоит отметить, что теория рядов не охватывает другие аспекты математического анализа, такие как дифференциальное и интегральное исчисление. Эти области изучают различные свойства функций и их производных или интегралов, и они имеют свои собственные теоремы и методы.

Видео по теме:

Вопрос-ответ:

Что такое математический анализ?

Математический анализ — это раздел математики, изучающий предельные значения, производные и интегралы функций.

Какие методы используются в математическом анализе?

В математическом анализе используются различные методы и инструменты, такие как пределы, производные, интегралы, ряды, дифференциальные уравнения и другие.

Какие области не включает в себя математический анализ?

Математический анализ не включает в себя такие области, как теория вероятностей, теория игр, математическая логика и дискретная математика.

В чем отличие математического анализа от других математических дисциплин?

Математический анализ отличается от других математических дисциплин тем, что он фокусируется на изучении предельных значений, производных и интегралов функций, в то время как другие дисциплины могут заниматься другими аспектами математики, такими как алгебра, геометрия или теория чисел.

Какую практическую пользу можно получить из изучения математического анализа?

Изучение математического анализа может быть полезным для решения различных проблем и задач, в том числе в физике, экономике, инженерии и других науках. Он также может помочь развить аналитическое мышление и способность к решению сложных задач.

В чем основное отличие математического анализа от алгебры?

Основное отличие математического анализа от алгебры заключается в том, что математический анализ изучает непрерывные и дифференцируемые функции, а также решает задачи, связанные с пределами, производными и интегралами. В отличие от алгебры, которая занимается структурами, операциями и уравнениями, математический анализ углубляется в аспекты непрерывности и дифференцируемости функций.

Многомерный анализ

В многомерном анализе изучаются такие понятия, как частные производные, градиент, дивергенция и ротор, интегралы по поверхностям и объемам, линейные и квадратичные формы, криволинейные интегралы и другие важные математические концепции.

Многомерный анализ имеет широкие применения в различных областях, таких как физика, экономика, инженерия и компьютерная графика. Он позволяет исследовать сложные системы и моделировать их поведение, а также решать задачи оптимизации и управления.

Изучение многомерного анализа требует глубокого понимания математических концепций и навыков работы с многомерными функциями. Эта область математического анализа является основой для более сложных областей, таких как дифференциальные уравнения, теория вероятностей и математическая статистика.

Применение математического анализа в других областях науки

Физика использует математический анализ для описания и объяснения физических явлений. Например, в классической механике математический анализ позволяет решать уравнения движения и определять траектории тел. В теории поля математический анализ используется для описания электромагнитных полей и других физических величин.

Математический анализ также находит применение в экономике. Экономические модели и теории часто основаны на математическом анализе. Например, для определения оптимальных стратегий инвестирования или прогнозирования экономического развития используются математические методы и модели.

Биология и медицина также используют математический анализ для моделирования и анализа биологических систем. Например, математический анализ позволяет описывать динамику популяций, моделировать эволюцию и исследовать болезни с помощью математических моделей.

Космология и астрофизика являются другими областями, где математический анализ находит применение. Математические методы используются для моделирования и анализа гравитационных полей, описания движения планет и звезд, прогнозирования космических явлений.

Таким образом, математический анализ играет важную роль во многих областях науки, помогая описывать и анализировать сложные явления и процессы.