Применение математической логики в науке, технике и повседневной жизни: где она находит применение
Содержимое
- 1 Применение математической логики в науке, технике и повседневной жизни: где она находит применение
- 1.1 Математическая логика в науке и технологиях
- 1.2 Определение математической логики
- 1.3 История развития математической логики
- 1.4 Классическая логика
- 1.5 Модальная логика
- 1.6 Интуиционистская логика
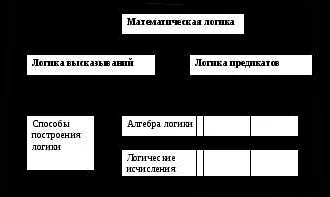
- 1.7 Логика высказываний и логика предикатов
- 1.8 Приложения математической логики в информатике
- 1.9 Применения математической логики в искусственном интеллекте
- 1.10 Математическая логика и теория множеств
- 1.11 Математическая логика и философия
- 1.12 Вопрос-ответ:
- 1.12.0.1 Какие области науки и технологий используют математическую логику?
- 1.12.0.2 Как математическая логика помогает в разработке компьютерных программ?
- 1.12.0.3 Как математическая логика используется в искусственном интеллекте?
- 1.12.0.4 Как математическая логика помогает в криптографии?
- 1.12.0.5 Как математическая логика помогает в автоматическом доказательстве теорем?
- 1.12.0.6 Как математическая логика используется в теории игр?
- 1.12.0.7 Как математическая логика помогает в теории множеств?
- 1.13 Практические применения математической логики в экономике и юриспруденции
- 1.14 Видео по теме:
Математическая логика используется в различных областях, включая информатику, философию, право, экономику, биологию и другие. Она помогает формализовать и обрабатывать знания, а также решать задачи, требующие точности и логического мышления.
Математическая логика – это важная область математики, которая занимается изучением формальных систем и их свойств. Ее различные концепции и техники применяются в разных областях науки и технологий. Она используется для формального моделирования, предсказывания и управления реальными системами, такими как компьютерные сети и программные продукты, а также для изучения последствий принимаемых решений и обоснования новых знаний.
Математическая логика имеет фундаментальное значение в математике, логике, философии и когнитивных науках. Ее инструменты используются для доказательства теорем, решения задач, построения решений. Она играет ключевую роль в математическом моделировании и статистическом анализе данных. Активно применяется и в программировании, где используется для создания логических и последовательных блоков кода, что делает его проще поддерживать, тестировать и обновлять.
Таким образом, математическая логика – важная и актуальная область, которая находит свое применение во многих сферах науки и технологий. Ее изучение и применение могут привести к новым открытиям и решениям разнообразных задач, что сделает нашу жизнь более комфортной и безопасной.
Математическая логика в науке и технологиях
Математическая логика — это область математики, которая изучает формальную логику и различные системы символов и высказываний. Эта область находит широкое применение в науке и технологиях благодаря своей способности строго формализовывать мысли и изложения.
В информатике и технологиях математическая логика играет важную роль в разработке и верификации программного обеспечения. В частности, математическая логика позволяет создавать формальные спецификации программных продуктов, что повышает их качество и надежность. Кроме того, использование математической логики исключает возможность появления ошибок, связанных с неточностями и расхождениями в толковании и формулировке задач.
В науке тоже используют математическую логику для формализации исследований, что позволяет делать выводы на основе четких и точных данных и устанавливать закономерности в сложных процессах. Особенно активное применение математической логики находит в философии, математике, лингвистике и искусственном интеллекте.
Таким образом, математическая логика является неотъемлемой частью современной науки и технологий. Её применение позволяет повышать качество и точность работы программного обеспечения, приближать науку к другим областям знаний и делает современные технологии более надежными и эффективными.
Определение математической логики

Математическая логика — это область математики, которая изучает формальные системы символов и их модели. Она используется для анализа и решения логических задач, таких как доказательство теорем, описание алгоритмов и решение проблем в вычислительной технике.
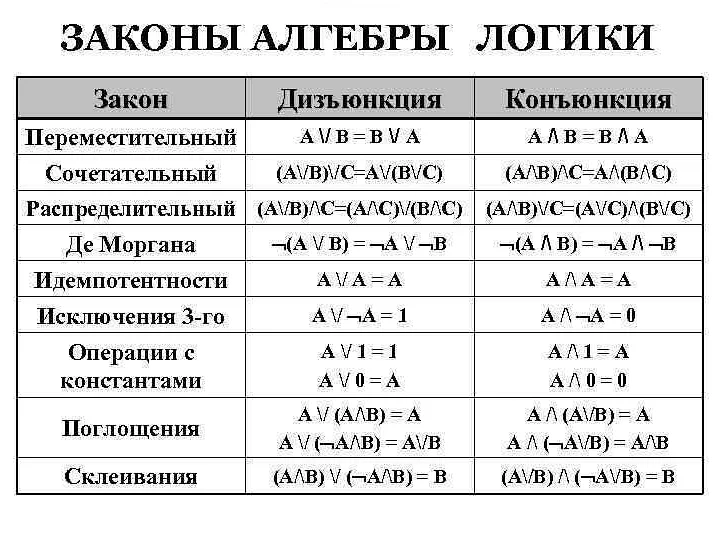
Математическая логика состоит из нескольких разделов, включая символьную логику, теорию множеств, теорию вычислимости и модальную логику. Каждый из этих разделов имеет свои собственные приложения и применения в науке и технологиях.
Символьная логика, например, используется для формализации высказываний и аргументов, что позволяет упростить их анализ и обработку. Теория множеств применяется в математике и физике для определения и описания объектов и их свойств. Модальная логика используется в искусственном интеллекте и философии, чтобы формализовать понятия времени, пространства и знания.
Математическая логика имеет широкие применения в науке и технологиях, а также в других областях, таких как философия, этика и право. Применение математической логики позволяет формализовать и анализировать сложные концепции и принимать обоснованные решения на основе четкой логики и рационального рассуждения.
История развития математической логики
Математическая логика является разделом математики, занимающимся формальным изучением логических систем. Она имеет довольно длинную и интересную историю развития.
Первые шаги в развитии математической логики были сделаны в древней Греции. Аристотель, один из наиболее известных древних греческих философов, в своих трудах заложил основы силлогистики — науки, изучающей формы логических рассуждений.
В средние века философы и ученые прибегали к использованию схоластической логики, которая была основана на трудах Аристотеля. Однако, эта логика была недостаточно развитой и формальной. Настоящая революция в математической логике началась в XIX веке, когда математики начали переносить математическую точность на изучение логических систем.
Большой вклад в развитие математической логики внесли многие известные ученые и математики, такие как Бертран Рассел, Альфред Тарский, Курт Гедель и многие другие. Вместе с ними были разработаны такие понятия, как множества, алгебраическая логика и разные виды математических вычислений.
Сегодня математическая логика является незаменимой частью многих научных и технических областей и используется для формального доказательства теорем, разработки компьютерных алгоритмов, исследований и многого другого.
Классическая логика
Классическая логика является одним из основных направлений математической логики. Эта логика была разработана в древней Греции и описывает утверждения, которые могут быть либо истинными, либо ложными. Классическая логика используется во многих научных и технических областях, в том числе в математике, информатике, философии, праве и других областях.
В классической логике есть несколько основных правил, которые определяют, как она работает. Один из таких правил — закон исключённого третьего. Он гласит, что любое утверждение либо истинно, либо ложно. Другой важный закон — закон противоречия — утверждает, что нельзя одновременно утверждать и отрицать одно и то же утверждение.
Классическая логика часто используется в математике, чтобы формально доказать теоремы и свойства. Например, теорема Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, доказывается классической логикой.
Классическая логика также имеет практические применения, в том числе в области компьютерных наук. Компьютерные программы часто используют условные операторы, чтобы принимать решения на основе логических выражений. Например, программа может проверять, является ли число четным или нечетным, и на основе этого принимать решения о следующих шагах.
Модальная логика
Модальная логика – это раздел математической логики, который изучает логические отношения между различными видами высказываний. В модальной логике используется понятие «модальности», которое относится к тому, какое отношение описывает высказывание: необходимость, возможность, допустимость и т.д.
Модальная логика в научных и технологических областях используется для изучения формализованных систем знаний, рассмотрения логических свойств алгоритмов и управляющих программ, а также проектирования и верификации программного обеспечения.
Одной из областей, в которых применяется модальная логика, является искусственный интеллект. В частности, она используется для формализации высказываний об отношениях и свойствах объектов в мире.
Модальная логика также имеет применение в теории игр, где используется для анализа рациональных стратегий и принятия решений в условиях неопределенности.
Изучение модальной логики помогает лучше понимать многие аспекты, связанные с применением логики в реальных ситуациях, и позволяет разрабатывать более эффективные алгоритмы и технологии в различных областях науки и техники.
Интуиционистская логика
Интуиционистская логика – это логика, принимающая основой не законы классической логики, а принципы интуиционистской математики. Она была создана в начале XX века математиком Л. Бруером и философом И. Бейном. Ограничения классической логики в многом были связаны с ограниченностью формализаций, применявшихся на тот момент. Интуиционистские принципы дают возможность приблизить логику к интуитивной, непосредственной разумности.
Особым образом интуиционистская логика обращается с понятиями, связанными с кванторами всеобщности и существования. Так, в интуиционистской логике формализуется не «все лица смертны», а «у каждого личности есть своя смерть». Следует также отметить, что интуиционистская логика подвергается критике со стороны сторонников конструктивизма в математике: она ограничена и не способна описать все теории и высказывания, которые могут быть описаны классической логикой.
Интуиционистская логика нашла широкое применение в различных областях науки и технологий, в частности, в информатике. Она используется в задачах программирования, при проектировании информационных систем, в теории вычислительных процессов. В интуиционистской логике получили свое развитие и некоторые философские концепции, в частности, теория конструктивистского познания.
- Преимущества интуиционистской логики:
- Приближение логики к непосредственному разумению.
- Контроль открытости и замкнутости систем в контексте выражения теорем.
- Возможность формализации процесса исследования задач.
- Недостатки интуиционистской логики:
- Не способна описать все теории и высказывания, которые могут быть описаны классической логикой.
- Сложность использования в некоторых предметных областях науки.
Логика высказываний и логика предикатов
Логика высказываний и логика предикатов — две основные ветви математической логики. Логика высказываний изучает логические связи между высказываниями, которые могут быть истинными или ложными, но не содержат переменных. В то же время логика предикатов изучает логические связи между высказываниями, содержащими переменные и кванторы.
Область применения логики высказываний включает в себя такие области науки, как математика, информатика, философия, лингвистика и физика. Примеры применения логики высказываний в математике включают в себя доказательство теорем, а в информатике — программирование и разработку алгоритмов.
Логика предикатов охватывает такие области, как математика, информатика, философия, лингвистика, физика и биология. Логика предикатов используется в математических теориях, часто используется в компьютерных программах, например, в программировании баз данных. А в биологии, логика предикатов используется для описания биологических процессов и конструирования искусственных систем.
Таким образом, логика высказываний и логика предикатов, хотя и имеют отличия, являются важными ветвями математической логики и имеют широкий диапазон применений в науке и технологиях.
Приложения математической логики в информатике
Математическая логика является одним из ключевых элементов в области информатики. Она применяется для формализации и описания различных аспектов вычислительных систем.
Одно из основных применений математической логики в информатике — это создание логических схем. Они используются для проектирования систем с заданным поведением, применяются в цифровой электронике для создания блоков управления и функциональных единиц, а также для проектирования баз данных и алгоритмов.
Еще одно приложение математической логики в информатике – это теория алгоритмов, которая является частью теории вычислительных процессов. Она описывает, каким образом можно решить множество задач с помощью вычислительных методов.
Также математическая логика используется в различных областях искусственного интеллекта, например, для создания экспертных систем и систем обработки знаний. Она также находит применение в криптографии, где используется для создания алгоритмов шифрования и расшифровки.
Важно отметить, что математическая логика обеспечивает формальную точность и ясность в описании вычислительных систем, что очень важно при создании сложных программных продуктов, систем автоматического управления и других решений, связанных с обработкой информации.
Итак, можно сказать, что математическая логика является не только теоретической дисциплиной, но и применяемой на практике. Она обеспечивает формализацию и ясность в описании различных аспектов вычислительных систем, что позволяет создавать более эффективные и точные решения в области информатики.
Применения математической логики в искусственном интеллекте
Искусственный интеллект является одним из важнейших применений математической логики. Математические модели, основанные на логических методах, используются для создания компьютерных систем, способных проводить логические выводы и решать задачи, требующие анализа большого объема информации.
Одним из примеров применения логических методов в искусственном интеллекте является система экспертных систем. Эти системы используют базы знаний, содержащие знания и определения в определенной области, и ставят задачи на основе этой информации с использованием логических алгоритмов.
Другими примерами применения математической логики в искусственном интеллекте являются нейронные сети и генетические алгоритмы. Нейронные сети основаны на решении математических задач, а генетические алгоритмы используют логические алгоритмы для создания оптимальных решений задач.
Математическая логика является фундаментальным инструментом для создания и расширения возможностей искусственного интеллекта. Создание эффективных и инновационных систем искусственного интеллекта невозможно без использования математической логики и других методов математического анализа.
Математическая логика и теория множеств

Математическая логика и теория множеств являются двумя основными областями математики, которые находят широкое применение в науке и технологиях.
В математической логике изучаются формальные языки и методы доказательства теорем. Это позволяет разрабатывать алгоритмы решения задач и создавать компьютерные программы, которые используются в разных областях науки и техники.
Теория множеств, в свою очередь, изучает свойства множеств и операции над ними. Она является основой для различных областей математики, таких как теория графов, анализ и топология.
В информатике математическая логика и теория множеств используются для формализации знаний и создания баз данных. Они также находят применение в искусственном интеллекте и теории вычислительных моделей.
В заключение, математическая логика и теория множеств являются неотъемлемыми частями современной науки и технологий, которые позволяют формализовать знания и создать точные алгоритмы для решения различных задач.
Математическая логика и философия

Математическая логика изначально была важным инструментом в философии, позволяющим формализовывать и анализировать различные системы и теории. Философы использовали математическую логику для изучения основных концепций, таких как истина, ложь, вывод и причинность, и для создания формальных доказательств, позволяющих подтверждать или опровергать их теории.
В современной философии математическая логика играет важную роль в анализе широкого круга проблем, таких как этика, онтология, метафизика и философия науки. Она также является важным инструментом для изучения логических структур и определения понятий в различных областях философии.
Одной из наиболее важных областей применения математической логики в философии является теория аргументации. Она используется для определения формальных правил, чтобы определить, какие аргументы являются логически допустимыми и какие — нет. Таким образом, математическая логика позволяет философам уточнить, какие аргументы являются обоснованными, а какие могут быть отвергнуты.
В целом, математическая логика привнесла новые методы и подходы к философии, позволяя создать более строгие и точные теории и аргументы. Она продолжает быть важным инструментом для изучения различных проблем, с которыми сталкиваются философы и ученые в настоящее время.
Вопрос-ответ:
Какие области науки и технологий используют математическую логику?
Математическая логика применяется во многих областях науки и технологий, например, в компьютерных науках, искусственном интеллекте, теории игр, криптографии, автоматическом доказательстве теорем, теории множеств и т.д.
Как математическая логика помогает в разработке компьютерных программ?
Математическая логика используется для формализации и описания правил и алгоритмов, которые компьютер должен выполнить. Она способствует созданию формальной спецификации программного обеспечения, что ускоряет процесс разработки и улучшает качество программ.
Как математическая логика используется в искусственном интеллекте?
Математическая логика используется для создания и описания логических систем, которые могут использоваться для решения задач и принятия решений в различных областях искусственного интеллекта, например, в робототехнике, экспертных системах, компьютерном зрении и машинном обучении.
Как математическая логика помогает в криптографии?
Математическая логика используется для разработки и анализа криптографических методов и протоколов. Она способствует созданию надежных систем защиты данных, которые могут быть использованы для шифрования и расшифровки конфиденциальной информации.
Как математическая логика помогает в автоматическом доказательстве теорем?
Математическая логика используется для создания формализованных математических систем, которые позволяют автоматически доказывать теоремы. Это упрощает процесс написания доказательств и позволяет найти более эффективные решения математических проблем.
Как математическая логика используется в теории игр?
Математическая логика используется для анализа игровых стратегий и поиска оптимальных решений в играх. Это позволяет разработать более эффективные стратегии для игроков и создать более интересные игры.
Как математическая логика помогает в теории множеств?
Математическая логика используется для формализации и описания множеств и операций над ними, что позволяет создать строгое математическое определение множества и рассмотреть его свойства. Это способствует развитию математики и созданию новых математических теорий и концепций.
Практические применения математической логики в экономике и юриспруденции

Математическая логика — это наука, которая позволяет расчленять и анализировать сложные концепте с помощью математических методов. Это нередко используется в таких областях, как экономика и юриспруденция. Математическая логика используется для разработки правил и моделей, которые могут помочь в принятии управленческих и правовых решений.
В экономике математическая логика используется для анализа сложных данных и принятия решений на основе этих данных. Например, некоторые экономисты используют математическую логику для того, чтобы определить оптимальные пути для инвестиционных портфелей или для проектирования новых бизнес-стратегий.
В юриспруденции математическая логика используется для создания более точных и последовательных систем правовых решений. Например, внедрение электронных систем подачи заявлений и обработки данных может помочь упростить и ускорить судебные процессы.
Использование математической логики может помочь экономикам и юристам принимать более эффективные решения на основе четких и последовательных систем анализа данных. Благодаря этому сложные проблемы могут быть решены более эффективно и быстро, а это в свою очередь повышает производительность и качество работы в каждой области.