Что означает п в математике 6 класс

П показывает, что мы решаем задачи на положительные числа в математике 6 класса. Узнайте, как использовать п в уравнениях и примерах задач.

В математике 6 класса одним из ключевых понятий является «п». «П» в данном контексте обозначает периметр, который определяет длину границы многоугольника. Периметр является важным показателем для измерения длины объекта и решения различных задач.

Периметр можно найти, сложив длины всех сторон многоугольника. Например, чтобы найти периметр треугольника, необходимо сложить длины всех его сторон. Более сложные фигуры, такие как квадраты и прямоугольники, имеют равные стороны, что упрощает подсчет периметра. Однако, при работе с более сложными фигурами, такими как многоугольники, может потребоваться использование формулы для вычисления периметра.

Например, пусть у нас есть треугольник со сторонами длиной 4 см, 5 см и 7 см. Чтобы найти периметр этого треугольника, нужно сложить длины всех его сторон: 4 + 5 + 7 = 16 см. Таким образом, периметр треугольника равен 16 см.

Знание понятия «п» и умение вычислять периметр является неотъемлемой частью математического образования. Это позволяет ученикам измерять длину объектов, решать задачи и строить более сложные геометрические фигуры. Понимание понятия «п» также помогает развить математическую интуицию и логическое мышление.

В целом, понятие «п» является важным инструментом в изучении геометрии и математики в шестом классе. Научившись правильно использовать это понятие и решать задачи, ученики могут легко применять свои знания в повседневной жизни и в будущих учебных предметах, требующих математического мышления.

Понятие «п» в математике

Число «пи» является одним из наиболее известных и важных математических констант. Оно встречается во многих формулах и уравнениях, связанных с геометрией, тригонометрией, анализом и другими областями математики.

Число «пи» имеет множество интересных свойств и исторических деталей. Например, оно является бесконечной и непериодической десятичной дробью, и его точное значение нельзя выразить конечным числом цифр или дробью.

Благодаря своей универсальности и широкому применению, число «пи» является важным компонентом в различных областях науки и техники. Оно используется при решении задач в физике, инженерии, компьютерной графике, статистике и многих других дисциплинах.

Изучение числа «пи» является важной частью математического образования, и в школьной программе его изучают уже с начальных классов. Знание и понимание числа «пи» помогает ученикам развивать логическое мышление, аналитические навыки и понимание принципов математики.

Видео по теме:

Примеры использования «п» в математике

1. Периметр

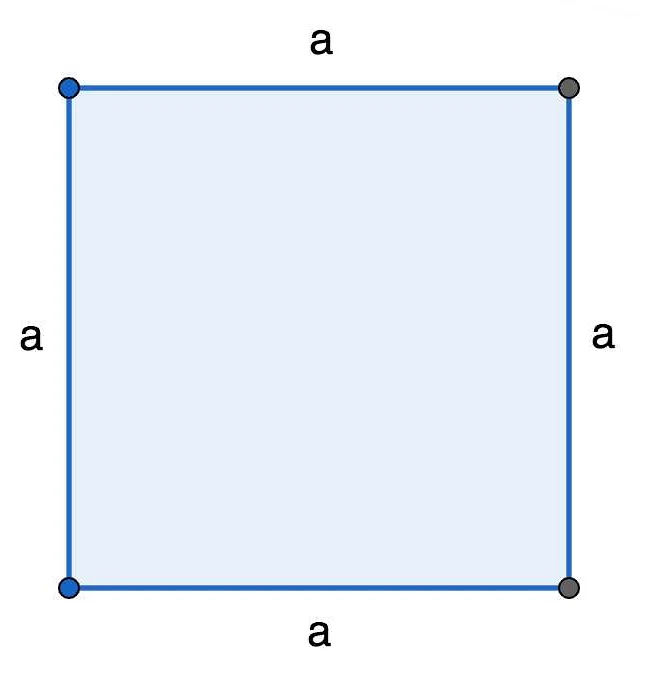
В математике «п» часто используется для обозначения периметра. Например, если дан квадрат со стороной «а», то его периметр можно выразить формулой «п = 4а».

2. Площадь

Также «п» может обозначать площадь различных фигур. Например, для круга радиуса «r» его площадь можно выразить формулой «п = πr^2», где «π» — математическая константа, примерно равная 3,14.

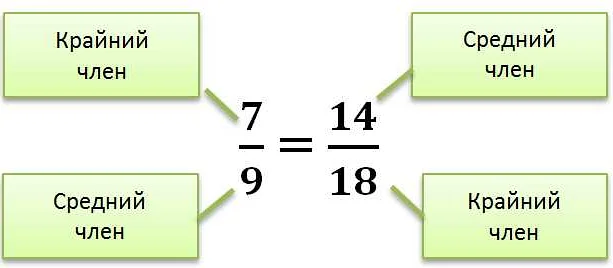
3. Пропорции

В задачах на пропорции «п» может обозначать неизвестное значение. Например, если две величины «а» и «б» пропорциональны, то можно записать «а/б = п/с», где «с» — третья величина, которую нужно найти.

ПримерыЗначение «п»

Периметр квадрата	п = 4а
Площадь круга	п = πr^2
Пропорции	а/б = п/с

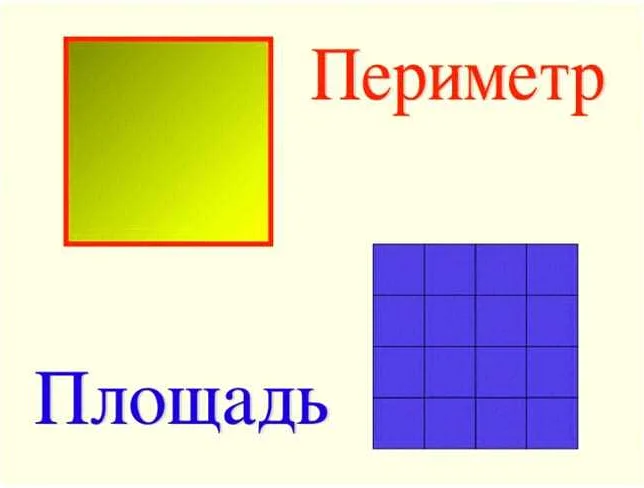
Площадь и периметр

Периметр — это сумма длин всех сторон фигуры. Он показывает, какой длины должна быть линия, чтобы обойти всю фигуру по ее контуру.

Например, для прямоугольника периметр можно найти, сложив длины всех его сторон. Если стороны прямоугольника имеют длины a и b, то периметр равен 2a + 2b.

Площадь — это понятие, которое показывает, сколько площади занимает поверхность фигуры.

Для прямоугольника площадь можно найти, умножив длину одной из его сторон на длину другой стороны. Если стороны прямоугольника имеют длины a и b, то площадь равна a * b.

Знание площади и периметра помогает понять, как измерять и сравнивать фигуры, а также решать математические задачи, связанные с геометрией.

Вопрос-ответ:

Что означает символ «п» в математике?

Символ «п» в математике обозначает число «пи» (π), которое является математической константой, представляющей отношение длины окружности к ее диаметру. В числовом выражении «пи» примерно равно 3,14, но имеет бесконечную десятичную дробь.

Зачем нужно знать значение «пи»?

Знание значения «пи» важно во многих областях математики и науки. Оно помогает решать задачи, связанные с окружностями, сферами, а также в геометрии и тригонометрии. «Пи» используется в формулах для вычисления площади круга, длины окружности и объема сферы.

Какая формула выражает отношение длины окружности к ее диаметру?

Отношение длины окружности к ее диаметру выражается формулой L = π * d, где «L» — длина окружности, «π» — число «пи», «d» — диаметр окружности. То есть, чтобы найти длину окружности, нужно умножить диаметр на «пи».

Как можно использовать значение «пи» в практических задачах?

Например, если вам нужно найти площадь круга, вы можете использовать формулу S = π * r^2, где «S» — площадь круга, «π» — число «пи», «r» — радиус круга. Для вычисления площади круга нужно возвести радиус в квадрат и умножить на «пи». Также «пи» может быть использовано для нахождения объема сферы и других формул, связанных с геометрией и тригонометрией.

Можно ли точно выразить значение «пи» в виде конечной десятичной дроби?

Нет, невозможно точно выразить значение «пи» в виде конечной десятичной дроби, потому что оно является бесконечной и иррациональной. Это означает, что его десятичная запись не повторяется и не может быть точно представлена конечным числом знаков после запятой.

Зачем нужно обозначение «п» в математике?

Обозначение «п» в математике используется для обозначения числа Пи, которое является одной из самых известных и важных математических констант. Оно используется для вычисления длины окружности и площади круга.

Как можно вычислить число Пи?

Число Пи является иррациональным числом, поэтому его невозможно точно вычислить. Однако существуют различные методы приближенного вычисления числа Пи, такие как метод Монте-Карло или использование ряда Лейбница. Например, ряд Лейбница выглядит следующим образом: 4 — 4/3 + 4/5 — 4/7 + 4/9 — 4/11 + … Чем больше членов ряда участвует в вычислении, тем точнее значение числа Пи получается.

Показатель степени

Показатель степени может быть как положительным, так и отрицательным. В случае положительного показателя степени, основание умножается на себя столько раз, сколько указано в показателе. Например, 2^3 = 2 * 2 * 2 = 8. В случае отрицательного показателя степени, основание берется в знаменатель дроби, а показатель степени меняет знак на противоположный. Например, 2^(-3) = 1/(2^3) = 1/8.

Показатель степени также может быть равен нулю. В этом случае результатом всегда будет 1. Например, 2^0 = 1.

Показатель степени широко используется в различных математических операциях и формулах, а также в науке и технике.

Построение графиков

Для построения графика необходимо иметь таблицу значений функции или уравнение, которое описывает зависимость. Затем можно построить координатную плоскость, где оси координат представляют значения независимой и зависимой переменных. Затем на основе таблицы значений или уравнения можно отметить точки на графике и соединить их линиями.

На графике можно определить такие характеристики функции, как нули функции, экстремумы, монотонность и периодичность. График также может помочь визуализировать и анализировать свойства функции и ее поведение в различных точках.

Примером построения графика может быть функция y = 2x + 1. Для этого необходимо выбрать некоторые значения для переменной x (например, -3, -2, -1, 0, 1, 2, 3), подставить их в уравнение и вычислить соответствующие значения для переменной y. Затем можно отметить эти точки на графике и соединить их линией.

xy

-3	-5
-2	-3
-1	-1
0	1
1	3
2	5
3	7

Проценты и вероятность

Еще одним значением «п» может быть вероятность. Вероятность — это число от 0 до 1, которое показывает, насколько событие возможно или невозможно. Например, если сказано, что вероятность выпадения грани «6» на игральной кости равна 1/6, это значит, что из шести возможных исходов один будет «6».

Использование процентов и вероятности широко распространено в реальной жизни и помогает нам делать различные расчеты и прогнозы. Понимание этих понятий поможет ученикам 6 класса лучше ориентироваться в информации и применять ее в решении задач.

Парабола и площадь треугольника

Площадь треугольника — это величина, которая показывает, сколько плоскости занимает данный треугольник. Площадь треугольника можно вычислить, используя формулу «полупериметр умножить на радикал из разности произведений полупериметра и длин сторон треугольника». Полупериметр треугольника равен сумме длин его сторон, деленной на 2.

Практическое применение «п»

Например, если нам известны длины сторон прямоугольника, мы можем найти его периметр, сложив длины всех сторон по формуле: прямоугольник = 2 * (а + b), где «а» и «b» — длины сторон прямоугольника.

Практическое применение «п» находится во множестве задач, связанных с расчетом периметра различных фигур: прямоугольников, квадратов, треугольников, кругов и т. д. Зная формулы для расчета периметра, можно легко находить значения периметра и использовать их в решении задач из реальной жизни.