Что такое многоугольник 4 класс математика

Многоугольник в математике — это фигура, состоящая из трех и более сторон. Ученики 4 класса учатся определять и классифицировать многоугольники, а также находить их периметр и площадь. В статье вы найдете подробное объяснение понятия многоугольника и примеры задач для самостоятельного решения.

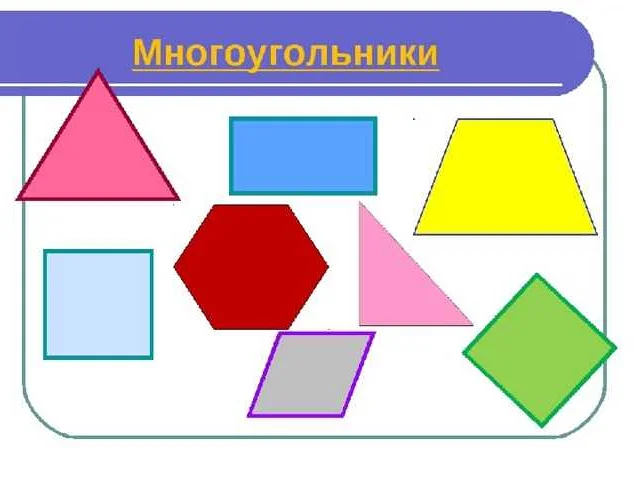
Многоугольник — это геометрическая фигура, которая состоит из отрезков, называемых сторонами, и вершин, в которых эти стороны пересекаются. Каждая сторона соединяет две соседние вершины, а каждая вершина является точкой пересечения двух сторон. Многоугольники могут иметь различное количество сторон и вершин, начиная от треугольника до многоугольников с более чем десятью сторонами.

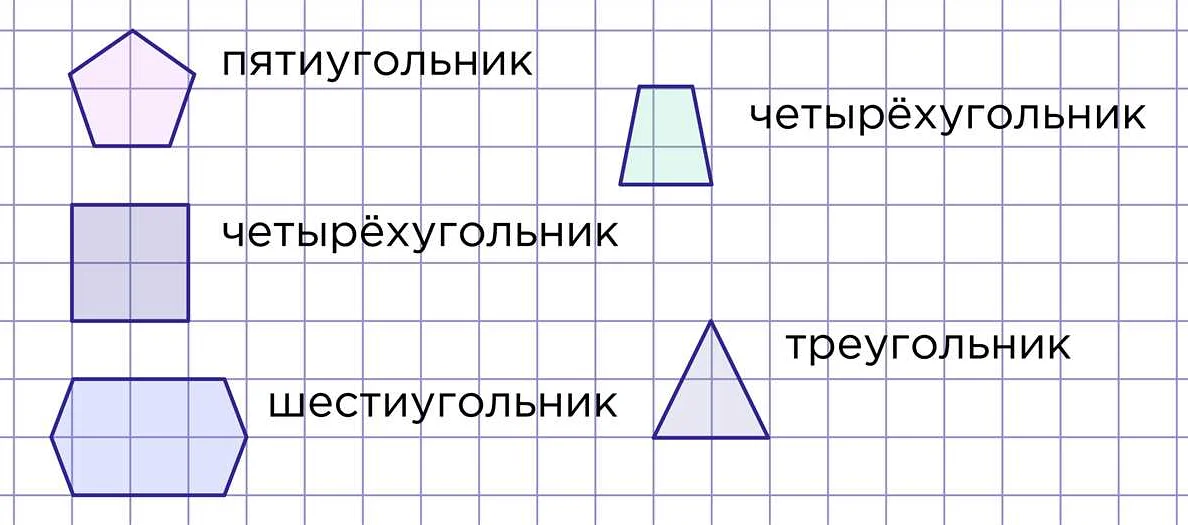
В 4 классе, ученики знакомятся с многоугольниками и учатся определять их по количеству сторон. Например, треугольник имеет три стороны и три вершины, четырехугольник — четыре стороны и четыре вершины, а пятиугольник — пять сторон и пять вершин. Ученики также учатся классифицировать многоугольники по типу: равносторонний, равнобедренный или произвольный.

Примеры многоугольников:

Треугольник — многоугольник с тремя сторонами и тремя вершинами. Все стороны могут быть разной длины, а углы — разной величины.

Четырехугольник — многоугольник с четырьмя сторонами и четырьмя вершинами. Он может быть прямоугольным, квадратом, параллелограммом или произвольным четырехугольником.

Пятиугольник — многоугольник с пятью сторонами и пятью вершинами. Углы и стороны пятиугольника могут быть различной формы и размера.

Разбираясь с определением и примерами многоугольников, ученики 4 класса становятся более знакомыми с геометрическими фигурами и приобретают навыки классификации и идентификации многоугольников.

Многоугольник 4 класс математика: определение и примеры

Многоугольник может быть выпуклым или невыпуклым. Выпуклый многоугольник имеет все углы меньше 180 градусов, а невыпуклый многоугольник имеет хотя бы один угол, больший 180 градусов.

Примеры многоугольников:

Треугольник – это многоугольник, состоящий из трех сторон и трех вершин. Все углы треугольника в сумме равны 180 градусов.

Четырехугольник – это многоугольник, состоящий из четырех сторон и четырех вершин. Четырехугольники могут быть различных типов: прямоугольник, квадрат, ромб, трапеция и т.д.

Пятиугольник – это многоугольник, состоящий из пяти сторон и пяти вершин.

Шестиугольник – это многоугольник, состоящий из шести сторон и шести вершин.

И так далее. Многоугольников может быть очень много разных видов, в зависимости от количества сторон и формы.

Изучение многоугольников в 4 классе помогает ученикам развивать навыки работы с геометрическими фигурами, а также понимание основных понятий и свойств многоугольников.

Видео по теме:

Определение многоугольника в математике для 4 класса

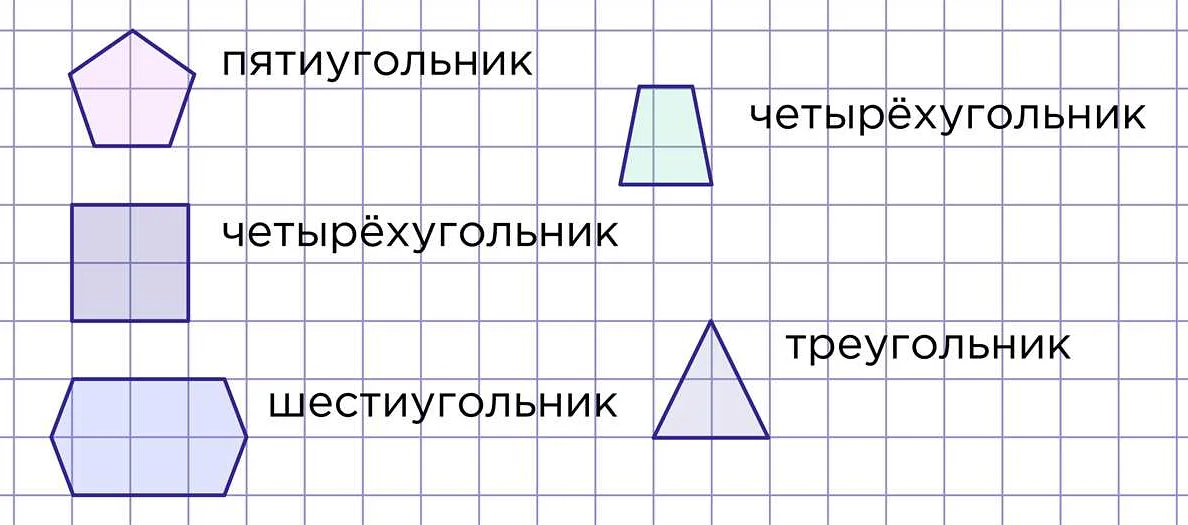
Многоугольники могут быть разных видов, например треугольник, четырехугольник, пятиугольник и так далее, в зависимости от количества сторон. Треугольник имеет три стороны и три вершины. Четырехугольник имеет четыре стороны и четыре вершины.

Каждый многоугольник имеет периметр — сумму длин всех его сторон. Например, для треугольника периметр будет равен сумме длин трех его сторон.

Также, многоугольники могут быть выпуклыми или невыпуклыми. Выпуклый многоугольник — это многоугольник, все вершины которого направлены в одну сторону. Невыпуклый многоугольник — это многоугольник, у которого хотя бы одна вершина направлена внутрь фигуры.

Многоугольники играют важную роль в геометрии и могут применяться для решения различных задач, например для нахождения периметра фигуры или площади многоугольника.

Свойства многоугольников в математике для 4 класса

Один из основных способов классификации многоугольников — это по их количеству сторон. В зависимости от числа сторон, многоугольники могут быть треугольниками, четырехугольниками, пятиугольниками и так далее. Треугольник имеет 3 стороны, четырехугольник — 4 стороны и так далее.

Другим важным свойством многоугольников является сумма внутренних углов. Внутренний угол многоугольника — это угол, образованный двумя соседними сторонами многоугольника. Сумма внутренних углов в многоугольнике всегда равна (n-2) * 180 градусов, где n — число сторон многоугольника. Например, для треугольника сумма внутренних углов будет равна (3-2) * 180 = 180 градусов, для четырехугольника — (4-2) * 180 = 360 градусов.

Кроме того, многоугольники могут быть выпуклыми и невыпуклыми. Выпуклый многоугольник — это многоугольник, у которого все внутренние углы меньше 180 градусов. Невыпуклый многоугольник имеет хотя бы один внутренний угол больше 180 градусов.

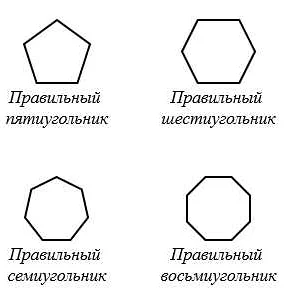
Также, многоугольники могут быть правильными и неправильными. Правильный многоугольник имеет все стороны и углы одинаковой длины, в то время как неправильный многоугольник имеет разные стороны и углы.

Важно понимать, что свойства многоугольников могут иметь практическое применение. Например, знание суммы внутренних углов многоугольника может помочь в решении задач на геометрическую конструкцию и нахождение неизвестных углов.

Изучение свойств многоугольников позволяет нам лучше понять геометрию и решать задачи, связанные с этой темой. Узнайте больше о многоугольниках и их свойствах, чтобы стать лучшим в решении задач математики для 4 класса!

Примеры многоугольников в математике для 4 класса

Вот некоторые примеры многоугольников:

1. Треугольник – это многоугольник, который имеет три стороны и три вершины. Примером треугольника может быть флаг страны Мексика.

2. Четырехугольник – это многоугольник, который имеет четыре стороны и четыре вершины. Примером четырехугольника может быть книга.

3. Пятиугольник – это многоугольник, который имеет пять сторон и пять вершин. Примером пятиугольника может быть звезда.

4. Шестиугольник – это многоугольник, который имеет шесть сторон и шесть вершин. Примером шестиугольника может быть снежинка.

5. Многоугольник с более чем шестью сторонами называется многоугольником с «n» сторонами. Примером многоугольника с «n» сторонами может быть многоугольник с восьмью сторонами, также известный как восьмиугольник.

Это лишь некоторые примеры многоугольников, которые вы изучите в математике для 4 класса. Узнавая об этих геометрических фигурах, вы сможете лучше понять их свойства и использовать их в решении задач.

Как определить тип многоугольника в математике для 4 класса

Для определения типа многоугольника в математике для 4 класса необходимо учитывать их количество сторон и углов. В зависимости от этих характеристик можно определить следующие типы многоугольников:

Треугольник — многоугольник, который имеет три стороны и три угла.

Четырехугольник — многоугольник, который имеет четыре стороны и четыре угла.

Пятиугольник — многоугольник, который имеет пять сторон и пять углов.

Шестиугольник — многоугольник, который имеет шесть сторон и шесть углов.

Семиугольник — многоугольник, который имеет семь сторон и семь углов.

Восьмиугольник — многоугольник, который имеет восемь сторон и восемь углов.

Девятиугольник — многоугольник, который имеет девять сторон и девять углов.

Десятиугольник — многоугольник, который имеет десять сторон и десять углов.

Таким образом, зная количество сторон и углов, можно определить тип многоугольника в математике для 4 класса.

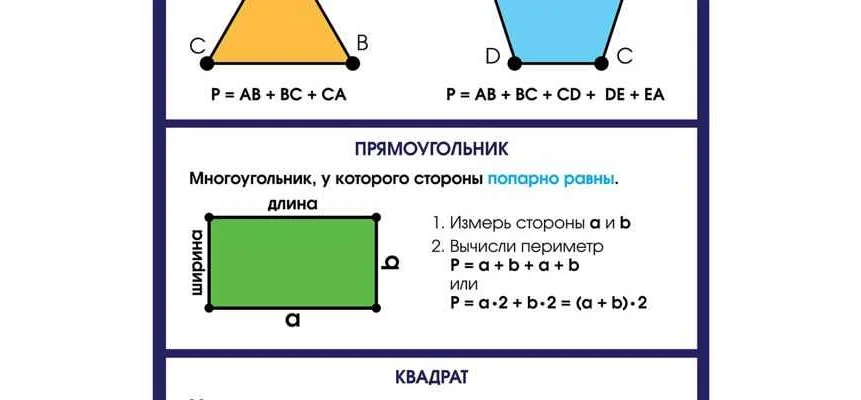
Как найти периметр многоугольника в математике для 4 класса

Для примера, рассмотрим простой многоугольник — треугольник. У треугольника есть три стороны. Если известны длины всех сторон треугольника, то периметр можно найти, сложив длины всех трех сторон.

Например, у треугольника со сторонами длиной 5, 7 и 9, периметр будет равен 5 + 7 + 9 = 21.

Для любого многоугольника, чтобы найти его периметр, нужно знать длины всех его сторон. Если длины сторон неизвестны, их можно измерить с помощью линейки или вычислить, используя геометрические формулы.

Зная периметр многоугольника, можно сравнивать его с другими многоугольниками, определять их свойства и решать различные задачи, связанные с многоугольниками.

Как найти площадь многоугольника в математике для 4 класса

Для нахождения площади многоугольника нужно знать его форму и размеры сторон. В 4 классе изучаются простые многоугольники, в которых все стороны и углы равны.

Существует несколько способов нахождения площади многоугольника. Один из них — разделение многоугольника на прямоугольники и треугольники, нахождение их площадей и сложение полученных значений. Другой способ — использование формулы площади многоугольника, зависящей от его формы.

Например, для прямоугольника площадь можно найти, умножив длину одной из сторон на длину другой стороны.

Для треугольника площадь можно найти, используя формулу «площадь = (основание * высоту) / 2», где основание — одна из сторон треугольника, а высота — перпендикуляр, опущенный из вершины треугольника на основание.

Если многоугольник имеет сложную форму, его площадь можно приближенно найти, разбив его на более простые фигуры, нахождение площадей которых изучается в 4 классе.

Важно помнить, что для точного нахождения площади многоугольника нужно знать все его размеры и формулы для вычисления площадей простых фигур, из которых он состоит.

Знание и умение находить площадь многоугольника — важные навыки в математике, которые помогут в решении задач и понимании геометрических фигур.

Где применяются многоугольники в реальной жизни

Один из наиболее распространенных примеров использования многоугольников – это строительство. Архитекторы и инженеры часто используют многоугольники для проектирования зданий и сооружений. Они могут использовать многоугольники для определения формы и размеров здания, планирования расположения помещений и создания пространственных композиций.

Многоугольники также часто используются в картографии. Картографы используют многоугольники для представления формы и границ различных территорий. Например, многоугольники могут использоваться для обозначения границ стран или регионов на карте.

Еще одной областью, где многоугольники находят применение, является компьютерная графика. Программисты и дизайнеры используют многоугольники для создания трехмерных моделей объектов, а также для отрисовки и текстурирования поверхностей.

Многоугольники также используются в играх. В компьютерных играх многоугольники используются для создания графических объектов и сцен, а также для определения коллизий между объектами.

В искусстве также можно встретить использование многоугольников. Художники и дизайнеры могут использовать многоугольники для создания уникальных композиций и геометрических узоров.

Кроме того, многоугольники можно встретить в различных играх и головоломках, которые помогают развивать логическое мышление и пространственное воображение.

Таким образом, многоугольники имеют широкое применение в реальной жизни и играют важную роль в различных областях, от строительства и картографии до компьютерной графики и искусства.

Вопрос-ответ:

Как определить многоугольник в математике?

Многоугольник — это геометрическая фигура, состоящая из трех или более сторон, которые образуют замкнутую фигуру. Каждая сторона многоугольника встречается ровно два раза в вершинах.

Какие есть примеры многоугольников?

Примеры многоугольников: треугольник (3 стороны), квадрат (4 стороны), пятиугольник (5 сторон), шестиугольник (6 сторон) и так далее.

Как можно классифицировать многоугольники?

Многоугольники можно классифицировать по количеству сторон. Например, треугольник — многоугольник с тремя сторонами, четырехугольник — с четырьмя сторонами и так далее.

Какие свойства имеют многоугольники?

У многоугольников есть несколько свойств. Например, сумма всех внутренних углов многоугольника равна сумме 180 градусов у каждого угла. Также, сумма длин всех сторон многоугольника называется периметром.