Что означает равенство в математике
Содержимое
- 1 Что означает равенство в математике
- 1.1 Равенство в математике: основные понятия и принципы
- 1.2 Видео по теме:
- 1.3 Определение равенства
- 1.4 Символы равенства
- 1.5 Операции с равенством
- 1.6 Свойства равенства
- 1.7 Понятие эквивалентности в математике
- 1.8 Доказательство равенства
- 1.9 Примеры применения равенства
- 1.10 Равенство в математических моделях
- 1.11 Вопрос-ответ:
Равенство в математике – это понятие, которое описывает ситуацию, когда два математических выражения или объекта являются одинаковыми или эквивалентными. Узнайте, что означает равенство в математике и как его использовать в решении уравнений и задач.
Равенство — одно из ключевых понятий в математике, которое играет важную роль в различных областях этой науки. Оно позволяет устанавливать соответствие между различными объектами и явлениями, а также проводить различные операции и выводы, основанные на этом соответствии.
В математике равенство обозначается знаком «=» и используется для указания того, что два объекта или выражения имеют одинаковое значение. Однако равенство в математике имеет свои особенности и правила, которые необходимо соблюдать при его использовании.
Принцип равенства в математике гласит о том, что если два объекта или выражения равны между собой, то можно заменить одно на другое в любом математическом выражении без изменения его значения. Это значит, что равенство является отношением симметричным и транзитивным.
Например, если у нас есть выражение «2 + 3 = 5», то мы можем заменить его на «5 = 5» или «2 + 3 + 0 = 5», так как все эти выражения имеют одно и то же значение.
Равенство в математике также имеет свои особенности в зависимости от типа объектов или выражений, которые сравниваются. Например, для чисел равенство означает, что они имеют одинаковое значение. Для геометрических фигур равенство означает, что они имеют одинаковую форму и размеры.
В заключение, равенство в математике — это важное понятие, которое позволяет проводить различные операции и выводы, основанные на соответствии между объектами и выражениями. Правильное использование равенства в математике является одним из ключевых принципов этой науки.
Равенство в математике: основные понятия и принципы

В математике равенство обозначается знаком «=», который читается как «равно». При использовании знака равенства, две стороны уравнения объявляются равными между собой.
Принцип равенства в математике состоит в том, что любую операцию, которую мы применяем к одной стороне уравнения, должны также применить и к другой стороне уравнения. Это позволяет нам сохранить равенство и получить правильный результат.
В математических уравнениях равенство используется для нахождения неизвестных величин. Если имеется уравнение вида «a = b», то мы можем выразить неизвестную величину, подставив значение, равное «b», вместо «a».
Равенство также играет важную роль в доказательствах и решении математических задач. С помощью равенства мы можем установить связь между различными объектами и операциями, а также проверить справедливость различных математических утверждений.
В заключение, равенство является одним из фундаментальных понятий в математике. Оно позволяет нам сравнивать и анализировать различные объекты и выражения, а также решать уравнения и доказывать математические утверждения.
Видео по теме:
Определение равенства
Если два выражения, например «а» и «b», равны между собой, то они обладают одинаковыми числовыми значениями или идентичными структурами. Иначе говоря, значения выражений «а» и «b» равны.
Равенство в математике имеет несколько свойств:
- Симметричность: Если «а» равно «b», то «b» равно «а».
- Транзитивность: Если «а» равно «b», и «b» равно «с», то «а» равно «с».
- Рефлексивность: Любой объект или выражение равно самому себе.
Равенство играет важную роль в математике и используется во многих областях, таких как алгебра, геометрия и анализ. Оно позволяет устанавливать связи между различными математическими объектами и решать уравнения, системы уравнений и другие задачи.
Символы равенства

Например, если у нас есть выражение «2 + 2 = 4», это означает, что результат сложения числа 2 и числа 2 равен числу 4.
В некоторых случаях используются также другие символы равенства. Например, символ «~=» используется для обозначения приближенного равенства. Это означает, что два значения близки друг к другу, но не совпадают абсолютно точно.
Еще один пример символа равенства — «≡». Он используется для обозначения тождественного равенства. Это означает, что два выражения имеют одинаковые значения во всех возможных случаях.
Иногда в математике используются и другие символы равенства, такие как «≈» (приближенное равенство), «≠» (неравенство) и другие.
Важно понимать, что символы равенства в математике обозначают не только числовое равенство, но и равенство между выражениями, функциями и другими математическими объектами.
Операции с равенством
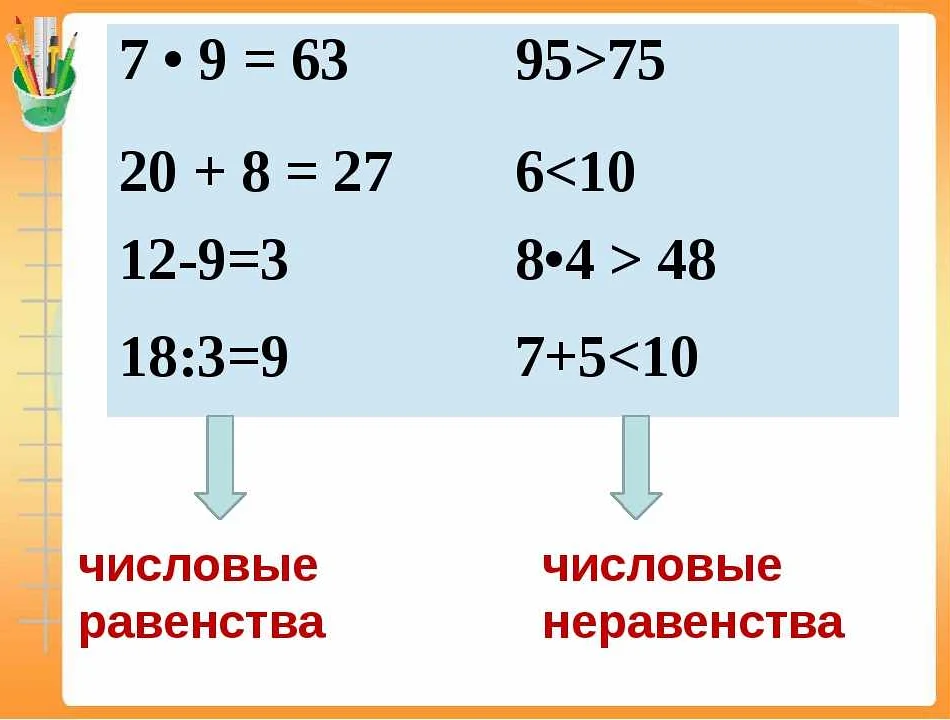
Одной из операций, связанных с равенством, является операция сложения. Если два выражения равны, то их суммы также будут равными. Например, если a = b и c = d, то a + c = b + d.
Другой операцией, связанной с равенством, является операция вычитания. Если два выражения равны, то их разности также будут равными. Например, если a = b и c = d, то a — c = b — d.
Также равенство подчиняется операции умножения. Если два выражения равны, то их произведения также будут равными. Например, если a = b и c = d, то a * c = b * d.
Наконец, операция деления также применима к равенству. Если два выражения равны, то их частное также будет равным. Например, если a = b и c = d, то a / c = b / d.
Необходимо отметить, что при применении операций к равенству, важно соблюдать правила алгебры и сохранять равенство, чтобы получить корректный результат.
Свойства равенства
1. Рефлексивность: Любое число или объект всегда равно самому себе. Например, для любого числа а, а = а.
2. Симметричность: Если a равно b, то b также равно a. Например, если а = b, то b = а.
3. Транзитивность: Если a равно b и b равно c, то a также равно c. Например, если а = b и b = c, то a = c.
4. Замена: Если a равно b, то a можно заменить на b и наоборот без изменения истинности утверждения. Например, если а = b, то у нас есть следующая замена: a + c = b + c.
5. Добавление и вычитание: Если a равно b, то a плюс или минус любое число равно b плюс или минус то же число. Например, если а = b, то a + c = b + c и a — c = b — c.
6. Умножение и деление: Если a равно b, то a умножить или разделить на любое число равно b умножить или разделить на то же число, за исключением нуля. Например, если а = b, то a * c = b * c и a / c = b / c (при условии, что c ≠ 0).
Эти свойства равенства играют важную роль в математике и позволяют нам выполнять различные операции и преобразования с уравнениями и неравенствами.
Понятие эквивалентности в математике
В математике эквивалентность можно определить как отношение, которое обладает следующими свойствами:
- Рефлексивность: каждый элемент эквивалентен самому себе.
- Симметричность: если элемент A эквивалентен элементу B, то элемент B также эквивалентен элементу A.
- Транзитивность: если элемент A эквивалентен элементу B, и элемент B эквивалентен элементу C, то элемент A эквивалентен элементу C.
Также важно отметить, что эквивалентность может быть определена в различных контекстах с использованием разных критериев. Например, в алгебре два элемента могут считаться эквивалентными, если они обладают одними и теми же алгебраическими свойствами или операциями. В геометрии два геометрических объекта могут быть эквивалентными, если они имеют одинаковые формы или размеры.
Понимание эквивалентности является фундаментальным для различных областей математики и служит основой для множества математических концепций и теорем. Это понятие позволяет математикам проводить сравнения, устанавливать связи и классифицировать объекты в математических структурах.
Доказательство равенства
Одним из основных методов доказательства равенства является применение математических операций и свойств равенства. Например, чтобы доказать равенство двух выражений, можно последовательно применять операции сложения, вычитания, умножения и деления, используя свойства равенства, такие как коммутативность, ассоциативность и дистрибутивность.
Другим методом доказательства равенства является использование математических тождеств и эквивалентных преобразований. Тождество — это утверждение, которое верно для любых значений переменных. Используя тождества, можно преобразовать одно выражение в другое, показав их равенство.
В доказательстве равенства часто используются логические операции, такие как импликация (если-то) и обратная импликация (то-если). При доказательстве равенства необходимо проводить логические выводы, объяснять каждый шаг и описывать использованные свойства, операции и тождества.
Доказательство равенства имеет важное значение в математике, так как позволяет строить систематические и надежные математические аргументы. Оно также позволяет установить связь между различными математическими объектами и утверждениями, что способствует развитию математического знания и решению сложных задач.
Примеры применения равенства

Одним из примеров применения равенства является решение уравнений. Уравнение — это математическое выражение, в котором присутствуют неизвестные величины и знак равенства. Для нахождения значения неизвестной величины необходимо решить уравнение, то есть найти такое значение, при котором обе его части будут равны. Например, уравнение «2x + 5 = 13» имеет решение x = 4.
Еще одним примером применения равенства является доказательство тождеств. Тождество — это утверждение, которое справедливо для всех значений переменных, участвующих в нем. Чтобы доказать тождество, необходимо показать, что его правая и левая части равны друг другу. Например, тождество «a^2 — b^2 = (a + b)(a — b)» можно доказать, разложив правую часть на множители и упростив полученное выражение до левой части.
Кроме того, равенство используется в математических операциях, таких как сложение, вычитание, умножение и деление. Например, для сложения двух чисел a и b выполняется равенство a + b = b + a. Данное свойство коммутативности сложения можно использовать для перестановки слагаемых в выражении, не изменяя его значения.
Таким образом, равенство является важным понятием в математике, которое применяется в различных контекстах и задачах, таких как решение уравнений, доказательство тождеств и выполнение математических операций.
Равенство в математических моделях

Равенство играет важную роль в математических моделях, которые описывают различные явления и процессы. В математической модели равенство используется для установления соответствия между объектами или явлениями.
В математических моделях равенство может иметь разные значения в зависимости от контекста. Например, в алгебре равенство обозначает, что два математических выражения имеют одинаковое значение. В геометрии равенство может означать, что две фигуры имеют одинаковые размеры или формы.
Равенство в математических моделях обладает рядом важных свойств. Одно из основных свойств равенства — это транзитивность. Это значит, что если два объекта равны друг другу, а третий объект равен одному из этих двух, то третий объект равен и другому объекту. Например, если a = b и b = c, то можно сделать вывод, что a = c.
Еще одно важное свойство равенства — это рефлексивность. Это означает, что каждый объект равен самому себе. Например, a = a.
Равенство в математических моделях может быть использовано для решения различных задач. Например, уравнения используются для нахождения неизвестных значений переменных. Равенство также используется в доказательствах математических теорем и утверждений.
В заключение, равенство в математических моделях является важным понятием, которое позволяет установить соответствие между объектами или явлениями. Оно обладает свойствами транзитивности и рефлексивности, и может быть использовано для решения задач и доказательства теорем.
Вопрос-ответ:
Что такое равенство в математике?
Равенство в математике — это понятие, которое означает, что два выражения или объекта имеют одинаковое значение или идентичны.
Какие основные принципы лежат в основе понятия равенства в математике?
Основные принципы равенства в математике включают принцип симметрии (если a=b, то b=a), принцип транзитивности (если a=b и b=c, то a=c) и принцип замены (если a=b, то можно заменить a на b и наоборот в любом выражении без изменения его значения).
Какими символами обозначается равенство в математике?
Равенство в математике обозначается символом «=».
Какие другие понятия связаны с равенством в математике?
С равенством в математике связаны такие понятия, как неравенство (когда два объекта или выражения не имеют одинакового значения), эквивалентность (когда два выражения имеют одинаковые значения, но могут иметь различный вид) и тождество (когда два выражения полностью идентичны).

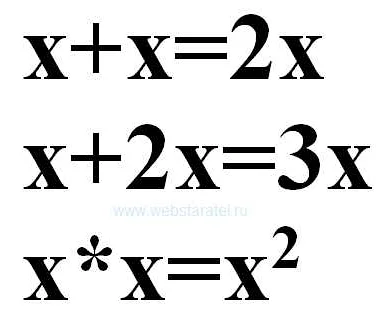
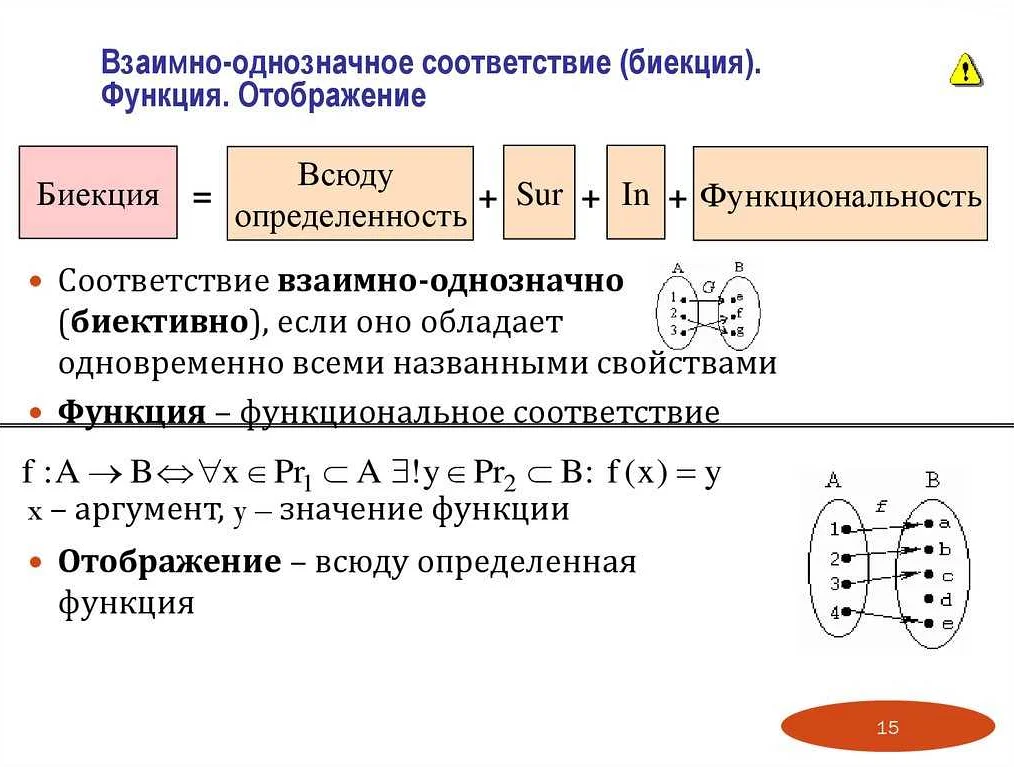


Статья очень понравилась! Она дала мне ясное представление о том, что такое равенство в математике. Я узнала, что равенство — это основной принцип, который используется во всех областях математики. Мне было интересно узнать о различных типах равенств, таких как числовое равенство и символическое равенство. Я также узнала о важности проверки равенства и использования доказательства для подтверждения его истинности. Статья была очень информативной и понятной. Я с удовольствием прочитала ее и теперь имею более глубокое понимание равенства в математике. Большое спасибо за такую интересную статью!