Что такое соответствие в математике
Содержимое
- 1 Что такое соответствие в математике
- 1.1 Что значит соответствие в математике?
- 1.2 Какие бывают типы соответствий в математике?
- 1.3 Какие свойства имеет соответствие в математике?
- 1.4 Какие примеры соответствий можно привести?
- 1.5 Как определить обратное соответствие?
- 1.6 Какие свойства имеет обратное соответствие?
- 1.7 Примеры обратных соответствий в математике
- 1.8 Как применяется понятие соответствия в математике на практике?
- 1.9 Видео по теме:
Соответствие в математике — это отношение, которое устанавливает соотношение между элементами двух множеств. Оно позволяет определить, каким образом каждому элементу одного множества соответствует элемент другого множества. Узнайте, как работает соответствие и как его применяют в математических задачах и теории.
Соответствие — одно из основных понятий в математике, которое описывает связь между двумя множествами и позволяет установить соотношение между их элементами. Соответствие можно представить в виде таблицы, где каждому элементу первого множества сопоставлен элемент второго множества. Такая связь может быть однозначной или многозначной.
Соответствие может быть задано различными способами, например, графически, словесно или символически. Оно играет важную роль во многих областях математики, таких как алгебра, геометрия, теория вероятностей и др. Соответствие позволяет решать задачи, связанные с сопоставлением и классификацией объектов.
Например, в геометрии соответствие может быть установлено между точками на плоскости и числами, которые задают координаты этих точек. Такое соответствие позволяет определять расстояние между точками, проводить геометрические построения и решать другие задачи.
Соответствие — важный инструмент в математике, который помогает структурировать информацию, устанавливать зависимости и решать различные задачи. Понимание понятия соответствия позволяет более глубоко изучить различные математические области и применять их в решении практических задач.
Что значит соответствие в математике?
В математике понятие соответствия используется для описания отношения между элементами двух множеств. Соответствие определяет связь между элементами первого множества (называемого исходным или областью определения) и элементами второго множества (называемого множеством значений или областью значений).
Соответствие можно представить в виде таблицы или графика, где каждому элементу исходного множества соответствует один или несколько элементов множества значений. Например, если имеется множество животных и множество их классификаций, то соответствие может быть описано так: каждому животному соответствует его классификация.
Соответствие в математике играет важную роль во многих областях, таких как теория множеств, алгебра, геометрия и дискретная математика. Оно позволяет описывать и анализировать взаимосвязи между элементами различных множеств, что является фундаментальным в математике.
Какие бывают типы соответствий в математике?
В математике существует несколько типов соответствий, которые используются для установления связи между двумя множествами. Рассмотрим основные из них:
- Однозначное соответствие: в этом типе соответствия каждому элементу из одного множества соответствует ровно один элемент из другого множества. Например, функция y = x^2 устанавливает однозначное соответствие между множеством действительных чисел x и множеством их квадратов y.
- Многозначное соответствие: здесь каждому элементу из одного множества может соответствовать несколько элементов из другого множества. Например, функция y = sin(x) устанавливает многозначное соответствие между множеством действительных чисел x и множеством их синусов y.
- Обратное соответствие: это соответствие, при котором элементы одного множества соответствуют элементам другого множества и наоборот. Например, функция y = x^3 устанавливает обратное соответствие между множеством действительных чисел x и множеством их кубов y.
- Частичное соответствие: это соответствие, при котором не все элементы одного множества имеют соответствие в другом множестве. Например, функция y = sqrt(x) устанавливает частичное соответствие между множеством действительных чисел x и множеством их квадратных корней y, так как квадратный корень из отрицательного числа не определен в действительных числах.
- Полное соответствие: это соответствие, при котором каждый элемент одного множества имеет соответствие в другом множестве. Например, функция y = x устанавливает полное соответствие между множеством действительных чисел x и множеством самих себя, так как каждому числу из одного множества соответствует точно такое же число из другого множества.
Различные типы соответствий в математике имеют свои особенности и применяются в различных областях математики и ее приложениях. Понимание этих типов соответствий помогает в решении различных математических задач и построении моделей.
Какие свойства имеет соответствие в математике?
Соответствие в математике обладает несколькими важными свойствами:
| 1. Однозначность | Каждому элементу из одного множества соответствует ровно один элемент из другого множества. Это означает, что нет ситуаций, когда одному элементу можно сопоставить несколько элементов или наоборот. |
| 2. Обратимость | Соответствие может быть обратимым, то есть каждому элементу из одного множества можно сопоставить элемент из другого множества, и наоборот. При этом соответствие обратно сопоставляет элементы в обратном порядке. |
| 3. Зависимость от порядка | Порядок элементов в соответствии важен. Если элементы поменять местами, то соответствие может измениться. |
| 4. Полнота | Соответствие может быть полным, если каждому элементу из одного множества сопоставлен элемент из другого множества. В противном случае, оно называется частичным. |
| 5. Существование обратного соответствия | Если для каждого элемента из одного множества существует элемент из другого множества, то соответствие называется существующим обратным соответствием. В противном случае, оно называется несуществующим обратным соответствием. |
Эти свойства помогают определить и описывать соответствия в математике и играют важную роль в различных областях этой науки.
Какие примеры соответствий можно привести?
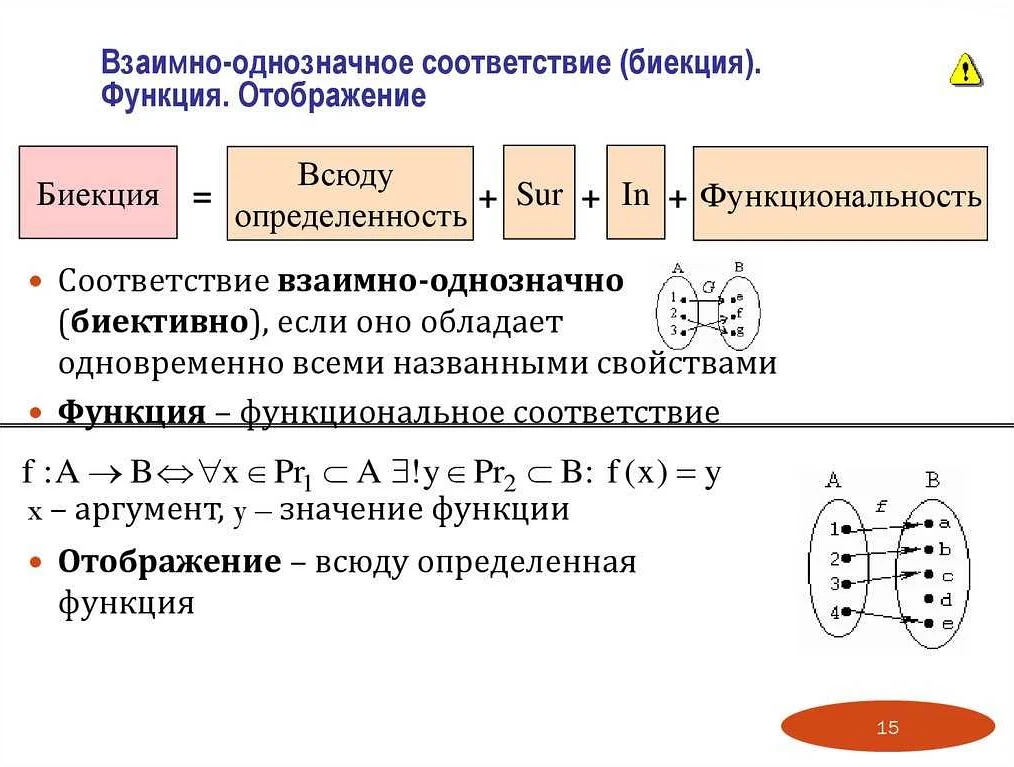
В математике соответствие может быть представлено различными способами. Вот несколько примеров:
1. Соответствие между множествами. Например, можно рассмотреть соответствие между множеством студентов и множеством их оценок по математике. Каждому студенту соответствует определенная оценка. Такое соответствие можно представить в виде таблицы или графика.
2. Функциональное соответствие. В этом случае каждому элементу из одного множества соответствует ровно один элемент из другого множества. Например, можно рассмотреть соответствие между множеством студентов и их возрастом. Каждому студенту соответствует определенный возраст, и каждому возрасту соответствует определенное количество студентов.
3. Геометрическое соответствие. Это соответствие может быть представлено в виде геометрической фигуры или пространственного объекта. Например, можно рассмотреть соответствие между точками на плоскости и их координатами. Каждой точке на плоскости соответствуют определенные значения координат по оси X и по оси Y.
Все эти примеры демонстрируют, как соответствие может быть использовано для описания связи между различными математическими объектами и явлениями. Соответствие является важным инструментом в математике и широко используется для решения различных задач и построения моделей.
Как определить обратное соответствие?
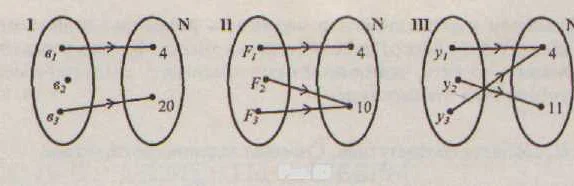
Для определения обратного соответствия необходимо выполнить следующие шаги:
- Определить исходное соответствие.
- Заменить значения и аргументы соответствия местами.
- Записать полученное обратное соответствие.
Например, рассмотрим исходное соответствие между множеством студентов и их оценками:
СтудентОценка
| Алексей | 4 |
| Мария | 5 |
| Иван | 3 |
Для определения обратного соответствия необходимо заменить значения и аргументы соответствия местами:
ОценкаСтудент
| 4 | Алексей |
| 5 | Мария |
| 3 | Иван |
Таким образом, получаем обратное соответствие между оценками и студентами. Обратное соответствие может использоваться для определения студентов, которые получили определенную оценку.
Какие свойства имеет обратное соответствие?
Обратное соответствие обладает следующими свойствами:
- У обратного соответствия множества-источник и множество-цель меняются ролями. То есть, если в исходном соответствии элементы одного множества являются первыми компонентами пар, то в обратном соответствии эти элементы будут вторыми компонентами пар.
- Обратное соответствие существует только в том случае, если исходное соответствие является взаимооднозначным, то есть каждому элементу первого множества соответствует единственный элемент второго множества.
- При наличии обратного соответствия между двумя множествами можно строить композицию соответствий. То есть, если задано соответствие A между множествами А и В, и соответствие B между множествами В и С, то можно определить обратное соответствие B°A между множествами С и А.
Обратное соответствие является важным понятием в математике и находит применение в различных областях, таких как алгебра, теория множеств, геометрия и другие.
Примеры обратных соответствий в математике
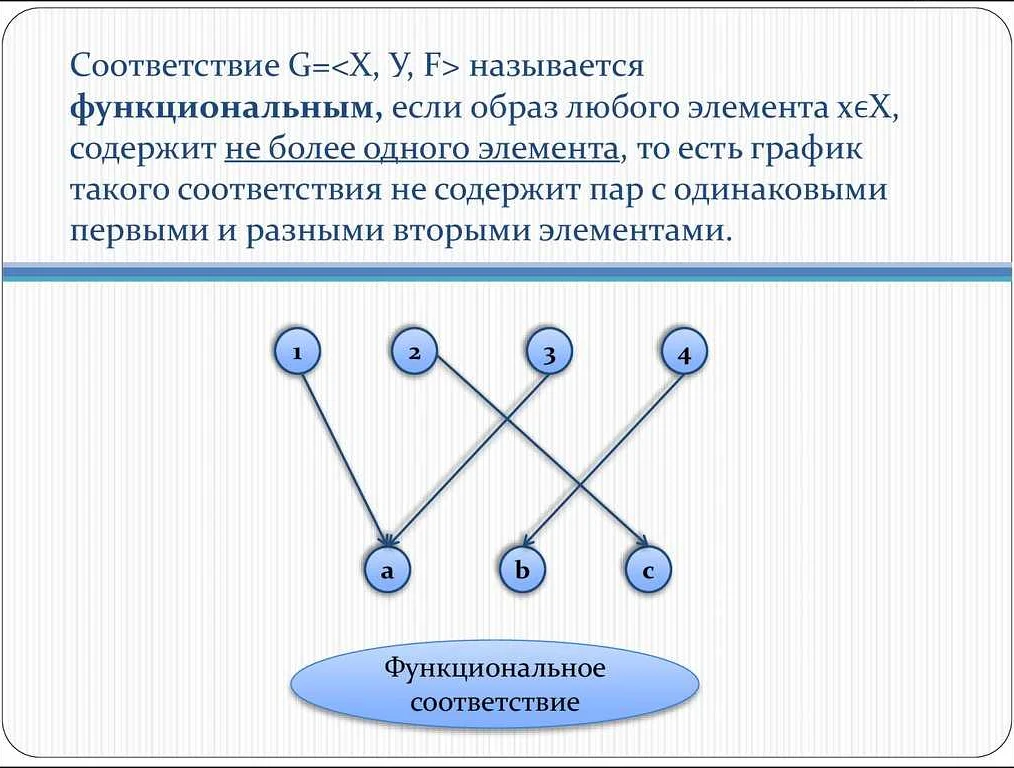
Примеры обратных соответствий в математике:
- Обратное соответствие между множеством натуральных чисел и множеством целых чисел. Каждому натуральному числу соответствует ровно одно целое число, и наоборот, каждому целому числу соответствует ровно одно натуральное число.
- Обратное соответствие между множеством точек на плоскости и множеством пар координат (x, y). Каждой точке на плоскости соответствует ровно одна пара координат, и наоборот, каждой паре координат (x, y) соответствует ровно одна точка на плоскости.
- Обратное соответствие между множеством букв русского алфавита и множеством чисел от 1 до 33. Каждой букве русского алфавита соответствует ровно одно число от 1 до 33, и наоборот, каждому числу от 1 до 33 соответствует ровно одна буква русского алфавита.
Это лишь некоторые из множества примеров обратных соответствий в математике. Обратные соответствия играют важную роль в различных областях математики, а также в других науках.
Как применяется понятие соответствия в математике на практике?

В математике соответствия используются, например, при решении задач на комбинаторику, графы, алгебру и другие области. Они позволяют установить соответствие между объектами и их характеристиками, исходя из заданных условий.
Для наглядного представления соответствия в математике на практике часто используют таблицы. В таблице соответствия приводятся два множества и указывается, какие элементы одного множества соответствуют элементам другого множества.
Множество AМножество B
| Элемент a | Элемент b |
| Элемент c | Элемент d |
| Элемент e | Элемент f |
В данной таблице можно увидеть, что элементы множества A (a, c, e) соответствуют элементам множества B (b, d, f). Такое соответствие может быть полным, когда каждому элементу одного множества соответствует элемент другого множества, или частичным, когда только некоторые элементы одного множества соответствуют элементам другого множества.
Соответствие в математике также может использоваться для построения функций. Функция является особым видом соответствия, в котором каждому элементу множества A соответствует ровно один элемент множества B. Функции широко применяются для описания зависимостей между величинами и решения различных задач.
Таким образом, понятие соответствия играет важную роль в математике и находит применение на практике для решения различных задач и построения функций.
Видео по теме:
Что такое соответствие в математике?
Соответствие в математике — это связь, установленная между элементами двух множеств, при которой каждому элементу одного множества сопоставляется единственный элемент другого множества.
Какие примеры соответствий в математике можно привести?
Примерами соответствий в математике могут служить пары чисел, где каждому числу из первого множества сопоставлено единственное число из второго множества. Например, соответствие между множествами {1, 2, 3} и {a, b, c}, где 1 соответствует a, 2 — b, 3 — c.
Каким образом можно представить соответствие в математике?
Соответствие в математике можно представить с помощью таблиц, графиков, диаграмм и формул. Например, таблица соответствия может содержать две колонки, в первой — элементы первого множества, а во второй — элементы второго множества, которым они соответствуют.
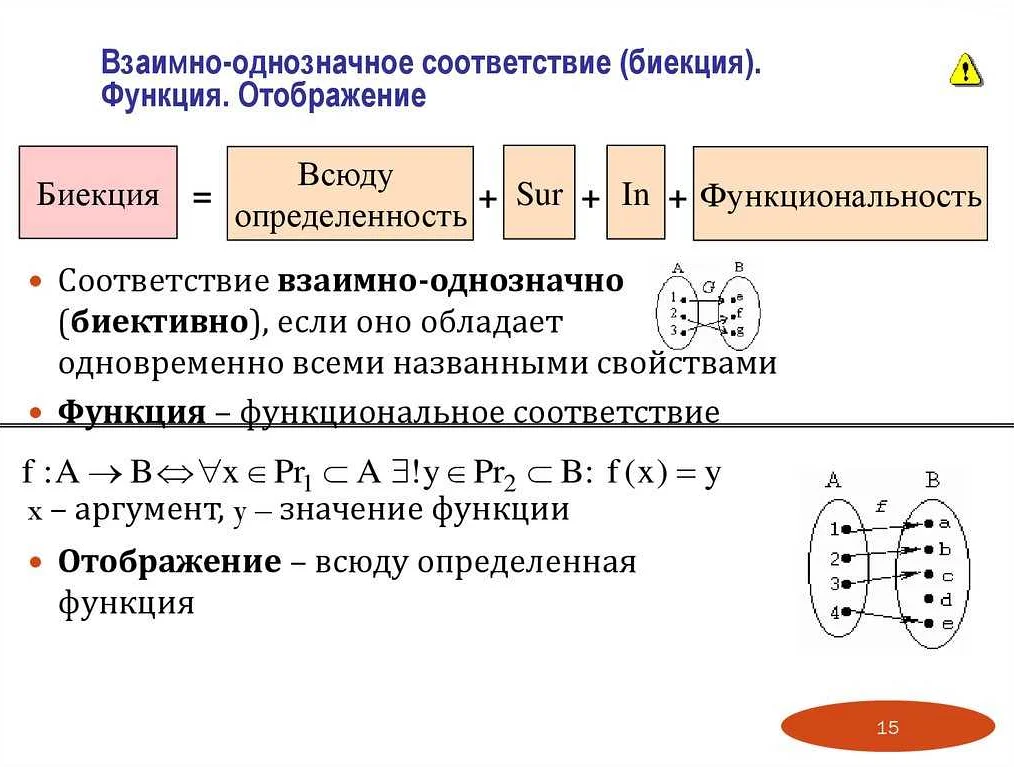



Соответствие в математике — это основной концепт, который используется для установления связи между двумя множествами. Оно определяет, что каждому элементу одного множества соответствует ровно один элемент второго множества, и наоборот. Это позволяет нам устанавливать отношения и связи между различными математическими объектами. Например, если мы рассматриваем множество всех студентов в университете и множество всех их курсов, то соответствие между этими множествами может быть установлено путем присвоения каждому студенту его регистрационного номера и соответствующего ему курса. Таким образом, мы можем установить отношение между каждым студентом и его курсом. В математике соответствие может быть представлено в виде таблицы, графа или формулы. Оно играет важную роль во многих областях математики, включая алгебру, геометрию и теорию множеств. Понимание соответствия позволяет нам решать различные задачи и формулировать математические модели. Таким образом, соответствие в математике является ключевым понятием, которое помогает нам понять и описать отношения между различными объектами. Это важный инструмент, который используется для развития и применения математических концепций и теорий.
Статья очень полезная и информативная. В ней хорошо объяснено понятие соответствия в математике. Я всегда думал, что соответствие это просто совпадение или сходство, но благодаря этой статье я узнал, что в математике это немного другое. Соответствие — это отношение между двумя множествами, где каждому элементу одного множества соответствует элемент другого множества. Примеры, которые приведены в статье, помогли мне лучше понять это понятие. Я теперь понимаю, что соответствие может быть однозначным, когда каждому элементу одного множества соответствует только один элемент другого множества, и многозначным, когда каждому элементу одного множества может соответствовать несколько элементов другого множества. Статья отлично дополнила мои знания в математике и помогла мне лучше понять это важное понятие. Большое спасибо автору за такую полезную статью!