Что обозначает в и на в математике

В математике предлоги ‘в’ и ‘на’ используются для обозначения различных концепций и отношений. Они могут указывать на пространственное расположение объектов, указывать находится ли объект внутри или снаружи другого объекта, обозначать диапазон значений или временной интервал, а также указывать на принадлежность или включение в группу. Узнайте, как правильно использовать эти предлоги в математическом контексте.

Математика – это строгая наука, которая использует специальные термины и символы для обозначения математических операций, отношений и понятий. Одним из таких терминов являются предлоги «в» и «на», которые имеют свое специфическое значение в контексте математических выражений и формул.

Предлог «в» в математике обычно используется для обозначения вхождения элемента в множество или совокупность. Например, если у нас есть множество всех натуральных чисел, то можно сказать, что число 5 «входит в» это множество. Это можно записать следующим образом: 5 ∈ N, где символ «∈» означает «принадлежит».

С другой стороны, предлог «на» в математике обычно используется для обозначения отношения между двумя объектами или операциями. Например, если у нас есть два числа a и b, то можно сказать, что число a «находится на» числе b. Это можно записать следующим образом: a ∩ b, где символ «∩» означает «находится на».

Примеры:

• Вхождение в множество: Единица «входит в» множество всех целых чисел: 1 ∈ Z.
• Отношение между числами: Число 3 «находится на» числе 5: 3 ∩ 5.

Таким образом, предлоги «в» и «на» в математике имеют свои специфические значения и используются для обозначения вхождения и отношений между объектами и операциями. Их правильное использование помогает более точно и ясно выражать математические идеи и концепции.

Что означает «в» и «на» в математике

В математике предлоги «в» и «на» часто используются для выражения отношений и связей между различными математическими объектами.

Предлог «в» обычно означает принадлежность объекта к множеству или нахождение внутри определенного пространства. Например:

• В множестве N — означает, что число является натуральным
• В трехмерном пространстве — означает, что объект находится внутри трехмерного пространства

Предлог «на» обычно означает отношение объекта к поверхности или плоскости. Например:

• На плоскости — означает, что точка лежит на плоскости
• На прямой — означает, что точка лежит на заданной прямой

Использование предлогов «в» и «на» в математике может быть различным и зависит от конкретного контекста и задачи.

Определение «в» в математике

Примеры:

1. Если рассматривать множество натуральных чисел, то число 2 входит в это множество, поэтому можно сказать, что 2 в множестве натуральных чисел.

2. Если рассматривать множество трехмерных геометрических фигур, то куб находится в этом множестве, поэтому можно сказать, что куб в множестве трехмерных геометрических фигур.

3. Если рассматривать область определения функции, то число 3 входит в эту область, поэтому можно сказать, что 3 в области определения функции.

Таким образом, предлог «в» в математике помогает указать принадлежность объекта к множеству или области.

Что значит «в» в математических формулах

Например, если у нас есть множество натуральных чисел {1, 2, 3, 4, 5}, то мы можем записать «2 в множестве натуральных чисел». Это означает, что число 2 является элементом данного множества.

Также символ «в» может использоваться для обозначения принадлежности точки к геометрической фигуре. Например, если у нас есть квадрат ABCD и точка E, то мы можем записать «точка E внутри квадрата ABCD». Это означает, что точка E находится внутри границ квадрата ABCD.

Символ «в» в математических формулах имеет важное значение для определения отношений между элементами множеств и геометрическими фигурами.

Примеры использования «в» в математике

В математике предлог «в» может использоваться в различных контекстах. Например:

1. Векторное пространство:

Векторное пространство — это абстрактное математическое понятие, которое описывает некоторую совокупность векторов, на которой определены операции сложения и умножения на число. Например, векторное пространство R^2 обозначает множество всех упорядоченных пар вещественных чисел (x, y), где x и y — координаты вектора.

2. Вероятность:

Вероятность — это числовая характеристика, описывающая степень уверенности в наступлении события. Вероятность события A обозначается как P(A) и может принимать значения от 0 до 1. Например, вероятность выпадения герба при подбрасывании монеты равна 0.5.

3. Взаимно простые числа:

Два числа называются взаимно простыми, если их наибольший общий делитель равен 1. Например, числа 3 и 4 являются взаимно простыми.

4. Векторное произведение:

Векторное произведение — это операция над векторами, результатом которой является вектор, перпендикулярный исходным векторам. Векторное произведение двух векторов a и b обозначается как a × b. Например, векторное произведение векторов (1, 0, 0) и (0, 1, 0) равно (0, 0, 1).

5. Внутреннее произведение:

Внутреннее произведение — это операция над векторами, результатом которой является скалярное значение. Внутреннее произведение двух векторов a и b обозначается как a · b. Например, внутреннее произведение векторов (1, 2) и (3, 4) равно 11.

Это лишь некоторые примеры использования предлога «в» в математике. Математика широка и разнообразна, поэтому предлог «в» может встречаться во множестве других математических понятий и формул.

Примеры использования «в» в алгебре

1. Использование «в» в обозначении множества:

В алгебре символ «в» может использоваться для обозначения принадлежности элемента множеству. Например, можно записать, что число 3 входит в множество натуральных чисел следующим образом: 3 ∈ N.

2. Использование «в» в операциях над множествами:

Символ «в» также используется для обозначения операций над множествами. Например, можно записать, что элемент x содержится в объединении двух множеств A и B следующим образом: x ∈ (A ∪ B).

3. Использование «в» в определении диапазона значений:

В алгебре символ «в» может использоваться для определения диапазона значений переменной. Например, можно записать, что переменная x принадлежит интервалу от 1 до 5 следующим образом: x ∈ [1, 5].

4. Использование «в» в матричных операциях:

Символ «в» также может быть использован в операциях с матрицами. Например, можно записать, что матрица A содержит элемент a в i-й строке и j-м столбце следующим образом: a ∈ A[i, j].

Это лишь некоторые примеры использования символа «в» в алгебре. Однако, в математике существует еще множество других контекстов, в которых этот символ может быть использован с различными значениями и обозначениями.

Примеры использования «в» в геометрии

В геометрии термин «в» используется для указания нахождения одной фигуры внутри другой. Например:

Прямоугольник «А» внутри прямоугольника «В»:

В данном случае, прямоугольник «А» полностью находится внутри прямоугольника «В». Это может быть полезно, например, для определения площади прямоугольника «А» в зависимости от площади прямоугольника «В».

Круг «А» внутри круга «В»:

Аналогично, круг «А» полностью находится внутри круга «В». Это может быть полезно, например, для определения площади круга «А» в зависимости от площади круга «В».

Треугольник «А» внутри треугольника «В»:

Треугольник «А» полностью находится внутри треугольника «В». Аналогично прямоугольнику и кругу, это может быть полезно для определения площади треугольника «А» в зависимости от площади треугольника «В».

Обратите внимание, что «в» указывает на полное нахождение одной фигуры внутри другой, без каких-либо пересечений.

Определение «на» в математике

В математике термин «на» используется для обозначения отношения между элементами двух множеств. Если элемент принадлежит одному множеству и находится на другом, то говорят, что он находится на втором множестве.

В примерах этого отношения можно увидеть, как «на» используется для обозначения пространственного положения объектов относительно друг друга. Например:

• Книга лежит на столе.
• Машина стоит на парковке.
• Мяч летит на футбольное поле.

В математическом контексте термин «на» может использоваться для обозначения различных отношений, таких как нахождение в некотором пространстве или отношение порядка. Например:

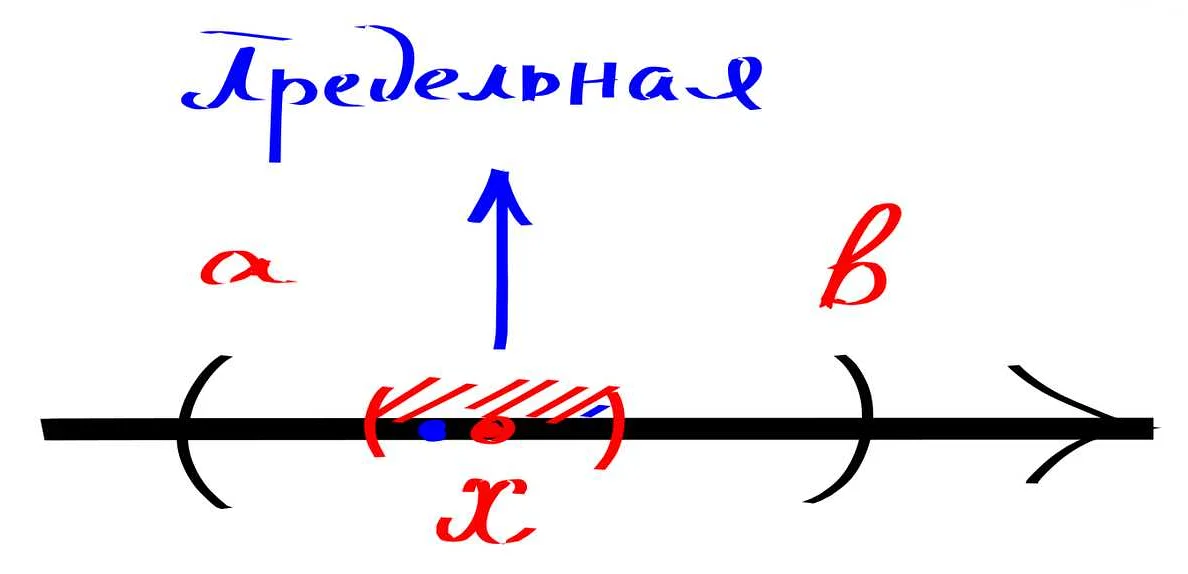
• Число 5 находится на числовой прямой между 4 и 6.
• Множество A содержит элементы, находящиеся на множестве B.
• Функция f(x) принимает на входе значение x и вычисляет значение на основе заданной формулы.

Использование термина «на» в математике может изменяться в зависимости от конкретного контекста и определения, но общая идея остается одной — обозначение отношения между элементами различных множеств.

Что значит «на» в математических формулах

В математических формулах термин «на» используется для обозначения различных отношений между объектами. В зависимости от контекста, значение этого предлога может быть разным.

1. Отношение включения: предлог «на» может обозначать отношение включения, когда одно множество содержится в другом. Например, если A на B, это означает, что множество A содержится в множестве B.

2. Отношение операции: предлог «на» может указывать на операцию, выполняемую над объектами. Например, a + b означает, что выполняется операция сложения между a и b.

3. Отношение зависимости: предлог «на» может указывать на зависимость одного объекта от другого. Например, функция f на x означает, что значение функции f зависит от значения переменной x.

Таким образом, значение предлога «на» в математических формулах зависит от контекста и может указывать на отношение включения, операцию или зависимость между объектами.

Примеры использования «на» в математике

В математике предлог «на» используется в различных контекстах, чтобы указать на отношение между объектами. Вот некоторые примеры:

1. Умножение на число

Мы можем сказать, что число «а» умножается на число «b», что записывается как а * b. Это означает, что мы берем число «а» и увеличиваем его в «b» раз. Например, если а = 2 и b = 3, то а * b = 2 * 3 = 6.

2. Деление на число

Аналогично, мы можем сказать, что число «а» делится на число «b», что записывается как а / b. Это означает, что мы делим число «а» на равные части, каждая из которых равна числу «b». Например, если а = 10 и b = 2, то а / b = 10 / 2 = 5.

3. Функция на множестве

В математическом анализе функция «f» может быть определена на множестве «X». Это означает, что для каждого элемента «x» из множества «X» существует соответствующий элемент «y» из множества «Y», такой что f(x) = y. Например, функция f(x) = x^2 определена на множестве всех действительных чисел.

4. Отображение на графике

Когда мы строим график функции, мы часто используем ось «x» и ось «y». Мы можем сказать, что значение «x» отображается на значение «y». Например, если у нас есть уравнение y = x^2, мы можем отобразить каждое значение «x» на соответствующее значение «y» на графике.

Использование предлога «на» в математике помогает нам устанавливать связь между различными объектами и операциями, что позволяет нам лучше понять и работать с математическими концепциями.

Примеры использования «на» в анализе

Предлог «на» в математике может использоваться для обозначения различных концепций и операций в анализе.

Один из примеров использования «на» в анализе — это обозначение операции «производная на функции». Если дана функция f(x), то ее производная на точке x обозначается как f'(x) или df/dx. Это позволяет найти скорость изменения функции в данной точке.

Другой пример — это обозначение интеграла на функции. Интеграл на функции f(x) обозначается как ∫f(x)dx. Это позволяет найти площадь под кривой функции в заданном интервале или найти значение определенного интеграла.

Также, предлог «на» может использоваться для обозначения ограниченности функции на множестве. Например, функция f(x) может быть ограничена на множестве A, что обозначается как f(x) на A.

Выводы, сделанные с использованием «на» в анализе, могут помочь в решении различных задач и проблем в математике.

Видео по теме:

Что означает «в» и «на» в математике?

В математике «в» и «на» могут использоваться для указания местоположения объектов. Например, если говорить о графике функции, то «в» может обозначать, что точка находится внутри графика, а «на» — что она находится на самом графике.

Можно ли использовать «в» и «на» в математике для обозначения действий?

Нет, «в» и «на» в математике обычно используются для указания местоположения объектов, а не для обозначения действий. Для обозначения действий используются другие математические символы и операторы.

Как определить, когда использовать «в» и когда использовать «на» в математике?

Определить, когда использовать «в» и когда использовать «на» в математике можно, исходя из контекста и смысла фразы. Если речь идет о местоположении точки внутри объекта, то используется «в». Если речь идет о местоположении точки на поверхности объекта или на графике функции, то используется «на».